-
Nucleon and nuclear matter (nucleon systems, such as nucleus and neutron star) contains 99% mass of the visible universe. However, their internal structures are not fully understood, such as where does the nucleon spin come from[1], and how nuclear medium environment modifies the quark and gluon distributions in the nucleon[2] Nucleon, referred as a proton or a neutron, is a not point-like particle, but a confined system around 1 fm (1/0.2
${\rm GeV} ^{-1} $ ). Under high energy collisions, the interaction happens on quarks or gluons inside the nucleon instead of the whole nucleon. To interpret the inner structure of hadron and the strong interaction system, collinear parton distribution is the classic and powerful tool.Parton distribution function (PDF) is the parton density distribution over
$ x $ , where the variable$ x = p/P $ is defined as the momentum fraction carried by the parton.$ p $ denotes the light-front momentum of the parton;$ P $ denotes the light-front momentum of the proton. In quantum chromodynamics (QCD) theory, PDFs depend on the energy scale of a measurement. For deep inelastic scattering (DIS), PDF varies with$ Q^2 = -q^2 $ defined as the minus momentum square of the virtual photon ($ Q^2 $ is the resolution power of the photon probe). Within the factorization theorem, many high energy processes involving hadrons can be calculated using PDFs of the “soft” part and the perturbative calculation of the “hard” part.Nowadays, there are a lot of global analyses of PDFs[3–5]. However complicated function forms are used to model the initial parton distribution functions with a lot of free parameters (~20). So many free parameters increase the uncertainties of PDFs. The other problem is that there is no connection between the quark model and the parton distribution functions probed at
$ Q^2 $ . For nuclear PDFs, the uncertainties of sea quark and gluon distributions are even larger[6-7], for the nuclear effects are so intricate that there is no commonly accepted model to describe the nuclear medium corrections. Reducing the uncertainties of nuclear PDFs is challenging and important.A much simple way to reduce the uncertainties of the initial parton distributions is to use the dynamical parton model which parameterize the input PDFs at an extremely low scale
$ Q_0^2 $ where all sea quark and gluon distributions are zero[8] ($ Q_0^2 $ is the initial scale for the perturbative QCD evolution). In this approach, only three free parameters are used to describe the valence quark distributions. The other advantage is that at extremely low$ Q_0^2 $ , all nuclear medium corrections are performed only to the three valence quark distributions, which reduces the uncertainties of the nuclear sea quark and gluon distributions greatly. IMParton for nucleon PDFs[9] and nIMParton for nuclear PDFs[10] show some interesting results of the dynamical parton approach, and some successful applications. In our previous works, we used a leading order$ \alpha_{\rm s} $ without any nonperturbative effects. It is argued that at extremely low$ Q^2 $ ($ <0.5 $ GeV2), the strong coupling constant is saturated instead of going to infinity[11]. We also had estimated the valence quark distributions of proton at$ Q_0^2 $ using a maximum entropy method (MEM)[12]. In this work, we try to use the saturated strong coupling$ \alpha_{\rm s} $ and the valence distributions from MEM as the nonperturbative input.Reliable nuclear parton distributions are indispensable for the study of parton energy loss during the process of a parton going through the nuclear matter (a nucleus). The European Muon Collaboration (EMC) effect, nuclear shadowing and the parton energy loss make the per-nucleon Drell-Yan cross-section of p-A smaller than that of p-D. Therefore, to disentangle the parton energy loss from the nuclear modifications on nuclear PDFs, reasonable and precise nuclear PDFs are needed. The dynamical parton model introduces no uncertainty of parametrization of sea quark and gluon distributions, which can give a crucial implication of the parton energy loss in cold nuclear matter.
-
The
$ Q^2 $ -dependence of PDFs is governed by the QCD dynamics, namely the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) equations with parton splitting processes in leading logarithmic approximation[13]. The$ Q^2 $ -dependence comes from summing the leading logarithmic corrections and physically means that the DIS with a photon probe of virtuality$ Q^2 $ corresponds to the scattering of that virtual photon off a quark of transverse size$ 1/Q $ . With the increasing of$ Q^2 $ , the photon probe can resolve more partons of smaller size.At low
$ Q^2 $ , the parton size is big and the wave functions of partons overlaps. Considering that the running strong coupling is big at low$ Q^2 $ , the parton-parton recombination processes should not be ignored for this case. Toward small$ x $ , the densities of partons go up very rapidly with no limit from the parton splitting processes. Under the extremely high density, two-parton fusion process happens with a significant probability in the small$ x $ region, and it is supposed to cease the increase of the cross-section near the unitarity limit. Gribov, Levin and Ryskin (GLR)[14] first introduce the theoretical prediction of the parton-parton interaction for the semi-hard process, and further developed by Mueller and Qiu (MQ)[15], and Zhu, Ruan, Shen (ZRS)[16] with different calculation techniques.We are motivated to investigate the simplest origin of partons at an extremely low
$ Q^2 $ , therefore in this paper, DGLAP equations with two-parton fusion corrections are applied to evolve the PDFs over$ Q^2 $ . So far, ZRS have considered all the fusion probabilities for gluon-gluon, quark-gluon and quark-antiquark. Our previous study shows that the gluon-gluon recombination correction is dominant, as the gluon density is much larger than the quark density at small$ x $ . So we use the DGLAP equations with only the two-gluon recombination correction[8, 9], as following,$$ Q^2\frac{{\rm{d}}xf_{q_i^{\rm{NS}}}(x,Q^2)}{dQ^2} = \frac{\alpha_{\rm s}(Q^2)}{2\pi}P_{qq}\otimes f_{q_i^{\rm{NS}}}, $$ (1) for the flavor non-singlet quark distributions
$ f_{q_i^{\rm{NS}}} $ ,$$ \begin{split} &Q^2\frac{{\rm{d}}xf_{\bar{q}_i^{\rm{DS}}}(x,Q^2)}{{\rm{d}}Q^2} = \frac{\alpha_{\rm s}(Q^2)}{2\pi}\big[P_{qq}\otimes f_{\bar{q}_i^{\rm{DS}}}+P_{qg}\otimes f_g\big]-\\&\quad \frac{\alpha_{\rm s}^2(Q^2)}{4\pi R^2Q^2}\int\nolimits_x^{1/2} \frac{{\rm{d}}y}{y}xP_{gg\to \bar{q}}(x,y)\big[yf_g(y,Q^2)\big]^2+\\ &\quad\frac{\alpha_{\rm s}^2(Q^2)}{4\pi R^2Q^2}\int\nolimits_{x/2}^{x}\frac{{\rm{d}}y}{y}xP_{gg\to \bar{q}}(x,y)\big[yf_g(y,Q^2)\big]^2, \\[-14pt] \end{split}$$ (2) for the dynamical sea quark distributions
$ f_{\bar{q}_i^{\rm{DS}}} $ , and$$ \begin{split}& Q^2\frac{{\rm{d}}xf_{g}(x,Q^2)}{{\rm{d}}Q^2} = \frac{\alpha_s(Q^2)}{2\pi}\big[P_{gq}\otimes \Sigma+P_{gg}\otimes f_g\big]-\\&\quad \frac{\alpha_{\rm s}^2(Q^2)}{4\pi R^2Q^2}\int\nolimits_x^{1/2} \frac{{\rm{d}}y}{y}xP_{gg\to g}(x,y)\big[yf_g(y,Q^2)\big]^2+\\ &\quad\frac{\alpha_{\rm s}^2(Q^2)}{4\pi R^2Q^2}\int\nolimits_{x/2}^{x}\frac{{\rm{d}}y}{y}xP_{gg\to g}(x,y)\big[yf_g(y,Q^2)\big]^2, \end{split} $$ (3) for the gluon distribution
$ f_g $ , where the factor$ 1/(4\pi R^2) $ is from the normalization of the two-parton densities, and$ R $ is the correlation length of the two interacting partons.$ R $ is a little smaller than the hadron radius.$ \Sigma $ in Eq. (3) is defined as$ \Sigma(x,Q^2)\equiv \sum_jf_{q^{\rm{NS}}_j}(x,Q^2)+\sum_i\big[f_{q^{\rm{DS}}_i}(x,Q^2)+f_{\bar{q}^{\rm{DS}}_i}(x,Q^2)\big] $ . The splitting kernels of the linear terms are given by DGLAP equations, and the recombination kernels of the nonlinear terms are written as[16],$$ \begin{split} &P_{gg\to g}(x,y) = \\ &\frac{9}{64}\frac{(2y-x)(72y^4-48xy^3+140x^2y^2-116x^3y+29x^4)}{xy^5},\\& P_{gg\to q}(x,y) = \\& P_{gg\to \bar{q}}(x,y) = \frac{1}{96}\frac{(2y-x)^2(18y^2-21xy+14x^2)}{y^5}. \\[-13pt] \end{split}$$ (4) The terms which have the squares of parton distributions are the nonlinear two-parton recombination corrections. At small
$ x $ , partons from different nucleons also can combine into one parton. Therefore, for the system of nucleons (cold nuclear matter), two-parton recombinations are enhanced. -
The running coupling constant
$ \alpha_{\rm s} $ is a fundamental parameter of perturbative QCD, and it depends on the$ Q^2 $ scale which describes the momentum exchange during the interaction process. In leading order, Glück, Reya and Vogt (GRV) use the following running strong coupling,$$ \frac{\alpha_{{\rm s},{\rm{LO}}}(Q^2)}{4\pi} = \frac{1}{\beta_0\ln(Q^2/\varLambda^2)}, $$ (5) in which
$ \beta_0 = 11-2n_f/3 $ and$ \varLambda^{3,4,5,6}_{\rm{LO}} = 204 $ , 175, 132, 66.5 MeV[3].$ n_{\rm f }$ is the number of quark flavors involved. For the$ \alpha_{\rm s} $ matchings,$ m_c = 1.4 $ GeV,$ m_b = 4.5 $ GeV,$ m_t = 175 $ GeV are used as the masses of the heavy quarks. This strong coupling is determined by the global fit to the deep inelastic scattering data in a wide$ Q^2 $ range.The coupling constant in Eq. (5) goes to infinity approaching the cutoff
$ \varLambda^2 $ . The nonperturbative effect should be considered at low$ Q^2 $ . In Dyson-Schwinger equation (DSE), the quark and gluon gain the effective masses from QCD dynamics. Based on DSE, the strong coupling from the ghost-vertex with the effective masses for gluon and quark is written as[11],$$ \begin{split}\alpha_{{\rm s},{\rm{DSE}}}(Q^2)& = \frac{\varLambda^2}{\varLambda^2+Q^2} \times \\&\left[ 2.972+\frac{4\pi}{\beta_0}\Big( \frac{1}{\ln(Q^2/\varLambda^2)}+\frac{\varLambda^2}{\varLambda^2-Q^2} \Big) \frac{Q^2}{\varLambda^2} \right], \end{split} $$ (6) where
$ \varLambda^2 = 0.034 $ to match GRV's$ \alpha_{\ rm s} $ at the charm quark threshold$ Q^2 = 1.96 $ GeV2. This DSE strong coupling is used in this work, and shown in Fig. 1. -
In dynamical parton model, the QCD evolution starts at quite a low
$ Q_0^2 $ where the sea quark and gluon distributions are small (less than$ \sim 30 $ % in total). Applying DGLAP equations with parton-parton recombination corrections, we extend the dynamical parton model to an extremely low starting scale$ Q_0^2 $ , with no sea quarks and no gluons at the scale. In our model, the sea quarks and gluons are purely from the DGLAP evolution, which is illustrated in Fig. 2.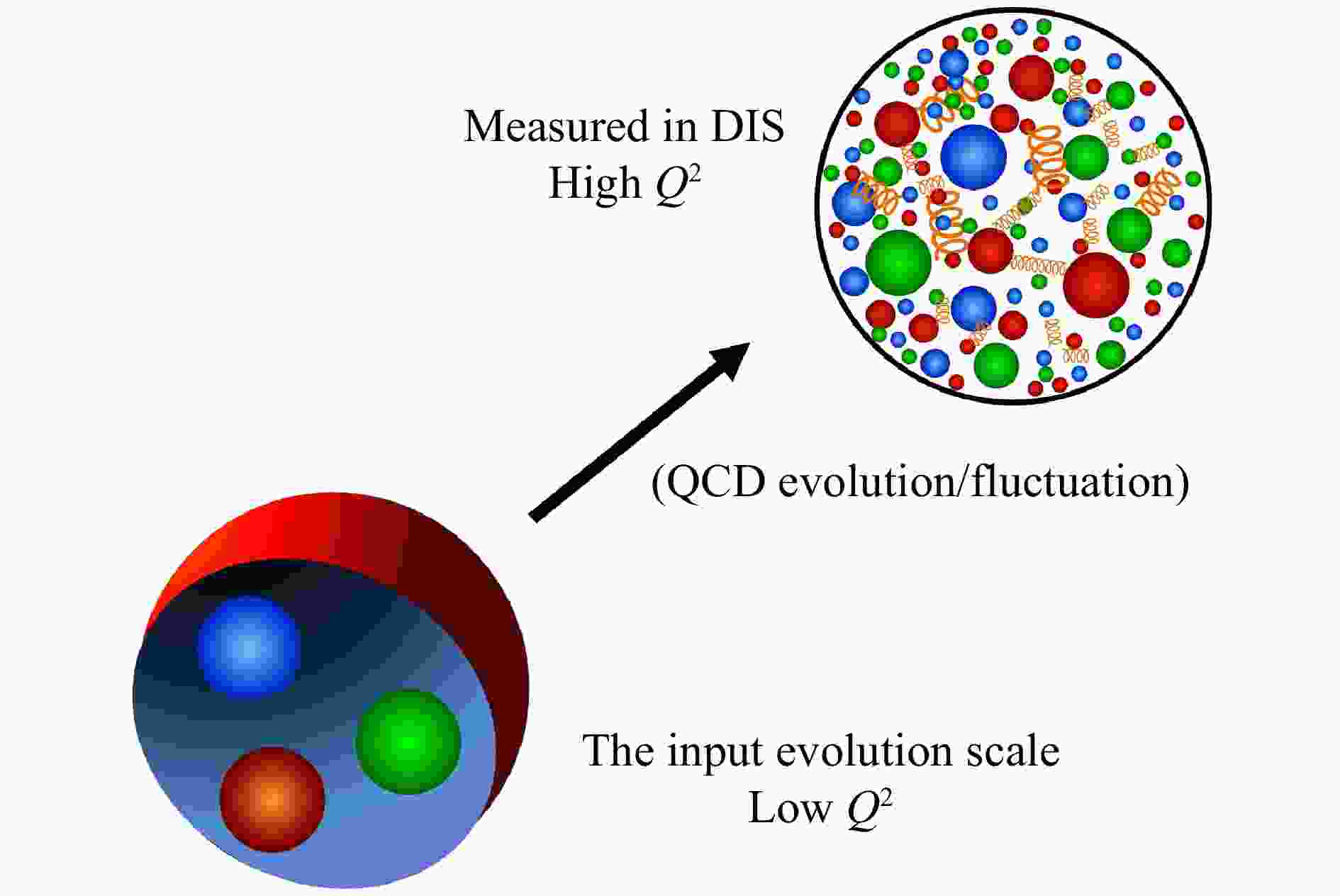
Figure 2. (color online) In our model, all the sea quarks and gluons are generated from the QCD fluctuations.
For the nonperturbative input, we have composed the initial parton distributions of mere three valence quarks from the maximum entropy method, which is given as[12],
$$ \begin{split}& xu_v(x,Q_0^2) = 4.589x^{1.095}(1-x)^{1.000}, \\& xd_v(x,Q_0^2) = 7.180x^{1.427}(1-x)^{2.456}, \end{split}$$ (7) where
$ u_v $ is the up valence quark distribution,$ d_v $ is the down valence quark distribution, and$ x $ is the momentum fraction of the quark. Do the dynamical parton distributions from the radiations of the initial valence quarks agree with the experimental measurements? In this work, we answer the question by evolving the input of only three valence quarks from MEM [Eq. (7)] with the parton-parton recombination corrected DGLAP equations. -
Generally, nuclear medium modifications have four types: the Fermi motion correction (
$ x>0.7 $ region), the EMC effect ($ 0.3<x<0.7 $ ), the anti-shadowing (region of$ x\sim 0.1 $ ), and the nuclear shadowing ($ x<0.05 $ region). Fermi motion affects the nucleon structure greatly only near the elastic scattering kinetic ($ x\sim 1 $ ). In our previous analysis, EMC effect and anti-shadowing effect can be explained with the nucleon swelling model. The nucleon size is enlarged due to the modification by the nucleons around. The width of the spatial distribution of quarks in nuclei is bigger. According to Heisenberg uncertainty principle, the width of momentum distribution of quarks in nuclei becomes narrower, which is shown in Fig. 3[17]. Based on the three valence quark distributions of free proton, we can calculate the three valence quark distributions of the proton in nuclear matter, as long as we know how much the nucleon size increased.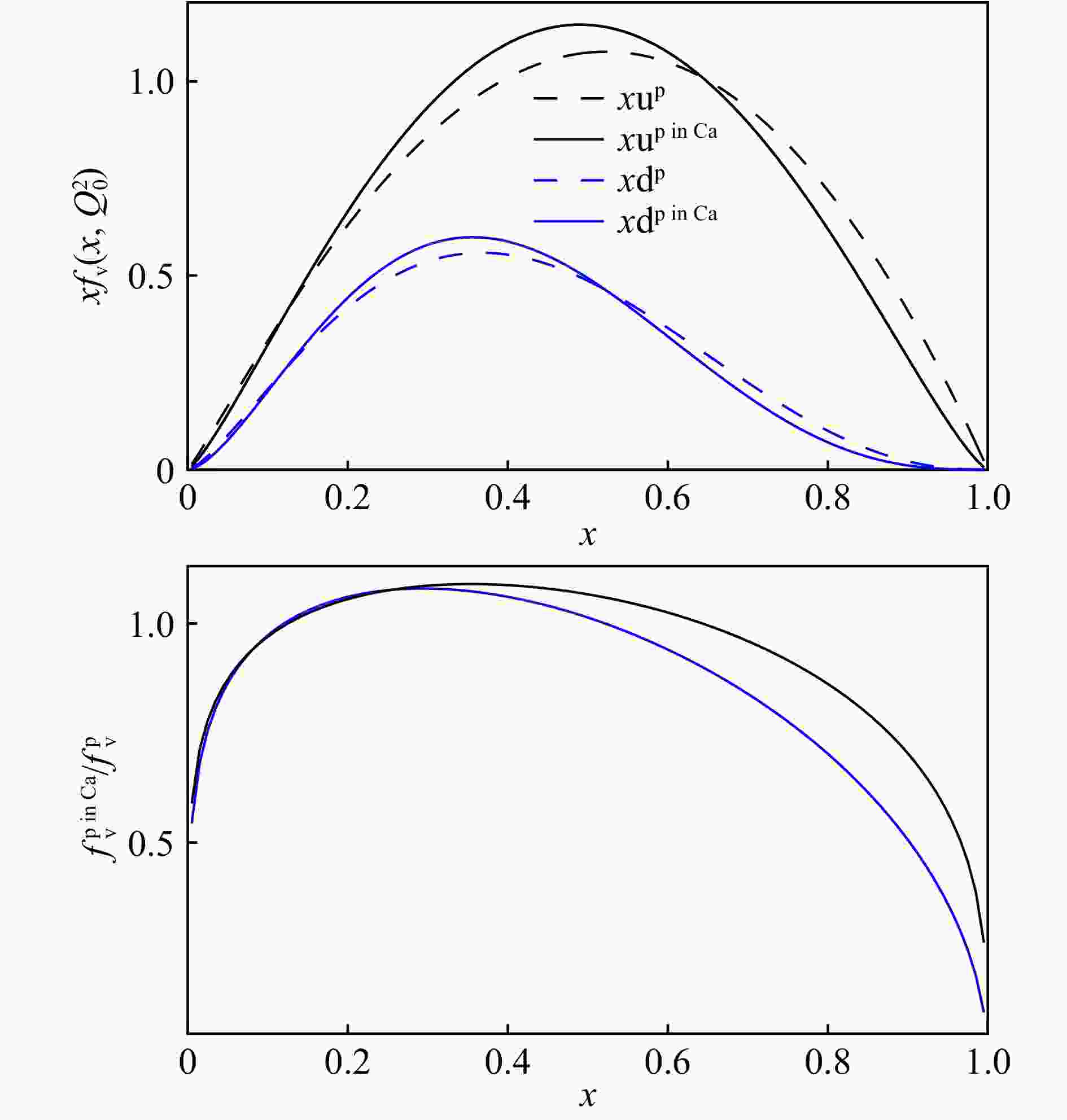
Figure 3. (color online) The initial valence quark distributions of the free proton and the bound proton (in 40Calcium). The width of the nuclear valence momentum distribution becomes narrower due to the nucleon swelling in nuclear medium.
Our previous study shows that the magnitude of the EMC effect is linearly correlated with the modified binding energy with the Coulomb contribution and the pairing contribution removed,
$B^{\rm{mod}}/A = (B-B^{\rm coul.}-B^{\rm pairing})/A$ [18]. Hence we assume the nucleon swelling$ \delta_A $ scales with the modified binding energy per nucleon,$$ \delta_A = \frac{R_p^A}{R_p}-1 = \alpha \times \frac{B^{\rm{mod}}}{A}, $$ (8) in which
$ \alpha $ is a parameter.$ \alpha $ describes the magnitude of nucleon radius modification in the nuclear matter.To model the nuclear shadowing is easy, as the shadowing effect is proportional to the nuclear size
$ A^{1/3} $ . In our model, the shadowing effect comes from the enhancement of parton-parton recombination process. Therefore the nonlinear terms in Eqs. (1, 2, 3) should be multiplied by an enhancement coefficient$ A_{\rm{shadowing}} $ , which is modeled as[10],$$ A_{\rm{shadowing}} = 1+\beta \times (A^{1/3}-1), $$ (9) in which
$ \beta $ is a parameter.$ \beta $ describes the magnitude of nuclear shadowing effect.In all, we can calculate the nuclear parton distributions with only two free parameters, in the dynamical parton model.
-
With the pure valence quark input (Eq. (7)), we obtained the starting scale
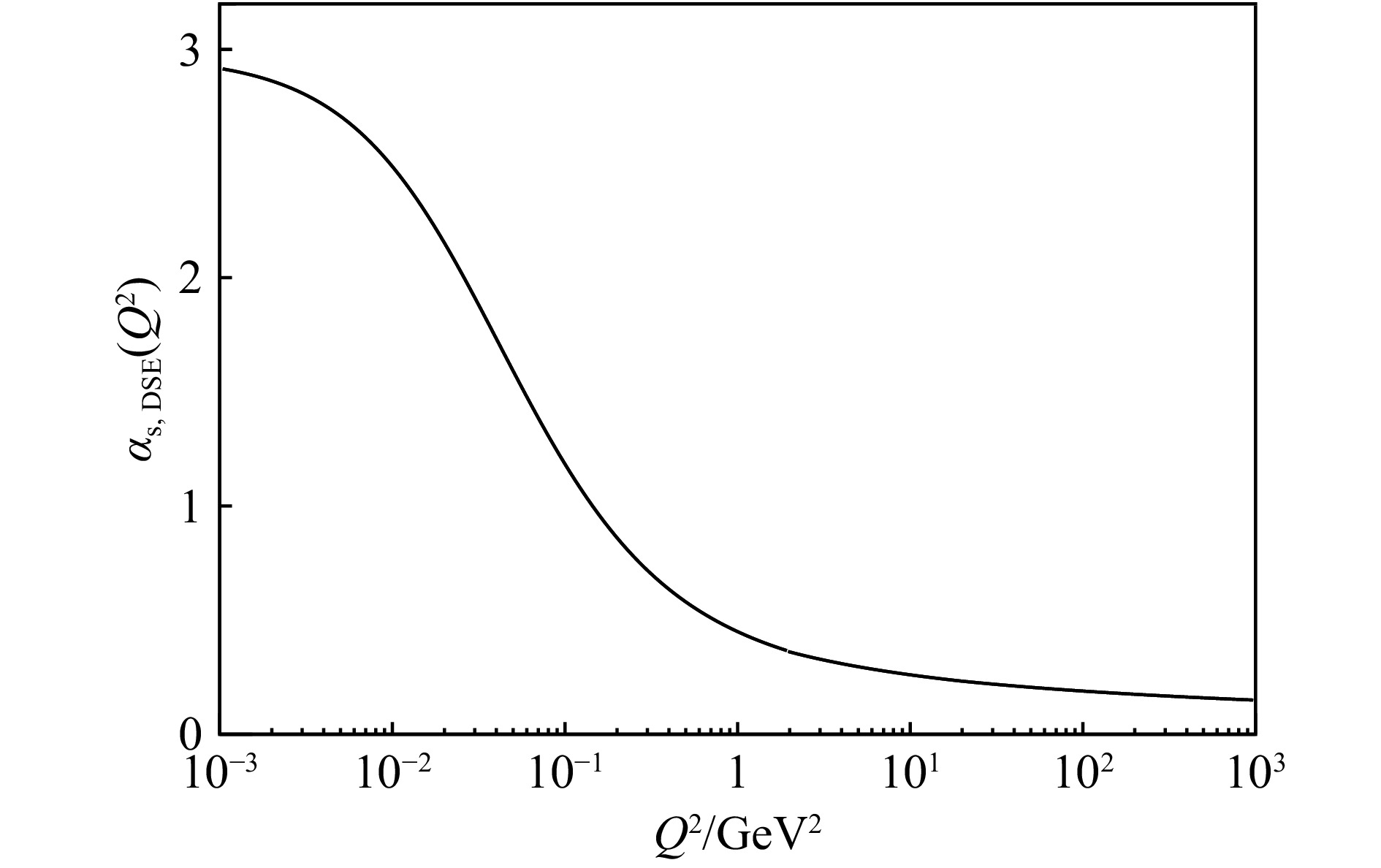
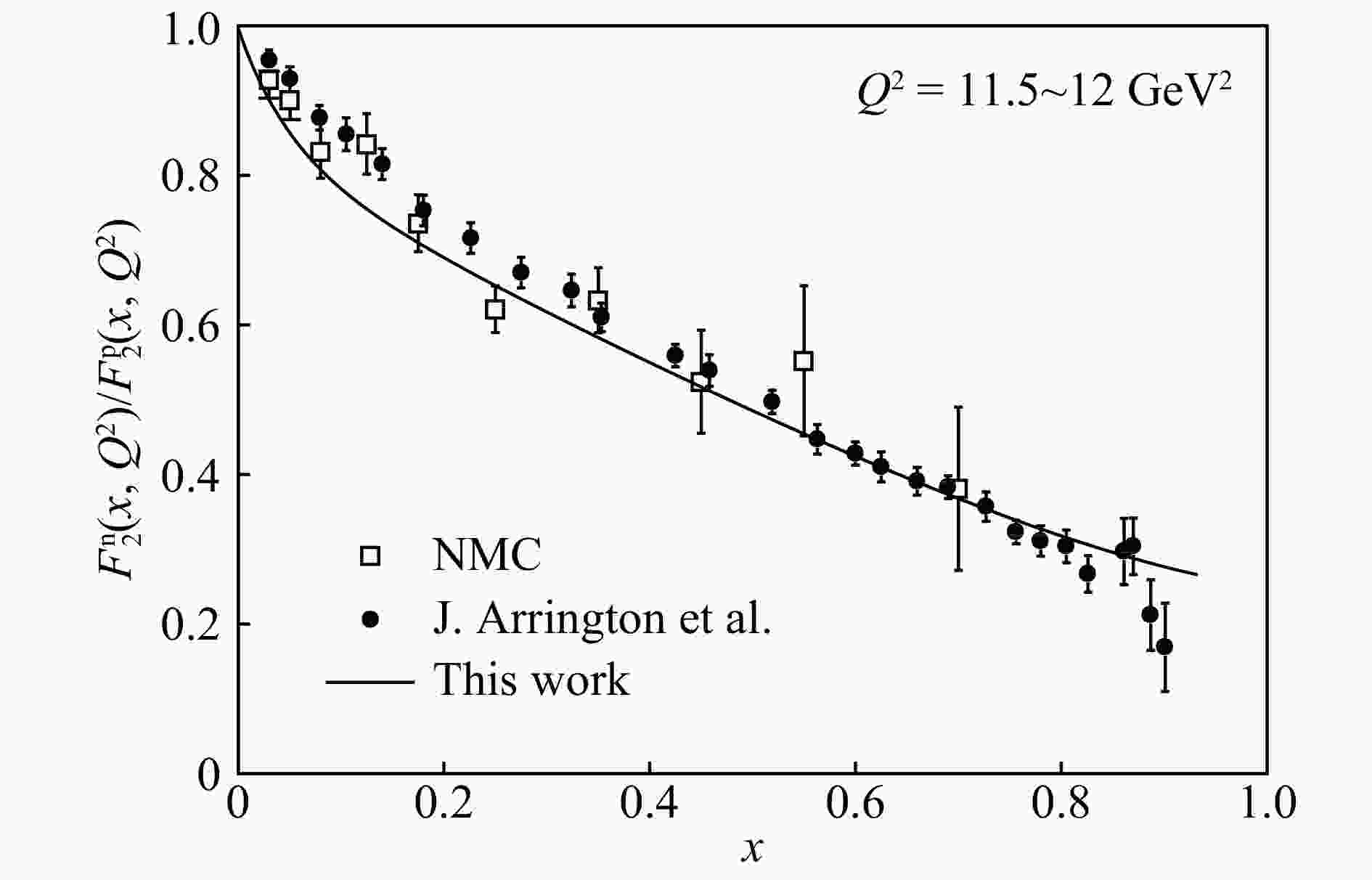
$ Q_0^2 $ to be 0.046 4 GeV2. The parton-parton correlation length$ R = 3.61 $ GeV–1 is taken from the previous study[9]. The proton structure function$ F_2 $ at small$ x $ is the product of sea quark distributions and Wilson coefficients. In Fig. 4, our predictions based on the dynamical sea quarks agree with the measurement at small$ x $ . Fig. 5 shows the predicted$ F_2 $ at large$ x $ compared with the experimental data. The ratio of neutron structure function and proton structure function is sensitive to valence quark distributions. Our predictions for the ratio$ F_2^{\rm n}/F_2^{\rm p} $ and the ratio$ d_v/u_v $ are shown in Fig. 6 and Fig. 7, respectively. The valence quark distributions at high$ Q^2 $ are consistent with the experiments.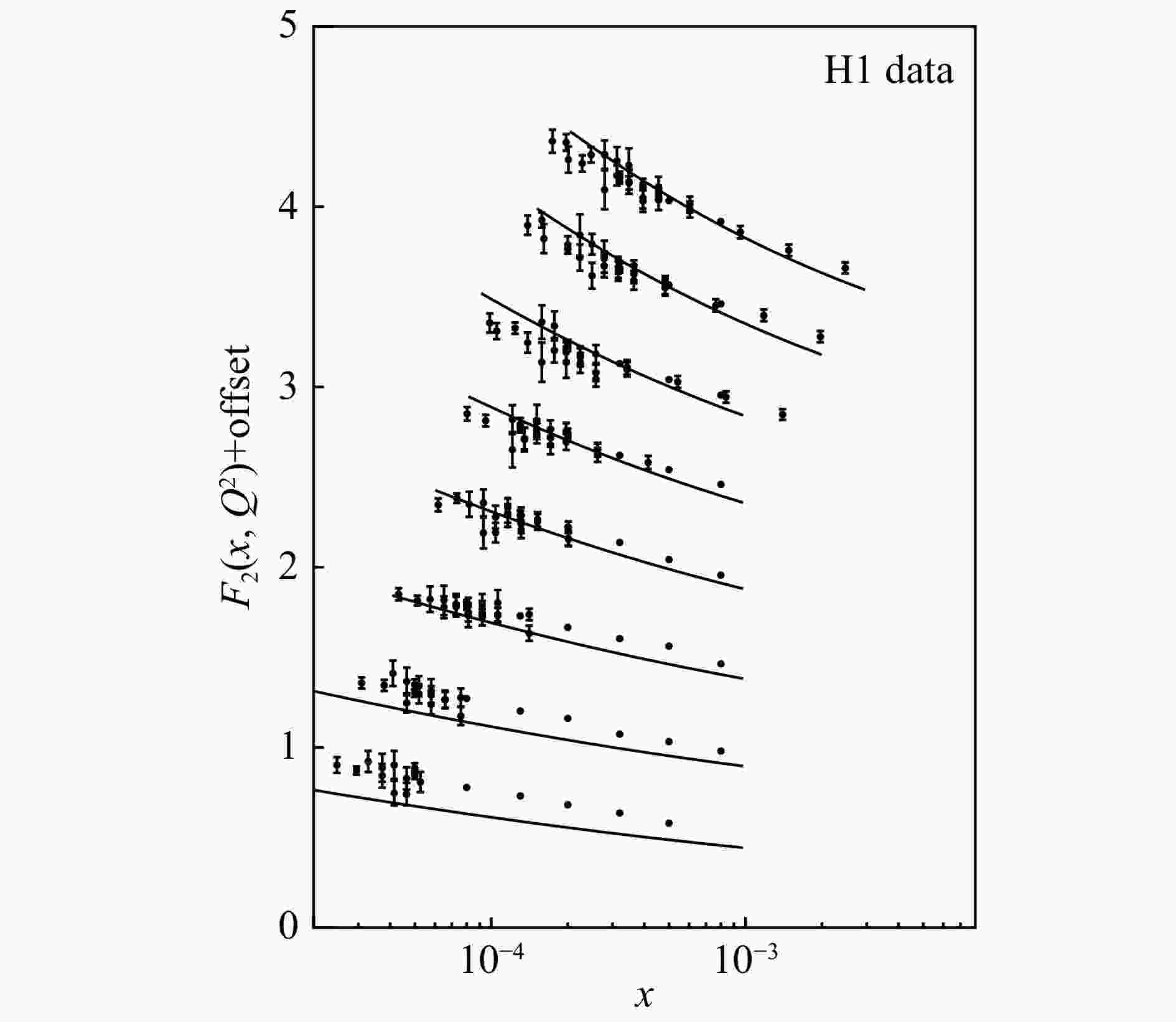
Figure 4. Comparisons of the predictions from the dynamical parton model with the proton structure function measurements by H1 collaboration[19].

Figure 5.
$Q^2$ -dependence of the predicted proton$F_2$ at large$x$ based on the dynamical parton model, compared with the experiments[20]. -
To depict the nuclear dependence of nucleon swelling,
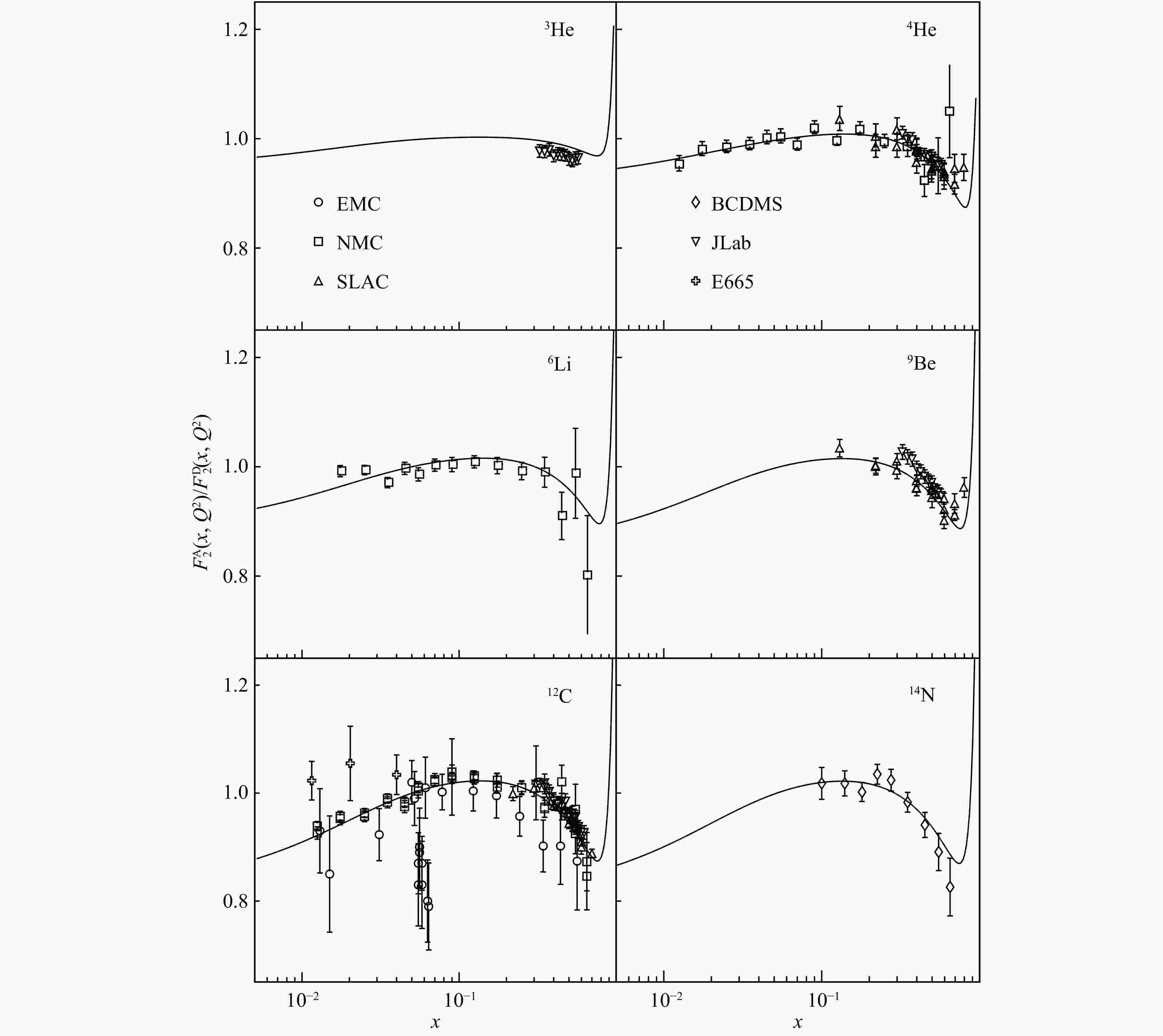
$ \alpha $ in Eq. (8) is determined to be 0.005 08, to match the observed nuclear EMC effect. To depict the nuclear dependence of parton-parton recombination enhancement,$ \beta $ in Eq. (9) is determined to be 0.296. With only these two parameters, we can generate the nuclear parton distribution functions in the dynamical parton model. The nuclear PDFs are usually demonstrated by the structure function ratios, which are precisely measured in experiments. The predictions of the nuclear medium corrections on$ F_2 $ are shown in Fig. 8 and Fig. 9. The EMC effect in the range$ 0.3<x<0.7 $ and the nuclear shadowing effect at$ x\lesssim 0.1 $ are successfully explained with the dynamical parton model.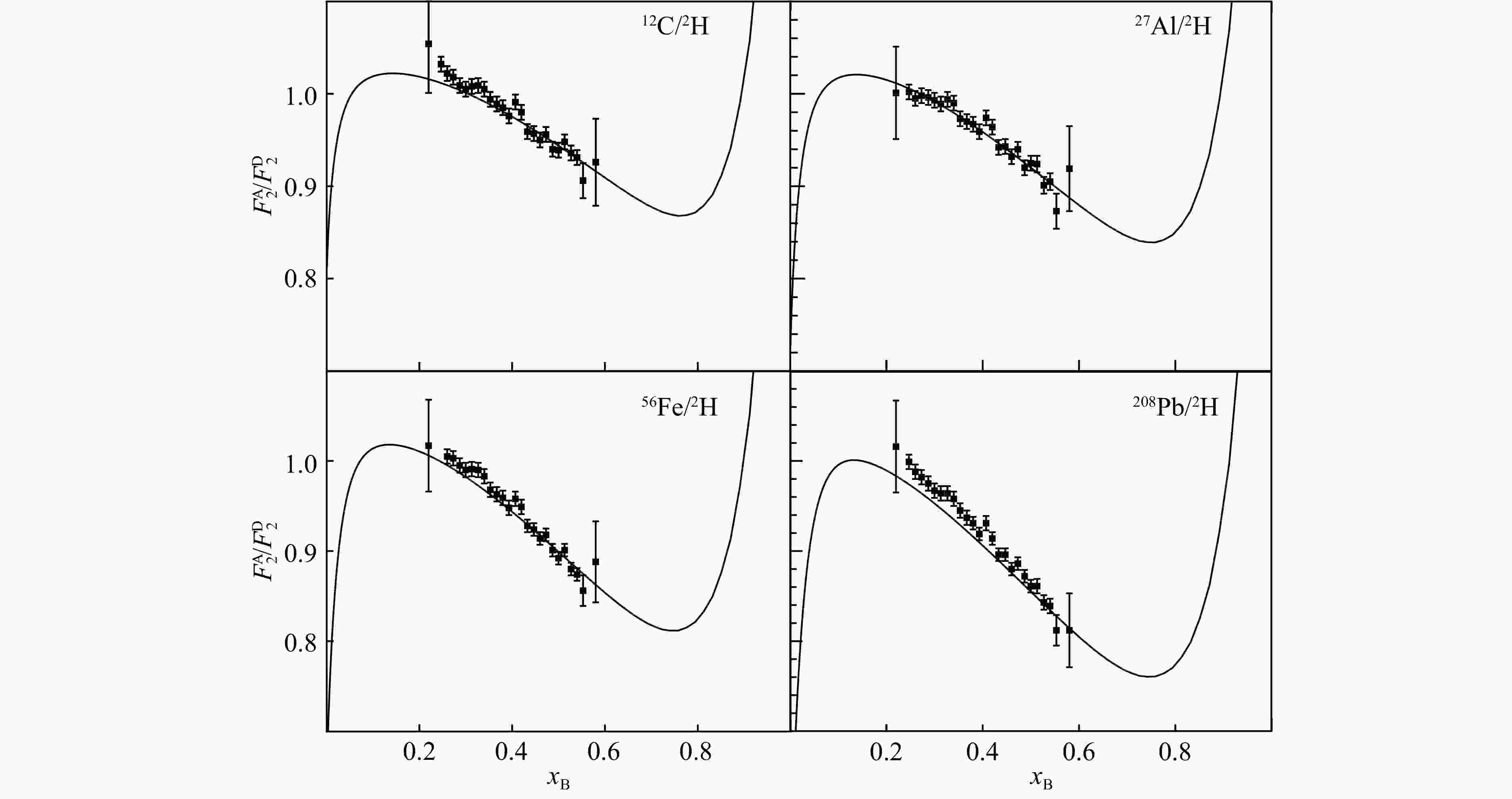
Figure 8. The predicted nuclear structure function ratios from the nuclear dynamical parton distributions compared with the experimental data[25], for some heavy nuclei, at
$Q^2 = 2~{\rm GeV}^2$ . -
Drell-Yan (DY) process describes the inclusive production of a lepton-antilepton pair when two hadronic matter collide together. DY process is on the parton level and expressed with a simple formula
$ q\bar{q}\to \gamma^* \to l\bar{l} $ . One quark from one incoming hadron and one antiquark from the other incoming hadron annihilate into one virtual photon which sequently decays into a pair of lepton and antilepton. In the DY process of p-A collision, the quark in the projectile proton possibly loses some energy propagating in the nuclear matter before the annihilation with an antiquark in the nuclear target. To confirm the quark energy loss passing through the nucleus is not easy, for EMC effect and nuclear shadowing give the same feature of quark energy loss in the experiment. In order to separate the parton energy loss from the nuclear modifications on PDFs, we need the nuclear PDFs which are strictly constrained by theory. The dynamical nuclear PDFs can be applied to this aim.In theory, there are two models describing the parton energy loss in nucleus. Model-1: parton energy loss is proportional to the penetrating length in nuclear matter (
$ \propto L $ ). Based on QCD bremsstrahlung and the uncertainty principle of quantum mechanic, Brodsky and Hoyer (BH) set an upper bound of the energy loss, which is 0.5 GeV/fm[32]. Model-2: parton energy loss is proportional to the square of the penetrating length in nuclear matter ($ \propto L^2 $ )[33–35]. Baier, Dokshitzer, Mueller, Peigné, and Schiff (BDMPS) argue that both the number of radiated gluons and the transverse momentum$ k_T $ of the gluon grow with$ L $ , so that the parton energy loss varies as$ \propto L^2 $ . For cold nuclear matter, they estimate the energy loss as 0.02~0.15 GeV/fm2[34].In leading order, the differential cross-section of DY process can be easily calculated in the parton model, which is derived as,
$$ \frac{{\rm{d}}^2\sigma}{{\rm{d}}x_1{\rm{d}}M} = K\frac{4\pi\alpha^2}{9M^2}\sum\limits_{q}e_q^2 \big[q_{1}(x_1)\bar{q}_{2}(x_2) + \bar{q}_{1}(x_1)q_{2}(x_2)\big], $$ (10) where “1” and “2” label the two colliding hadrons,
$ M $ is the invariant mass of the final di-lepton, and$ x_i $ is the quark momentum fraction of the colliding hadron. Due to the parton energy loss, we need to implement the momentum fraction correction$ \Delta x_1 $ for the projectile parton. According to model-1 of parton energy loss, we have$$ \Delta x_1 = \frac{\Delta E}{E_{\rm p}} = -\frac{\kappa_1 L}{E_{\rm p}}, $$ (11) where
$ \kappa_1 $ is a free parameter. According to model-2 of parton energy loss, we have$$ \Delta x_1 = \frac{\Delta E}{E_{\rm p}} = -\frac{\kappa_2 L^2}{E_{\rm p}}, $$ (12) where
$ \kappa_2 $ is a free parameter. The average passing length is calculated as$ L = \frac{3}{4}R_A = \frac{3}{4}(1.2A^{1/3}) $ fm for nucleus[34].By fitting to E772[36] and E866[37] data,
$ \kappa_1 $ and$ \kappa_2 $ are obtained to be$ 0.39\pm 0.19 $ GeV/fm and$ 0.07\pm 0.04 $ GeV/fm2. The qualities of the fits are$ \chi^2/N = 0.89 $ and$ \chi^2/N = 0.88 $ for model-1 and model-2 respectively. With no parton enery loss,$ \chi^2/N $ is 0.98. Using dynamical nuclear PDFs, we find that the values of$ \kappa_1 $ and$ \kappa_2 $ are consistent with BH's and BDMPS' estimations respectively. Fig. 10 only shows the DY cross-section ratio of tungsten and deuterium for an illustration. Judged by the data and the dynamical nuclear PDFs, there is a hint that parton energy loss is small but not zero.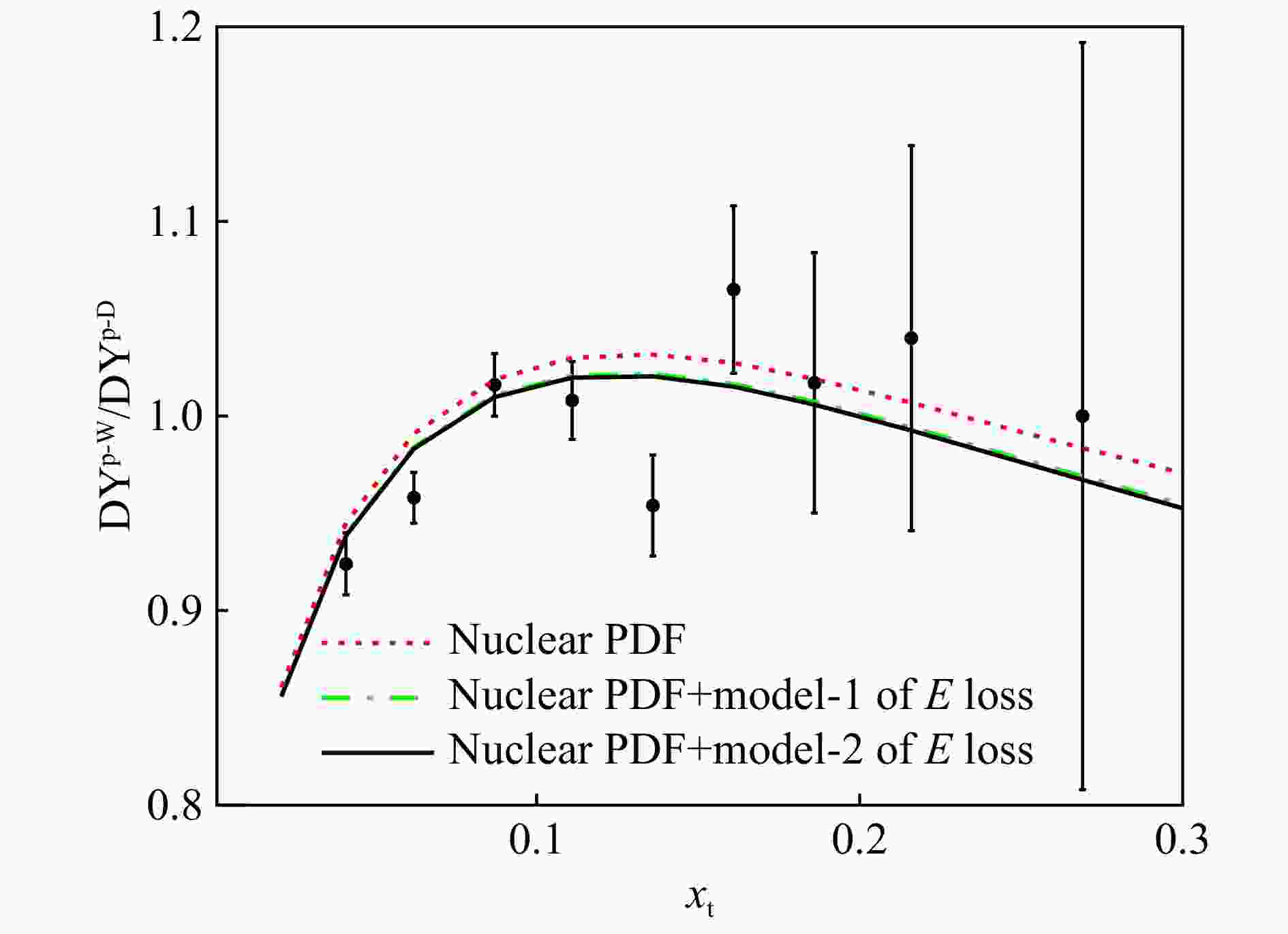
Figure 10. (color online) The Drell-Yan cross-section ratio between Tungsten and Deuterium based on our nuclear dynamical parton distributions as a function of the target parton momentum fraction
$x_t$ , compared with E772 data[36]. -
The dynamical parton distributions of both nucleon and nuclei agree well with the experimental observations. In dynamical parton model, the only input information is the three valence/constitutent quark distributions at an extremely low energy scale (
$ \sim 0.1 $ GeV2). (1) our study shows that PDFs at high$ Q^2 $ can be connected to the quark model picture via the parton-parton recombination corrected DGLAP equations and the saturated running strong coupling$ \alpha_{\rm s }$ . (2) the input valence distributions from MEM is reasonable. (3) nucleon swelling and parton-parotn recombination enhancement explain well the EMC effect and the nuclear shadowing, respectively. (4) it is implied that there is a small parton energy loss in cold nuclear matter from an analysis of E772 and E866 data.
-
摘要: 本工作研究了自由核子和冷原子核物质的动力学产生的海夸克和胶子分布。在动力学部分子模型中,所有的海夸克和胶子纯粹来自DGLAP方程描述的QCD涨落过程,而较少的固有海夸克成分忽略不计。在
$Q_0^2\sim 0.1$ GeV2标度,选择最大熵方法估计的三价夸克分布作为非微扰输入。使用了在低$Q^2$ ($<1$ GeV2)下饱和的跑动强耦合常数。关于原子核效应,考虑了核子变胖和部分子-部分子重组增强的影响。核子及冷核物质的动力学部分子分布均符合实验观测。应用预言的原子核部分子分布抽取得到部分子在穿过冷核物质时的能量损失。Abstract: This paper present a review on the dynamically generated sea quark and gluon distributions in the free nucleon and the cold nuclear medium. In the dynamical parton model, all the sea quarks and gluons come purely from the QCD fluctuations with DGLAP equations, where the small components of intrinsic sea quarks are neglected. The three valence quark distributions from maximum entropy method are taken as the nonperturbative input at$Q_0^2\sim 0.1$ GeV2. The saturated strong coupling at low$Q^2$ ($<1$ GeV2) is used in this work. Nucleon swelling and parton-parton recombination enhancement are considered for the nuclear matter. The dynamical parton distributions of both nucleon and cold nuclear matter are consistent with the experiments. Furthermore, we show a preliminary application of the nuclear parton distributions in the extraction of the parton energy loss penetrating in the cold nuclear medium. -
Figure 4. Comparisons of the predictions from the dynamical parton model with the proton structure function measurements by H1 collaboration[19].
Figure 5.
$Q^2$ -dependence of the predicted proton$F_2$ at large$x$ based on the dynamical parton model, compared with the experiments[20].Figure 8. The predicted nuclear structure function ratios from the nuclear dynamical parton distributions compared with the experimental data[25], for some heavy nuclei, at
$Q^2 = 2~{\rm GeV}^2$ .Figure 10. (color online) The Drell-Yan cross-section ratio between Tungsten and Deuterium based on our nuclear dynamical parton distributions as a function of the target parton momentum fraction
$x_t$ , compared with E772 data[36]. -
[1] ASHMAN J, BADELEK B, BAUM G. Phys Lett B, 1988, 206: 364. doi: 10.1016/0370-2693(88)91523-7 [2] HEN O, MILLER G A, PIASETZKY E, et al. Rev Mod Phys, 2017, 89: 045002. doi: 10.1103/RevModPhys.89.045002 [3] GLUCK M, REYA E, VOGT A. Eur Phys J C, 1998, 5: 461. doi: 10.1007/s100529800978 [4] DULAT S, HOU T J, GAO J. Phys Rev D, 2016, 93: 033006. doi: 10.1103/PhysRevD.93.033006 [5] BALL R D, DEBBIO L D, FORTE S, et al. Nucl Phys B, 2010, 838: 136. doi: 10.1016/j.nuclphysb.2010.05.008 [6] KHALEK R A, ETHIER J J, ROJO J. Eur Phys J C, 2019, 79: 471. doi: 10.1140/epjc/s10052-019-6983-1 [7] HIRAI M, KUMANO S, NAGAI T H. Phys Rev C, 2004, 70: 044905. doi: 10.1103/PhysRevC.70.044905 [8] CHEN Xurong, RUAN Jianhong, WANG Rong, et al. Int J Mod Phys E, 2014, 23: 1450057. doi: 10.1142/S0218301314500578 [9] WANG Rong, CHEN Xurong. Chines Physics C, 2017, 41: 053103. doi: 10.1088/1674-1137/41/5/053103 [10] WANG Rong, CHEN Xurong, FU Qiang. Nucl Phys B, 2017, 920: 1. doi: 10.1016/j.nuclphysb.2017.04.008 [11] DEURA A, BRODSKY S J, DE TERAMONDC G F. Prog Part Nucl Phys, 2016, 90: 1. doi: 10.1016/j.ppnp.2016.04.003 [12] WANG Rong, CHEN Xurong. Phys Rev D, 2015, 91: 054026. doi: 10.1103/PhysRevD.91.054026 [13] ALTARELLI G, PARISI G. Nucl Phys B, 1977, 126: 298. doi: 10.1016/0550-3213(77)90384-4 [14] GRIBOV L V, LEVIN E M, RYSKIN M G. Phys Rep, 1983, 100: 1. doi: 10.1016/0370-1573(83)90022-4 [15] MUELLER A H, QIU J W. Nucl Phys B, 1986, 268: 427. doi: 10.1016/0550-3213(86)90164-1 [16] ZHU Wei, RUAN Jianhong. Nucl Phys B, 1999, 559: 378. doi: 10.1016/S0550-3213(99)00461-7 [17] WANG R, DUPRE R, HUANG Y, et al. Phys Rev C, 2019, 99: 035205. doi: 10.1103/PhysRevC.99.035205 [18] DAI Hongkai, WANG Rong, HUANG Yin, et al. Phys Lett B, 2017, 769: 446. doi: 10.1016/j.physletb.2017.04.015 [19] AARON F D, ALEXA C, ANDREEV V, et al. Eur Phys J C, 2011, 71: 1579. doi: 10.1140/epjc/s10052-011-1579-4 [20] AARON F D, ABRAMOWICZ H, ABT I, et al. Jour High Ener Phys, 2010, 01: 109. doi: 10.1007/JHEP01(2010)109 [21] AMAUDRUZ P, ARNEODO M, ARVIDSON A, et al. Nucl Phys B, 1992, 371: 3. doi: 10.1016/0550-3213(92)90227-3 [22] ARRINGTON J, COESTER F, HOLT R J, et al. J Phys G: Nucl Part Phys, 2009, 36: 025005. doi: 10.1088/0954-3899/36/2/025005 [23] ABRAMOWICZ H, HANSL-KOZANECKI G, MAY J, et al. Z Phys C, 1984, 25: 29. doi: 10.1007/BF01571954 [24] JONES G T, JONES R W L, KENNEDY B W, et al. Z Phys C, 1994, 62: 601. doi: 10.1007/BF01574162 [25] SCHMOOKLER B, DUER M, SCHMIDT A, et al. Nature, 2019, 566: 354. doi: 10.1038/s41586-019-0925-9 [26] SEELY J, DANIEL A, GASKELL D, et al. Phys Rev Lett, 2009, 103: 202301. doi: 10.1103/PhysRevLett.103.202301 [27] GOMEZ J, ARNOLD R G, BOSTED P E, et al. Phys Rev D, 1994, 49: 4348. doi: 10.1103/PhysRevD.49.4348 [28] ADAMS M R, AÏD S, ANTHONY P L, et al. Z Phys C, 1995, 67: 403. doi: 10.1007/BF01624583 [29] ASHMAN J, BADELEK B, BACUM G, et al. Phys Lett B, 1988, 202: 603. doi: 10.1016/0370-2693(88)91872-2 [30] ARNEODO M, ARVIDSON A, AUBERT J J, et al. Nucl Phys B, 1990, 333: 1. doi: 10.1016/0550-3213(90)90221-X [31] AMAUDRUZ P, ARNEODO M, ARVIDSON A, et al. Nucl Phys B, 1995, 441: 3. doi: 10.1016/0550-3213(94)00023-9 [32] BRODSKY S, HOYER P. Phys Lett B, 1993, 298: 165. doi: 10.1016/0370-2693(93)91724-2 [33] BAIER R, DOKSHITZER Y L, MUELLER A H, et al. Nucl Phys B, 1997, 483: 291. doi: 10.1016/S0550-3213(96)00553-6 [34] BAIER R, DOKSHITZER Y L, MUELLER A H, et al. Nucl Phys B, 1997, 484: 265. doi: 10.1016/S0550-3213(96)00581-0 [35] WANG E K, WANG X N. Phys Rev Lett, 2002, 89: 162301. doi: 10.1103/PhysRevLett.89.162301 [36] ALDE D M, BAER H W, GARVEY G T, et al. Phys Rev Lett, 1990, 64: 2479. doi: 10.1103/PhysRevLett.64.2479 [37] VASILIEV M A, REDDO M E, BROWN C N, et al. Phys Rev Lett, 1999, 83: 2304. doi: 10.1103/PhysRevLett.83.2304 -
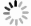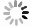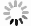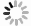











 下载:
下载:




































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号