The cold rearrangement of heavy nuclei at very low or even zero excitation energy proved to be a very extended phenomenon, ranging from $ \alpha $ deacay^[1-2], cluster radioactivity^[3-6] to the cold fission of many actinide nuclei^[7-9]. Experimentally, many works reveal nuclear structure effects in the cold rearrangement processes^[10-11]. It is well known that $ \alpha $ particle is double magic nucleus. In the cold fission shows the occurrence of a few spherical nuclei around the doubly magic nucleus $ ^{132}{\rm{Sn}} $, which is similar to the case of cluster radioactivity, where the daughter nuclei are around $ ^{208}{\rm{Pb}} $. Theoretically, the existence of a valley in the potential energy surface for heavy cluster emission in which one of the emitted fragments is close to the double magic shell has been pointed out^[12-15].

The process of $ \alpha $ decay is fundamentally a quantum-tunneling effect, in which the penetration probability has been calculated using WKB approximation assuming $ \alpha $ particle tunneling through the potential barrier between $ \alpha $ particle and the daughter nucleus^[16-17]. In the unified fission approach the decay constant $ \lambda $ is simply the product of the barrier penetrability $ P $ and of a constant assault frequency $ \nu_{0} $^[18-22]. Then, the height, position and width of the potential barriers are the main ingredients determining the half-lives. In the cluster model, the cluster is assumed to form before it penetrates the barrier and a preformation factor is included in the calculation. The decay constant $ \lambda $ is defined as the product of the preformation factor, the assault frequency and the penetration probability^[23-27]. Usually, computing the $ \alpha $ formation amplitude is a difficult task because the actual wave functions involved cannot be well defined. The $ \alpha $ preformation factor is very important from the viewpoint of the nuclear structure. Numerous studies of the $ \alpha $ decay have been concentrated on this problem.

The spontaneous emission of a charged particle heavier than an $ \alpha $ particle but lighter than a fission fragment was first theoretically predicted at the beginning of 1980s by Sandulescu et al^[3]. In 1984, the emission of $ ^{14}{\rm{C}} $ nucleus by $ ^{223}{\rm{Ra}} $^[4] was observed. Since then, other cluster radioactivities have been observed leading to $ ^{14}{\rm{C}} $, $ ^{20}{\rm{O}} $, $ ^{23}{\rm{F}} $, $ ^{22, 24-26}{\rm{Ne}} $, $ ^{28, 30}{\rm{Mg}} $, and $ ^{32, 34}{\rm{Si}} $ emission, and their partial half-lives have been measured^[28]. The superasymmetric fission model^{[5-6, 29-34]}, which is based on Gamow's idea of barrier penetration; among them the preformed cluster model (PCM)^[35-38], in which the cluster is assumed to be preformed in the parent nucleus and the preformation factor for all possible clusters is calculated by solving the Schrödinger equation for the dynamical flow of mass and charge; in the generalized density-dependent cluster model (GDDCM)^[39] assumed the cluster preformation factor has an exponential form; and a cluster model with a mean-field cluster potential can also provide a good description of cluster emission^[40]. Recently, microscopic calculations of cluster formation probability and of barrier penetrability have been performed^[41-42] by using the R-matrix description of the process. A universal decay law(UDL) for $ \alpha $-decay and cluster radioactivity was recently developed^[42-43] based on this theory.

The cold fission are characterized by large total kinetic energies of the final nuclei approaching the $ Q $ value of the decay. The occurrence of cold fission processes for which no neutron emission takes place and the scission configurations are very compact, leading to a very high total kinetic energy of the final fragments. Cold fission is considered to be identical to spontaneous decay with emission of fragments such as $ ^{14}{\rm{C}} $, $ ^{18, 20}{\rm{O}} $, $ ^{23}{\rm{F}} $, $ ^{22, 24-46}{\rm{Ne}} $, $ ^{28, 30}{\rm{Mg}} $, and $ ^{32, 34}{\rm{Si}} $ emission. The analytical superasymmetric fission model^[44] and the effective liquid drop model^[45] are applied to study cold fission, $ \alpha $ decay and cluster radioactivity in a unified way. In the cluster model, the emitted nucleus and the daughter are supposed to be preborn individually inside the parent nucleus with a definite preformation probability. In many calculations it has been assumed that the preformation factors are taken to be constant^[46-47]. The decay width is well described as a product of three model dependent quantities, namely, the preformation probability of the emitted clusters inside the decaying nucleus, the assault frequency, and the barrier penetration probability^[48-50].

The conventional liquid drop model was developed to include the nuclear proximity energy and a quasi-molecular shapes by G.Royer in 1984, which allows us to describe the fusion, the fission, cluster radioactivity, $ \alpha $ decay and proton emission processes^[51-54]. In the present work we extend GLDM model to include also cold fission processes. The unified treatment of $ \alpha $ decay, cluster radioactivity and cold fission is adopted the GLDM for $ ^{226, 226, 230, 232}{\rm{Th}} $, $ ^{231}{\rm{Pa}} $, $ ^{230, 232, 233, 234, 235, 236}{\rm{U}} $, $ ^{237}{\rm{Np}} $, $ ^{236, 238}{\rm{Pu}} $. The influence of the macroscopic energy coefficient on the spontaneous decay process is considered. It is well know that the macroscopic energy coefficient is a very important character for nuclear structure, as well as for decay process. So it is very interesting to check how much the influence of uncertainty macroscopic energy on the potential barrier as well as the half-life for spontaneous decay process. In addition, we also discuss the uncertainty of inertia coefficients in relation to half-lives.

The total energy of a deformed nucleus is the sum of the GLDM energy and the shell and pairing energies. Within this GLDM the macroscopic energy of a deformed nucleus is defined as^[19]

where the different terms are respectively the volume, surface, Coulomb, nuclear proximity and rotational energies. For one-body shapes, the volume $ E_{{\rm{V}}} $, surface $ E_{{\rm{S}}} $ and Coulomb $ E_{{\rm{C}}} $ energies are given by

The set of parameters $a_{\rm v}=15.494$, $k_{\rm v}=1.8$, $ a_{{\rm{s}}}=17.9439 $ (or 18.18), and $ k_{{\rm{s}}}=1.8 $ (or 3.1) has been used. It is well known that the parameters ($ a_{{\rm{s}}} $ and $ k_{{\rm{s}}} $) in the liquid drop and macroscopic microscopic model were determined from a least-squares fit to the experimental data. There are some differences in the fitting results of different research groups. To study the influence of different parameter on the potential barrier, different parameter values were adopted in our calculations.

The $ B_{{\rm{C}}} $ is the Coulomb shape dependent function, $ S $ is the surface and $ I $ is the relative neutron excess.

where $ V(\theta) $ is the electrostatic potential at the surface and $ V_{0} $ the surface potential of the sphere. The effective sharp radius $ R_{0} $ has been chosen as

This formula proposed is derived from the droplet model and the proximity energy and simulates rather a central radius for which $ R_{0}/A^{1/3} $ increases slightly with the mass. When the fragment are separated^[51],

To ensure volume conservation, $ R_{1} $ and $ R_{2} $ read

where

The discontinuity of a few MeV appearing at the contact point due to the difference between $ A_{1}/Z_{1} $ and $ A_{2}/Z_{2} $ has been linearized from the contact point to the sphere since it originates form discarding the charge rearrangement in the nuclear matter which occurs progressively.

The surface energy comes from the effects of the surface tension forces in a half space. When a neck or a gap appears between separated fragments an additional term called proximity energy must be added to take into account the effects of the nuclear forces between the close surface. It moves the barrier top to an external position and strongly decreases the pure Coulomb barrier:

where

$ r $ is the distance between the mass centres, $ h $ is the transverse distance varying from the neck radius or zero to the height of the neck border, $ D $ is the distance between the opposite surfaces in consideration and $ b $ is the surface width fixed at 0.99 fm. $ \varPhi $ is the proximity function. The surface parameter $ \gamma $ is the geometric mean between the surface parameters of the two fragments.

The shape dependent shell corrections have been determined within the Droplet Model expressions^[55]:

where, the range a has been chosen to be $ 0.32r_{0} $. $\alpha^{2}=(\delta R)^{2}/a^{2}$, the factor $\alpha^{2}$ is the Myers-Swiatecki measure for the deformation of the nucleus. The attenuating factor $({\rm e}^{-\alpha^{2}} )$ makes the whole shell correction energy decrease from maximum to zero with increasing distortion of the nucleus. The distortion is the root-mean-square value of the deviation of the radius vector $ R(\theta.\phi) $, specifying the nuclear surface,

The calculation method of $ E_{{\rm{shell}}}^{{\rm{sphere}}} $ is taken from Ref.[56]. The shape dependent pairing energy has been calculated with the following expressions of the finite-range droplet model^[57].

In the unified fission model, the decay constant of the parent nucleus is simply defined as,

The assault frequency $ \upsilon_{0} $ has been taken as,

In principle, the assault frequency is very complicated, it is intimately linked to nuclear structure information. In the present work, for the sake of simplicity, the assault frequency parameters of fixed values are adopted in our calculations. For all the above results, our calculations for three decay processes were performed with one set of parameters. In fact, the assault frequency of three cluster processes is very different.

The barrier penetrability $ P $ is calculated within the action integral

with $E(R_{{\rm{in}}})=E(R_{{\rm{out}}})=Q_{{\rm{exp}}}$.

The inertia $ B(r) $ has been chosen as^[59]

where

where $ R_{{\rm{cont}}} $ is the sum of $ R_{1} $ and $ R_{2} $.

Accurate knowledge of the $ B(r) $, $ E(r) $ and $ Q $ values is crucial for the calculation, since the WKB penetrabilities are very sensitive to them. The partial half-life is related to the decay constant $ \lambda $ by

The effect of the coefficient of surface asymmetry term ($ k_{{\rm{s}}} $) on $ \alpha $ decay half-lives of heavy nuclei are investigated within GLDM. The numerical results are given in Table 1, in which the second column denotes experimental $ Q $ values. The results calculated by the GLDM are given in the third, fourth, and fifth columns when the coefficients of surface asymmetry are different. The experimental $ \alpha $ decay half-lives are given in the sixth column. As can be seen from the Table 1, the calculated half-lives agree precisely with the experimental data and the ratio between them is approximately within a factor of 4, except for the case of $ \alpha $ decay from odd $ A $ nuclei $ ^{235}{\rm{U}} $, $ ^{231}{\rm{Pa}} $ and $ ^{237}{\rm{Np}} $. In addition, from the Table 1 we can see that the half-life of $ \alpha $ decay is not a sensitive dependency on the coefficient of surface asymmetry term ($ k_{{\rm{s}}} $).

From the decay dynamics studies it is known that spontaneous decay half-lives are very sensitive to the details of the potential barrier. In order to illustrate the influence of $ k_{{\rm{s}}} $ on the barriers, the potential barrier governing the $ ^{28}{\rm{Mg}} $ emission from $ ^{234}{\rm{U}} $ is displayed in Fig.1(b). The potential barrier is constructed by a GLDM, taking into account the nuclear proximity, the mass asymmetry, the accurate nuclear radius, the phenomenological shell and pairing correction. The dashed and solid curve show the potential barrier with the different $ k_{{\rm{s}}} $ value. From Fig.1 that the potential barrier changes when $ k_{{\rm{s}}} $ changed from 1.8 to 3.1. This will directly affect the half-lives of cluster radioactivity. One can see clearly from Fig.1 that the influence of the coefficient of surface asymmetry is strongly dependent on the charge asymmetry $\eta^{}_{Z} = (Z_{1}-Z_{2})/(Z_{1}+Z_{2})$ for the same parent nucleus during the rearrangement process. With the decrease of the chagre asymmetry $\eta^{}_{Z}$, the influence of the change of the macroscopic energy coefficient on the potential is more obvious.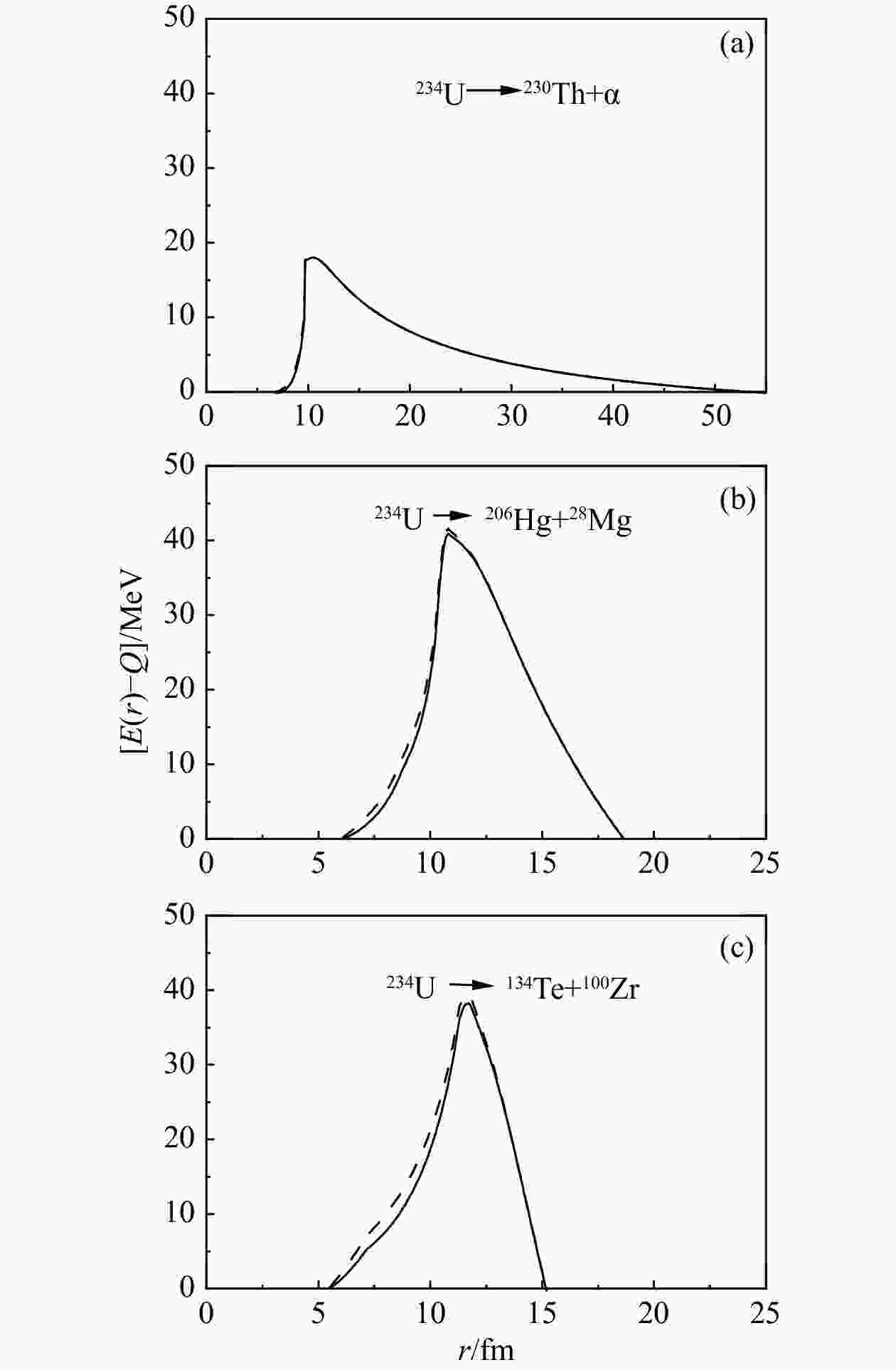

Figure 1.  The change of the potential barrier caused by the asymmetry of surface $ k_{{\rm{s}}} $ from 1.8 to 3.1, $ k_{{\rm{s}}} $ values are 1.8 (solid line) and 3.1(dashed line) descriptions for $ \alpha $ decay (a), cluster radioactivity (b), and spontaneous cold fission process (c) of the $ ^{234}{\rm{U}} $ parent nucleus. $ r $ is the distances between the mass centers.

We have systematically calculated the cluster radioactivity half-lives from $ ^{226}{\rm{Th}} $ to $ ^{242}{\rm{Cm}} $ by using GLDM taking into account the influence of $ k_{{\rm{s}}} $ and inertia coefficient on half-lives. The detailed results are listed in Table 2, in which the first column denotes the parent nuclei and the second column denotes $ Q $ values. The results calculated by the GLDM considering the coefficient of surface asymmetry $ k_{{\rm{s}}} $ of different are listed in the third and fourth columns. One can see that the cluster emission half-lives is increased along with the increasing of $ k_{{\rm{s}}} $ from 1.8 to 3.1, while the other parameters is fixed. In this sense, the calculated cluster radioactivity half-lives depend on the coefficient of surface asymmetry $ k_{{\rm{s}}} $. In order to consider the influence of inertia coefficient on half-lives, in the sixth column of Table 2 are shown the corresponding results of half-lives of the cluster radioactivity in which were calculated by different values of inertia coefficient. Because surface energy depends on deformation, the change of surface energy coefficient also has influence on potential barrier. If we choose the surface energy coefficient as the latest fitting result $a_{\rm s}=18.18$^[60], we can find that the change of the surface energy coefficient makes the half-lives of the radioactivity of the cluster have certain influence by comparing the results of fifth and sixth columns. It can be found from the third to the sixth columns in Table 2 that the deviations between the experimental data and the calculated values are less than $ 10^{2} $ for the most nuclei. Through the analysis, it is found that, although the surface energy coefficient ($ a_{\rm s} $), the surface asymmetry coefficient ($ k_{{\rm{s}}} $) and the inertia coefficient ($ B(r) $) have influence on the half lives of the cluster radioactivity, but the change of these values will not make the uncertainty of half-lives more than two order of magnitude.

It is well known that the symmetry energy coefficient of finite nuclei is usually extracted by directly fitting the measured nuclear masses with different versions of the liquid drop mass formula. Some different forms for describing the mass dependence of symmetry energy coefficients of finite nuclei, which divide the symmetry energy of a nucleus into the volume and surface contributions, were proposed in Refs. [60-61]. The mass dependence of symmetry energy of the nucleus has been adopted in the GLDM model,

The symmetry energy coefficient $ a_{{\rm{sym}}} $ is expressed,

where $ c_{{\rm{sym}}}=a_{{\rm{v}}}k_{{\rm{v}}}=27.889 $, $\kappa=(a_{{\rm{s}}}k_{{\rm{s}}} )/(a_{\rm v}k_{{\rm{v}}})=0.643~k_{{\rm{s}}}$. Because of the volume conservation, the contribution of the symmetry energy coefficient from the volume energy ($ c_{{\rm{sym}}} $) is always zero when the shape evolution from one body to two separated fragments is adopted unified way. Therefore, the contribution of the surface part of the symmetry energy coefficient is crucial for the reasonable description of the potential barrier and half-lives. In the framework of the GLDM model, if the coefficient of surface asymmetry $ k_{{\rm{s}}} $ is 1.8, the symmetry energy coefficient is about 22.89. This value is very close to the latest results of the symmetric energy coefficient of finite heavy nuclei^[60-61]. Although the difference of the symmetry energy coefficients of finite nuclei given by different theoretical work is very small, the proportion of surface terms (the symmetry energy coefficient of a nucleus into the volume and surface contributions) in the symmetry energy coefficient is not completely determined. For example, in the work of Danielewicz et al.^[60], the contribution of the surface term to the symmetry energy coefficient is approximately 17% for the present study region. However, in the work of Wang et al.^[61], the contribution of the surface in the symmetry energy coefficient is approximately 25%. In the present work, the contribution of the surface terms to the symmetry energy coefficient is changed from 18% to 26% when the surface asymmetry coefficient $ k_{{\rm{s}}} $ is changed from 1.8 to 3.1. It can be seen from the present results that the difference of surface terms has an certain influence on the cluster radioactivity process.

In order to unify the view of $ \alpha $ decay, cluster radioactivity and cold fission, it is quite natural to interpret cold fission as a cold rearrangement process with fragments in their ground states, in an analogous way with the cluster radioactivity. Thus the cold fission process reduces to the penetration of a potential barrier. The numerical results are given in Table 3, one can see that in the cold fission process correspond to one of the fragments close to the double magic nucleus $ ^{132}{\rm{Sn}} $, in which the second column denotes $ Q $ values. The results calculated by the GLDM considering different surface asymmetry coefficient $ k_{{\rm{s}}} $ are listed in the third and fourth columns. The experimental cold fission half-lives are given in the last column^[62]. From the fission dynamics studies it is known that fission half-lives are very sensitive to the details of the potential barrier and the inertia coefficient^[59]. From the Table 3 of the results show that the uncertainty of surface asymmetry and inertia coefficients have a significant effect on the theoretical calculation of the cold fission half-lives. The GLDM model is to reach a reasonable calculation for the half-lives for cold fission processes. By demonstrating the detailed results, we would like to point out the sensitivity of the calculated cold fission half-lives to the macroscopic energy coefficient and the inertia coefficient.

The $ \alpha $ decay, cluster radioactivity and cold fission can be unified description in as a spontaneous tunneling process via quasi-molecular shapes. The potential barrier has been studied within a generalized liquid-drop model taking into account the phenomenological shell and pairing correction. The spontaneous nuclear decay ($ \alpha $ decay, cluster radioactivity and cold fission) half-lives have been calculated within the WKB barrier penetration probability. The present model is to continue reproducing the experimental data for $ \alpha $ decay and cluster radioactivity, as well as to reach a reasonable calculation for the half-lives for cold fission processes. From calculations, it is found that the influence of uncertainty of macroscopic energy coefficient on the potential barrier and half-lives are strongly dependent on the charge asymmetry [$\eta^{}_{Z} = (Z_{1}-Z_{2})/(Z_{1}+Z_{2})$] for the same parent nucleus during the rearrangement process. The influence of uncertainty of inertia coefficient on half-lives obviously depend on the mass asymmetry $\eta^{}_{Z}$.

Acknowledgments The work is supported by the National Natural Science Foundation of China(Grants No.12175064, U2167203). Hunan Outstanding Youth Science Foundation (2022JJ10031) and Hunan Provincial Education Department(Key project 20A290).