Local Correlation and Log-scale N_pN_n Scheme of ${{2_1^+ }}$ Quadrupole Moments in Even-even Nuclei

原子核在一个主壳层内的核结构演化主要是由质子和中子相互作用(pn相互作用)驱动的^[1-3]。如果每对质子和中子的耦合具有类似的相互作用，那么原子核中剩余质子中子相互作用应大致与$ N_{\rm{p}}N_{\rm{n}} $乘积成正比。这里的$ N_{\rm{p}} $、$ N_{\rm{n}} $分别对应价质子数与价中子数。另一方面，偶偶核的第一个$ 2^+ $态能量及其跃迁至基态的约化跃迁几率也体现出原子核的结构演化特征，因而应该在$ N_{\rm{p}}N_{\rm{n}} $乘积参数的组织下呈现出区域系统性规律^[4]。为简化描述，后文中$ E_{2^+_1} $代表偶偶核的第一个$ 2^+ $态能量；$B({\rm{E2}})$代表偶偶核的第一个$ 2^+ $态向下跃迁的约化跃迁几率。受此启发，Casten^[5-7]提出了$ N_{\rm{p}}N_{\rm{n}} $ scheme，将这些可观测值与重核的$ N_{\rm{p}}N_{\rm{n}} $乘积相对应，观察其平滑演化规律。这种研究方法也进一步地被广泛应用于核结构数据的整理，发掘其中的异常演化因素及其所对应的微观机制^[8-12]。

虽然$ N_{\rm{p}}N_{\rm{n}} $系统性规律研究取得了一些成功，但是价核子数与质子中子剩余相互作用之间的具体关联并未量化，而质子中子剩余相互作用与各类原子核可观测量之间的关系也只有定性描述，因而很难定量、解析地将$ N_{\rm{p}}N_{\rm{n}} $乘积与核可观测量相联系。为了解决这一困难，前人尝试通过预设解析公式来拟合$ N_{\rm{p}}N_{\rm{n}} $系统性规律，从而为实验预估服务。早在$ N_{\rm{p}}N_{\rm{n}} $系统性规律被提出之前，前人已注意到B(E2)与$ N_{\rm{p}}N_{\rm{n}} $之间大致成正比关系^[4]，并进一步提出$ Q $也有可能满足这一正比关系。此后，很多工作尝试将原子核可观测量与$ N_{\rm{p}}N_{\rm{n}} $乘积的指数函数相联系^[11-12]，取得了一些定量认识。

最近我们注意到一些与原子核四极形变相关的可观测量，如$ E_{2^+_1} $、B(E2)、电荷半径等，除了服从$ N_{\rm{p}}N_{\rm{n}} $系统性规律以外，本身也满足一些局域系统性关联^[13-15]。这些局域关联一般表现为相邻原子核物理量通过一些简单的代数关系联系在一起。这些局域关联已被用于预言未知核数据，如$ E_{2^+_1} $与B(E2)^{[14, 16]}、原子核质量^[17-21]、单核子分离能^[22]、核电荷半径^[23]等等。与$ N_{\rm{p}}N_{\rm{n}} $系统性规律相比，局域关联的核结构理论基础可能更为明确，这主要是因为核结构模型的局域化。如果两个原子核在核素图上彼此相距很远，那么它们的理论模型参数应该非常不同，甚至在模型框架方面也有明显差异，因而无法通过统一的核模型直接给出一个大壳内的$ N_{\rm{p}}N_{\rm{n}} $系统性规律。然而相邻核的模型描述是趋同的，那么就可能从这样的模型中提取原子核可观测量的局域系统性关系，如$ E_{2^+_1} $和B(E2)的局域关系就是由Hartree-Fock模型推导得到的^[24]。

近来，通过将原子核$ E_{2^+_1} $、B(E2)局域关系微分化，我们得到了它们的$ N_{\rm{p}}N_{\rm{n}} $系统性规律的解析表达^[25]。这相当于在$ N_{\rm{p}}N_{\rm{n}} $系统性规律与原子核模型之间建立了一定的联系。电四极矩$ Q $与$ E_{2^+_1} $、$B({\rm{E2}})$类似，都是核四极形变的重要表征，应该可以使用$ N_{\rm{p}}N_{\rm{n}} $乘积来进行系统性描述^[4]。如果电四极矩也存在着类似于$ E_{2^+_1} $、$B({\rm{E2}})$的局域系统性关系，那么就可以进一步给出电四极矩$ N_{\rm{p}}N_{\rm{n}} $系统性规律的解析表达。此前与$ E_{2^+_1} $、B(E2)相比，电四极矩的实验数据相对比较匮乏，针对电四极矩的$ N_{\rm{p}}N_{\rm{n}} $系统性演化规律与局域关联的讨论相对比较稀少。随着电四极矩实验数据的日益充溢，应该尝试开展这方面工作。因此，本文将首先通过理论模型构建电四极矩的局域关联，并使用实验数据验证这些局域关联。其次，沿用文献 [25]中的逻辑，本文将进一步使用实验数据来验证电四极矩是否也存在这种对数$ N_{\rm{p}}N_{\rm{n}} $线性关系，分析其中的例外数据异常因素，为电四极矩实验数据分析与预估提供新手段。

本节将从理论模型出发推导$ Q $值可能存在的局部关系。针对不同类型的原子核，使用不同的核结构唯象模型。

具有轴对称形变的转动核适用于轴对称转子模型^[26]，其$ Q $值与内禀四极矩成正比。如假定形变单粒子基下的组态混合对于内禀电四极矩的贡献可以忽略，那么有

其中$ K=0 $, $ I=2 $对应于基带中的$ 2^+_1 $态；$ |\phi_0\rangle $是由变形单粒子态$ |i\rangle $构造的Hartree-Fock基态；$ \hat{T}({\rm E2}) $为电四极算子。假设相邻原子核具有相似的变形质子单粒子态，

振动原子核具有非零$ Q $值源自于声子态的组态混合^[27]，其对应的唯象模型为非简谐振子模型^[27]。为简化推导，模型空间只包含一声子态和两声子态，分别用$ |1\rangle=b^\dagger|0\rangle $和$ |2\rangle=\frac{1}{\sqrt{2}}(b^\dagger)^2|0\rangle $表示。其中$ b^\dagger $为声子产生算符；$ |0\rangle $为声子真空态。相应的哈密顿算符为

其中$ \hbar\omega $是声子激发能；$ \lambda $是声子组态混合能。相应的哈密顿矩阵为

$ 2_1^+ $态对应于$ |1\rangle $和$ |2\rangle $的低激发组态混合

其中$ \alpha $和$ \beta $为实数，对应于两种声子态在$ 2^+_1 $态中所占比重。典型振动原子核的声子态混合并不剧烈，也就是说$ \lambda\lll\hbar\omega $，使得$ \beta\approx\lambda/\hbar\omega $，而 $ \alpha\approx1 $。因此，$ 2^+_1 $态可写作$ |2_1^+\rangle\sim |1\rangle+\frac{\lambda}{\hbar\omega}|2\rangle $。在振子模型中，原子核的电四极算符可唯象写作

$ \chi $是$ \hat{T}({\rm E2}) $算符的强度参数。那么$ 2_1^+ $态的$ Q $值可通过以下公式计算

声子激发能$ \hbar\omega $可以看作是$ Z $和$ N $的平滑函数。在相邻原子核中，它应该近似保持不变。组态混合能参数$ \lambda $与$ pn $相互作用相关^[1]。因此，振动核的$ Q $值应是$ N_{\rm{p}}N_{\rm{n}} $乘积的平滑函数。这符合电四极矩的$ N_{\rm{p}}N_{\rm{n}} $系统性规律设想^[4]。振动原子核一般形变不大，价核子较少，$ N_{\rm{p}}N_{\rm{n}} $也比较小。因此，$ Q $可以围绕$ N_{\rm{p}}N_{\rm{n}}=0 $进行泰勒展开，如下

那么$ Q $值就有局域二阶差分如

注意此处$\frac{{\rm d}Q}{{\rm d}(N_{\rm{p}}N_{\rm{n}})}$未定，还并没有得到严格类似于式(2)的局域关联。但是考虑到，当$ N_{\rm{p}}N_{\rm{n}}=0 $时，核系统中没有pn剩余相互作用，即$ \lambda=0 $，对应于无声子态混合。根据式(7)，$ Q|_{N_{\rm{p}}N_{\rm{n}}=0}\equiv0 $。四个相邻原子核的平均$ Q $值应为$\bar{Q}=(N_{\rm{p}}+1)(N_{\rm{n}}+1)\frac{{\rm d}Q}{{\rm d}(N_{\rm{p}}N_{\rm{n}})}$。对于非幻数振动核，$N_{\rm{p}}\geqslant 2$，$N_{\rm{n}}\geqslant 2$。因此有$ \bar{Q}\gg\delta Q $。换句话说，即使在振动原子核中，局域二阶差分$ \delta Q $相对于原子核电四极矩本身的数值大小仍是很小的。再考虑到实验数据的不确定性，可以认为

因此不论是转动核还是振动核，根据本文推导，原子核的电四极矩都应满足式(10)。

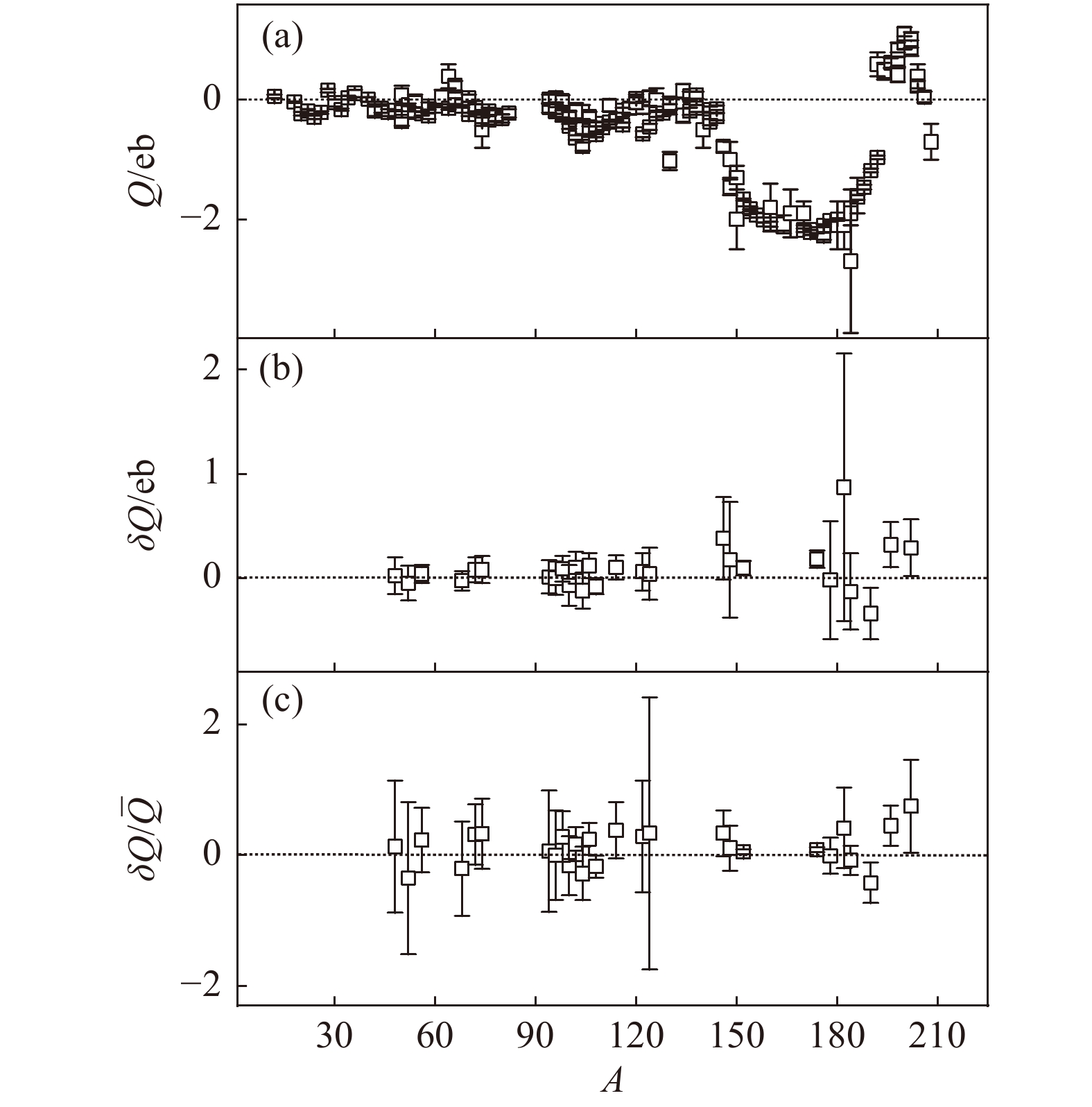
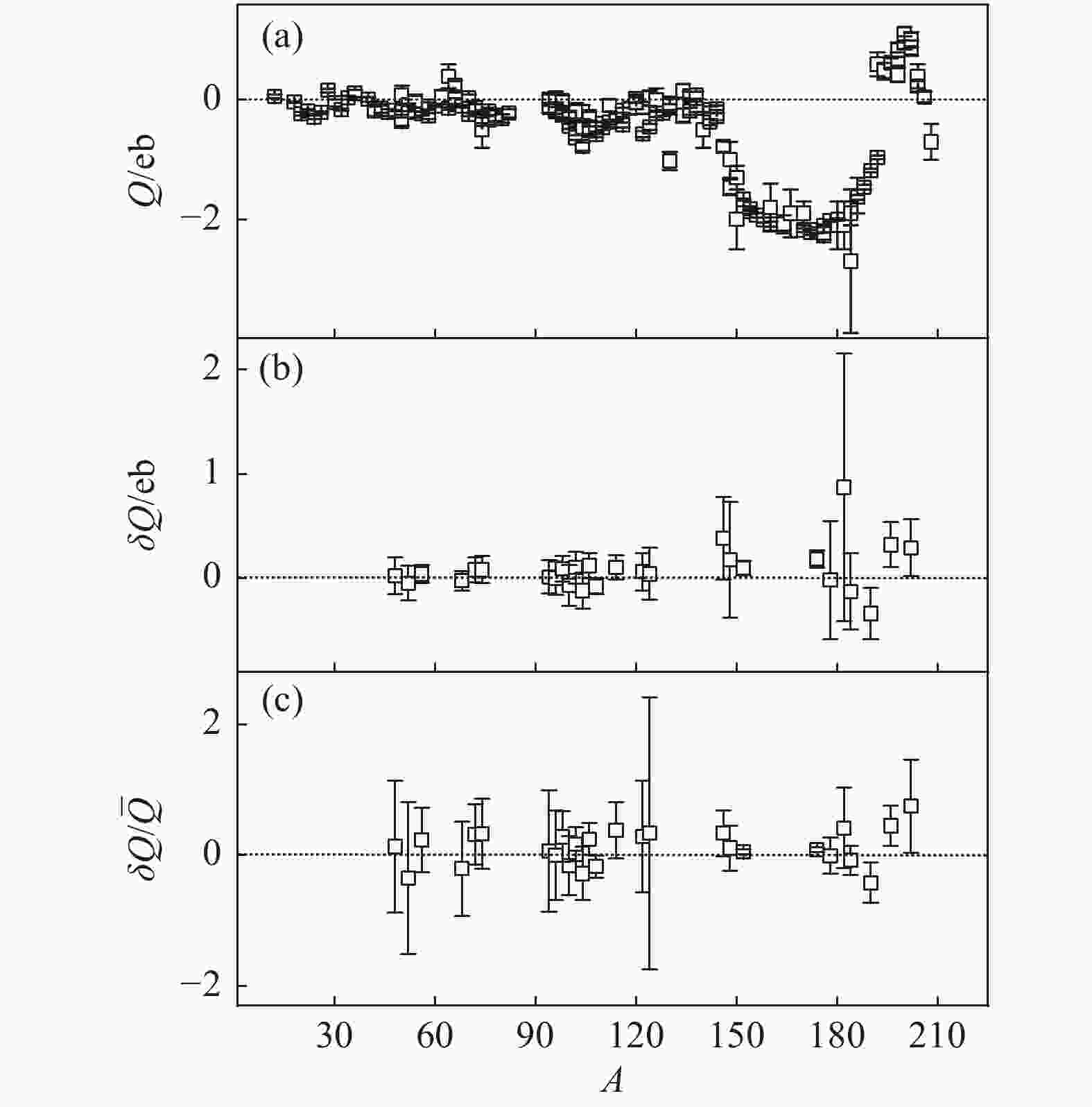
使用电四极矩实验数据^[28-29]可以验证式(10)的可靠性。图1(a)给出了所有实验可用的$ Q $值。图1(b)给出了通过式(10)计算的$ \delta Q $值。可见所有核区中的$ \delta Q $值都在实验误差范围内接近于零。因此，我们可以根据式(10)及现有实验数据^[28]对相邻原子核的未知电四极矩$ Q $进行了预言。表1给出了这些预言值，可为后续实验提供参考。

另一方面，如图1(a)所示，在$ A<130 $核区时，电四极矩数值大多接近$ Q=0 $。这就意味着式(10)在小质量核区成立有可能只是因为较小的电四极矩，而并非相邻原子核局域关联的具体体现，因而有可能是平庸的。为了分辨式(10)在小质量核区是否平庸，我们在图1(c)中进一步给出了$ \frac{\delta Q}{\overline Q} $比例($ \overline Q $为四个相邻原子核电四极矩的平均值)，以体现$ \delta Q $的相对大小。可见$ \frac{\delta Q}{\overline Q} $在误差范围内仍普遍接近于0，说明电四极矩的局域关系在小质量核区也并不平庸。它在轻核区与重核区具有相同的可靠性。我们也注意到$ E_{2^+_1} $与B(E2)也具有类似的相对比例稳定性^[24]，说明这种局域关联可能是原子核四极集体性质的普遍特征。

与$ E_{2^+_1} $、B(E2)类似，如果$ Q $既具有$ N_{\rm{p}}N_{\rm{n}} $系统性演化规律，又满足式(10)中的局域系统性关联，那么$ Q $就应该在对数$ N_{\rm{p}}N_{\rm{n}} $坐标下进行线性演化。为推得这样的线性关系，首先将$ Q $的局域关系微分化有

由于电四极矩$ Q $是$ N_{\rm{p}}N_{\rm{n}} $乘积的函数，那么上述偏导方程可转化为以$ N_{\rm{p}}N_{\rm{n}} $为自变量的二阶常微分方程

上述常微分方程的通解为

其中$ c_1 $、$ c_2 $为任意常数。这就是电四极矩在$ N_{\rm{p}}N_{\rm{n}} $对数坐标下的线性演化规律。

为了验证这样的线性关联，需要在不同核区中绘制电四极矩实验数据随$ \ln(N_{\rm{p}}N_{\rm{n}}) $的演化。在轻核区，由于原子核壳层较小，$ N_{\rm{p}}N_{\rm{n}} $数值变化范围不大，原子核各类可观测量的$ N_{\rm{p}}N_{\rm{n}} $系统性规律并不明显。具体到原子核电四极矩，虽然其具有普适的局域关系，但是它在$ N_{\rm{p}}N_{\rm{n}} $对数坐标下的线性关联并不明显。因此，本节仅在三个重核区($ A\simeq130 $、$ A\simeq150 $和$ A\simeq190 $)分析电四极矩实验数据^[28-29]的对数$ N_{\rm{p}}N_{\rm{n}} $线性行为。这三个重核区是由50、82和126三个幻数分隔而成，具体核子数范围如表2所列。

图2分别展示了电四极矩在上述核区随$ \ln(N_{\rm{p}}N_{\rm{n}}) $的演化规律。作为对比，$ E_{2^+_1} $与B(E2)随$ N_{\rm{p}}N_{\rm{n}} $对数的演化也一并呈现。可以看到，图2所描述的三个核区$ Q $值(特别是$ A\simeq150 $核区)不仅具有$ N_{\rm{p}}N_{\rm{n}} $系统性规律，还表现出明显的对数$ N_{\rm{p}}N_{\rm{n}} $线性关联。而其它两个核区的部分数据对线性的偏离也都有具体的原因，详述如下。

在$A \simeq 130$的核区，如图2(a)所示，部分Ba同位素$ Q $实验测量值看似并不满足$ N_{\rm{p}}N_{\rm{n}} $对数线性关联。这种偏离主要源自于实验测量的不确定性。由于$A \simeq 130$核区原子核位于近球形核到形变核的过渡区域^[31-32]，同一实验测量可以给出了多个不同的电四极矩数值^[33-34]。一部分测量值满足对数$ N_{\rm{p}}N_{\rm{n}} $线性关系，而另一部分则有所偏离。此前实验无法先验地排除这种数据分歧。但我们在表3中细致列出了这些有分歧的实验测量结果，并将它们划分为“满足线性”及“不满足线性”两部分，分别对应在图2(a)满足线性的实验数据及不满足对数$ N_{\rm{p}}N_{\rm{n}} $线性的实验数据。在图2(a)中进一步将“不满足线性”的数据点用蓝色圆点进行标记。在排除这些“不满足线性”的$ Q $值后，实验数据的规律性更为明显。我们相信“满足线性”的$ Q $实验测量更符合$ N_{\rm{p}}N_{\rm{n}} $系统性规律，也更为可靠。因此，$ Q $的对数$ N_{\rm{p}}N_{\rm{n}} $线性规律在一定程度上可以为电四极矩测量结果可靠性评估提供了新的判别标准。

在$A \simeq 190$核区，除了少数Pt同位素($Z = 78$)和$ ^{204} {\rm{Hg}}$之外，整体实验数据呈线性趋势。这些Pt及$ ^{204} {\rm{Hg}}$的电四极矩数据点也在图2(c)中用蓝色圆点突出显示。Pt同位素在$A \sim 190$附近$ N_{\rm{p}}N_{\rm{n}} $系统性规律中的异常表现实际上已被注意到^[33]，并被归因于它们的核形状复杂性^[36]。这些Pt同位素的形变包括软$ \gamma $三轴形变、扁椭以及长椭。不同形变的内禀电四极矩有较大差别，导致在局部偏离$ N_{\rm{p}}N_{\rm{n}} $系统性规律。

另一方面，$ ^{204} {\rm{Hg}}$的$ Q $值非常小，不符合线性。这是因为$ ^{204} {\rm{Hg}}$已非常接近幻数，它的$ Q $值本身应该是一个小量。对于振动核，当$ N_{\rm{p}}N_{\rm{n}} $乘积趋近于零时，$ Q $值也应趋于零。因此，我们在图2(c)中画出一条连接主线性终点和($N_{\rm{p}}N_{\rm{n}} \simeq 0$, $Q = 0$)点的虚线，示意性地体现出$ Q $值在$ N_{\rm{p}}N_{\rm{n}}\rightarrow0 $处的演化趋势。$ ^{204} {\rm{Hg}}$数据点正好位于这条虚线上。因此，我们认为$A \sim 190$核区的电四极矩演化可能对应于分段的线性函数，与B(E2)、$ E_{2^+_1} $的线性演化类似^[25]。由于$A \sim 190$核区在$ N_{\rm{p}}N_{\rm{n}}\rightarrow0 $处的$ Q $实验数据还不够丰富，这种$ N_{\rm{p}}N_{\rm{n}}\rightarrow0 $处的分段线性演化趋势仍有待实验验证。

原子核四极形变$ N_{\rm{p}}N_{\rm{n}} $演化在$ N_{\rm{p}}N_{\rm{n}} $很大时应具有饱合性^[9]。如图2(e)~(f)所示，$ E_{2^+_1} $在$A \sim 150, \,190$核区，当$N_{\rm{p}}N_{\rm{n}} > 100$时，其演化驱于平缓；而图2(g)~(i)则说明B(E2)在$N_{\rm{p}}N_{\rm{n}} \sim 80$处有线性斜率突变的情况。这两种现象都应是$ N_{\rm{p}}N_{\rm{n}} $演化饱合性的具体体现。与$ E_{2^+_1} $以及B(E2)相比，电四极矩线性演化的饱合性并不显著。在$A \sim 130$区，$ N_{\rm{p}}N_{\rm{n}} $较时的数据比较稀少，无法对其演化的饱合性作出判断；在$A \sim 150, \, 190$区，可以隐约看到其演化在$N_{\rm{p}}N_{\rm{n}} > 120$开始有所变化，但这一转变远未完成。总的来说，电矩的$ N_{\rm{p}}N_{\rm{n}} $演化的饱合性研究需要更多的实验数据支持。

综上所述，我们根据轴对称转子模型和非简谐振子模型获得了$ Q $局域系统性关联。如果$ Q $也满足$ N_{\rm{p}}N_{\rm{n}} $系统性规律，那么$ Q $应该在对数坐标的$ N_{\rm{p}}N_{\rm{n}} $ scheme中呈现出线性关联特征。我们用实验数据验证了$ Q $值的局域关联以及其在$ N_{\rm{p}}N_{\rm{n}} $对数坐标下的线性演化。除少数可解释例外，局域关联和对数$ N_{\rm{p}}N_{\rm{n}} $线性规律普遍成立。

我们使用$ Q $的局域关系，基于现有实验数据，对一些未知电四极矩进行预言，可以为未来实验提供参考。$ Q $在$ N_{\rm{p}}N_{\rm{n}} $对数坐标下的线性规律在某种程度上解决了Ba同位素$ Q $值实验测量的不确定性问题。我们也指出在$A \sim 190$核区，由于实验数据的缺乏，$ N_{\rm{p}}N_{\rm{n}}\rightarrow0 $处的分段线性规律，以及$N_{\rm{p}}N_{\rm{n}} \sim $120时的饱合性转变还未突显。这对该核区的电四极矩实验测量提出了新的需求与预期。总之，电四极矩的局域系统性关联及其在对数$ N_{\rm{p}}N_{\rm{n}} $坐标下的线性规律为核结构演化研究提供了更清晰的视野，可能有助于电四极矩实验数据的验证与预言。