-
合成新核素、扩展核素图是核物理研究的基本任务之一。在过去100余年的时间里,新核素的发现和合成工作取得了长足的进步[1]。尤其是在近二十年里,由于加速器和探测技术的发展,新核素的发现数量呈现出新一轮井喷式的增长。例如,在2010年发现的新核素超过了100种[2]。截止到2020年底,已经有3312种核素被发现[3]。然而一些理论预言指出,尚未发现的核素超过了7 000种[4-5]。这些未知的核素主要是远离
$ \beta $ 稳定线的极端丰中子核和超重丰中子核[6]。合成这些极端丰中子核素有以下重要的意义:(1)扩展原子核物理的研究对象;(2)研究它们的奇异结构和奇异衰变性质;(3)检验和发展现有的核结构理论模型;(4)确定核天体物理中的r - 过程路径等等。目前,实验上合成丰中子新核素主要采用多重碎裂方法[7-9]。一般采用中高能的
$ ^{238} {\rm{U}}$ 束轰击铍、铅等稳定靶,结合先进的分离和鉴别技术,极大提升了丰中子新核素的鉴别效率,一次实验通常能鉴别出几十个新核素。例如,2012年Kurcewicz等[7]在德国Darmstadt重离子研究所(GSI)采用1 GeV/nucleon的$ ^{238} {\rm{U}}$ 轰击铍靶,该实验鉴别出60个丰中子新核素。2018年Fukuda等[8]和Shimizu等[9]在日本理化研究所(RIKEN)用345 MeV/nucleon的$ ^{238} {\rm{U}}$ 轰击铍靶,分别鉴别出29个和36个丰中子新核素。实验结果显示这些丰中子新核素由两种反应机制产生:一种是飞行中裂变(in-flight fission),另一种是冷碎裂(clod-fragmentation)。由飞行中裂变机制产生的丰中子新核素其质量数一般小于180,相应的产生截面约为1$ \sim 100$ nb量级。由冷碎裂机制产生的丰中子新核素的质量数一般介于180和238之间,但产生截面非常低,如$ ^{208} {\rm{Pt}}$ 的截面仅为0.002 7 nb[7],这已经接近目前探测器的极限,继续采用多重碎裂方法合成新的丰中子核,尤其是合成较重的丰中子新核素将变得异常困难。另外,多重碎裂方法的致命缺点是它不能产生$ Z>92 $ 的丰中子新核素。多核子转移反应被认为是产生丰中子新核素的有效方法,也是产生超重丰中子核的唯一方法。近年来,多核子转移反应受到了理论家和实验家的广泛关注[10-37]。2008年,Zagrebaev等[10]利用朗之万方程研究了
$ ^{136} {\rm{Xe}}$ +$ ^{208} {\rm{Pb}}$ 的多核子转移反应,其研究结果显示:产生截面大于1$ \mu {\rm{b}}$ 的丰中子新核素约有50种。2015年,Watanabe等[31]在法国GANIL实验室开展了$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 的多核子转移反应实验,其入射能量为7.98 MeV/nucleon,反应产物的鉴别采用直接粒子鉴别技术——VAMOS++[38]。该实验发现了两个重要的现象:(1)和多重碎裂方法相比,多核子转移反应方法在产生$ N = 126 $ 丰中子核素的截面上具有显著的优势;(2)丰中子同位素产生于反应中具有较小能量损失的事件。但该实验并没有发现新的丰中子核素,主要是因为目前VAMOS++系统的探测极限约为0.1 mb量级。2019年,Desai等[36-37]在美国Argonne国家实验室也开展了$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 的多核子转移反应实验,但入射能量为5.59 MeV/nucleon,反应产物通过分析特征$ \gamma $ 射线来鉴别。由于丰中子新核素的特征$ \gamma $ 谱线是未知的,因此该实验缺乏丰中子新核素的鉴别能力。确定多核子转移反应中丰中子核的产生机制是当前亟待解决的问题,它对实验上合成中子新核素具有非常重要的意义。在多核子转移反应中,核子的转移过程受多个因素的共同影响,如体系同位旋、形变、激发能、集体振动等,且各因素之间具有强的关联性。因此,多核子转移反应极其复杂。根据反应产物的总动能-质量(TKE-Mass)分布,可将多核子转移反应划分为三种类型的碰撞:准弹性碰撞、深度非弹性碰撞和准裂变反应[39-41]。考虑到这三种碰撞机制的反应时间尺度不同,本文将在ImQMD模型框架下研究
$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 体系的多核子转移反应,通过弹靶接触时间来划分不同的反应机制,再根据不同弹靶接触时间下反应产物的双微分截面分布和同位素截面分布确定丰中子核的产生机制。 -
在ImQMD模型中[42-45],每个核子由相干态的高斯波包描述,波包中心的演化遵循正则方程:
$$ \dot{{\boldsymbol{r}}}_{i} = \frac{\partial H}{\partial {\boldsymbol{p}}_{i}},~~~ \dot{ {\boldsymbol{p}}}_{i} = -\frac{\partial H}{\partial {\boldsymbol{r}}_{i}}{\text{。}} $$ (1) 体系的哈密顿量由势能和动能
$ T = \sum\limits_{i} \frac{{\boldsymbol{p}}_{i}^{2}}{2m} $ 两部分组成:$$ H = T+U_{\rm{Coul}}+U_{\rm{loc}}{\text{。}} $$ (2) 其中,库仑能
$ U_{\rm{Coul}} $ 为直接项和交换项之和:$$\begin{split} U_{\rm{Coul}} =& \frac{1}{2}\mathop{{\displaystyle\iint}}{\rho_{\rm p}({\boldsymbol{r}})} \frac{e^{2}}{|{\boldsymbol{r}}-{\boldsymbol{r}}'|}{\rho_{\rm p}({\boldsymbol{r}}')}{\rm d}{\boldsymbol{r}}{\rm d}{\boldsymbol{r}}'- \\& e^{2}\frac{3}{4}\Big(\frac{3}{\pi}\Big)^{1/3}\int \rho_{\rm p}^{4/3}{\rm d}{\boldsymbol{r}}, \end{split}$$ (3) $ \rho_{\rm p} $ 是质子的密度。核相互作用势能由Skyrme能量密度泛函给出:$$ U_{{{\rm loc}}} = \int V_{ {\rm loc}}({\boldsymbol{r}}){\rm d}{\boldsymbol{r}}{\text{。}} $$ (4) 核相互作用势可以表示为
$$ \begin{split} V_{{\rm{loc}}} = &\frac{\alpha}{2}\frac{\rho ^{2}}{\rho _{0}}+\frac{\beta }{\gamma +1} \frac{\rho ^{\gamma +1}}{\rho _{0}^{\gamma }}+\frac{{g}_{\rm sur}}{2\rho _{0}} (\nabla \rho )^{2}+\\ &\ \frac{C_{\rm s}}{2\rho _{0}}\big[\rho ^{2}-\kappa _{\rm s}(\nabla \rho )^{2}\big]\delta ^{2} + g_{\tau}\frac{\rho ^{\eta +1}}{\rho_{0}^{\eta }}, \end{split} $$ (5) 式中,
$ \rho = \rho_{\rm n}+\rho_{\rm p} $ 是核子的密度。$ \delta = (\rho_{\rm n}-\rho_{\rm p})/ (\rho_{\rm n}+\rho_{\rm p}) $ 为同位旋不对称度。核相互作用势参数选用IQ2,见表1,其不可压缩系数$ K_{\infty} = 195 $ MeV。IQ2参数组被广泛应用于多核子转移反应研究,在描述58Ni+$ ^{208} {\rm{Pb}}$ 、$ ^{136} {\rm{Xe}}$ +$ ^{208} {\rm{Pb}}$ 、$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 和204Hg+$ ^{198} {\rm{Pt}}$ 等反应的产物截面上取得了很大的成功[13-14, 22, 29, 46]。表 1 IQ2参数组
参数 数值 $\alpha$/MeV –356 $\beta$/MeV 303 $\gamma$ 7/6 ${g}_{\rm sur}$/(MeV·fm2) 7.0 $g_{\tau}$/MeV 12.5 $\eta$ 2/3 $C_{\rm s}$/MeV 32.0 $\kappa_{\rm s}$/fm2 0.08 $\rho_{0}$/fm–3 0.165 在计算中,弹靶的初始距离设定为30 fm,反应演化时间为2 000 fm/c,时间步长为1 fm/c,碰撞参数
$ b = 0\sim 13 $ fm,总共模拟了3 120 000个事件。初始产物的退激过程采用统计模型GEMINI处理[47]。 -
图1给出了
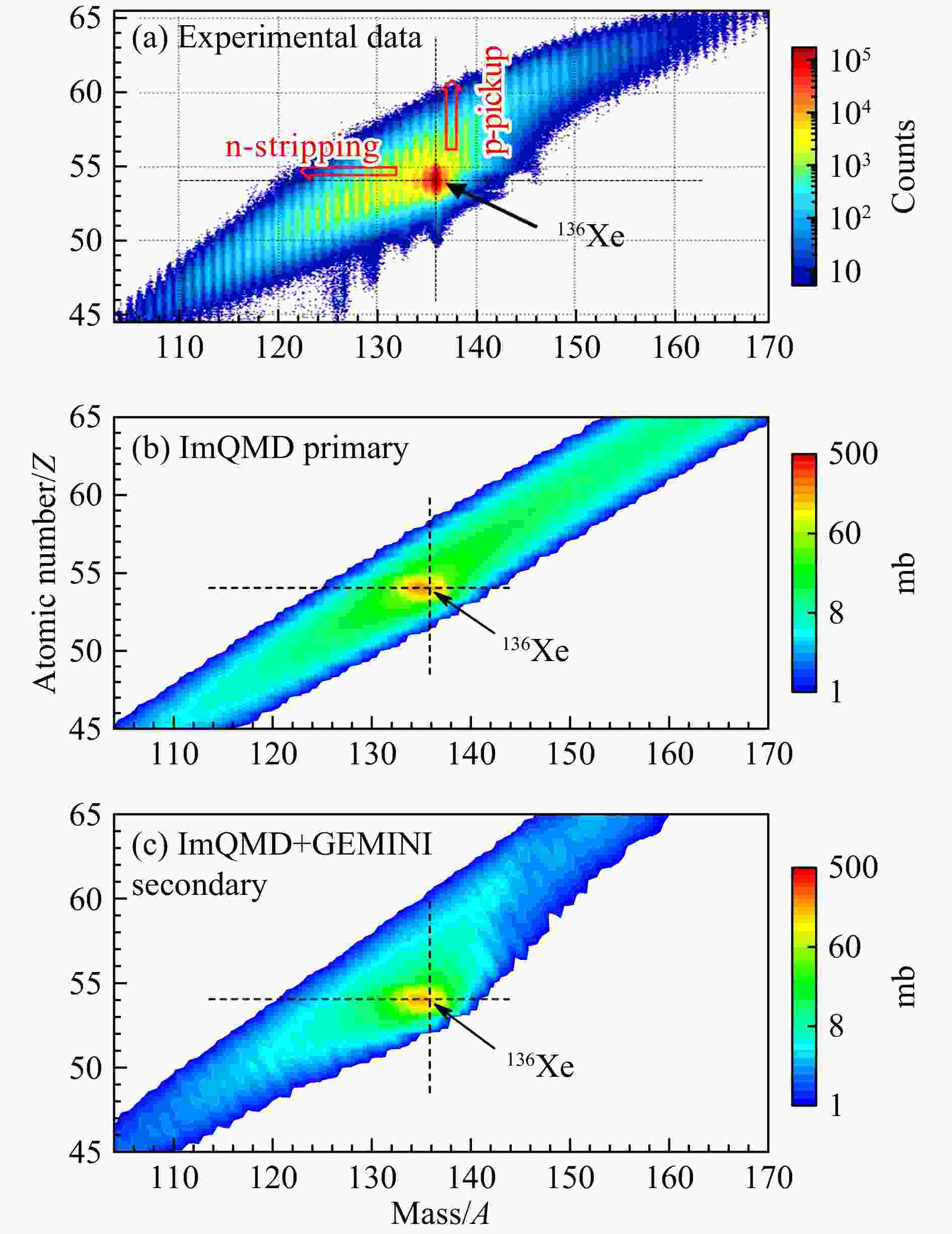
$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 在入射能量为7.98 MeV/nucleon下出射角为30°时类弹碎片(PLFs)的计数和截面分布。该反应中弹核的擦边角约为33°。图1(a)为实验测量的碎片的计数分布,图1(b)和1(c)分别为理论计算的类弹碎片的初始产生截面和最终截面分布。从图1(b)中可以看到,初始碎片主要集中在弹靶连线的两侧,近似呈对称分布,大部分初始碎片的产生截面在$ \sim10 $ mb量级。类弹碎片在退激过程中主要以中子蒸发为主。由图1(c)可知,退激发过程强烈地影响碎片的最终截面分布。尤其是位于弹核右上方具有较大质量转移的初始碎片只有很小的存活几率。因为这些碎片通常具有较高的激发能,大部分都经过中子蒸发向左平移到弹核附近。通过对比实验和理论的结果发现二者的分布非常相似,这表明ImQMD模型能较合理地描述多核子转移反应中的产物截面分布。多核子转移反应一般包含准弹性碰撞、深度非弹性碰撞和准裂变反应。为了弄清楚丰中子核产生于何种碰撞机制,我们首先采用反应时间来划分不同的反应机制。图2给出了
$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 反应中二分裂事件在不同弹靶接触时间下初始碎片的TKE-Mass分布。弹核的入射动能为1 085 MeV。接触时间定义为弹靶从接触到分离的时间间隔。在图2以及下文的计算中,产物的出射角均为$ 0^{\circ}\sim 180^{\circ} $ 。在图2(a)中,大部分事件的总动能接近于入射动能,体系的能量损失较少,弹靶间有少量的核子转移,这表明弹靶接触时间小于150 fm/c的碎片主要由准弹性碰撞机制产生。当150$ <t_{\rm con}\leqslant $ 500 fm/c时[图2(b)],大部分碎片的质量数接近弹核或靶核的质量数,但总动能损失较大,这类碎片主要由深度非弹性碰撞机制产生。当500$ <t_{\rm con}\leqslant $ 1 800 fm/c时[图2(c)],产物的TKE-Mass分布呈现出两端低中间高的趋势,产物的质量数主要介于弹靶的质量数之间,且体系的能量耗散很大,这是典型的准裂变事件特征。需要指出的是,由于涨落效应,各反应机制之间没有明显的时间界限,很难对其进行精确划分。在本文中,采用弹靶接触时间可以粗略地划分三种反应机制,即准弹性碰撞、深度非弹性碰撞和准裂变反应对应的弹靶接触时间范围分别为$ 0<t_{\rm con}\leqslant $ 150、150$ <t_{\rm con}\leqslant $ 500和500$ <t_{\rm con}\leqslant $ 1 800 fm/c。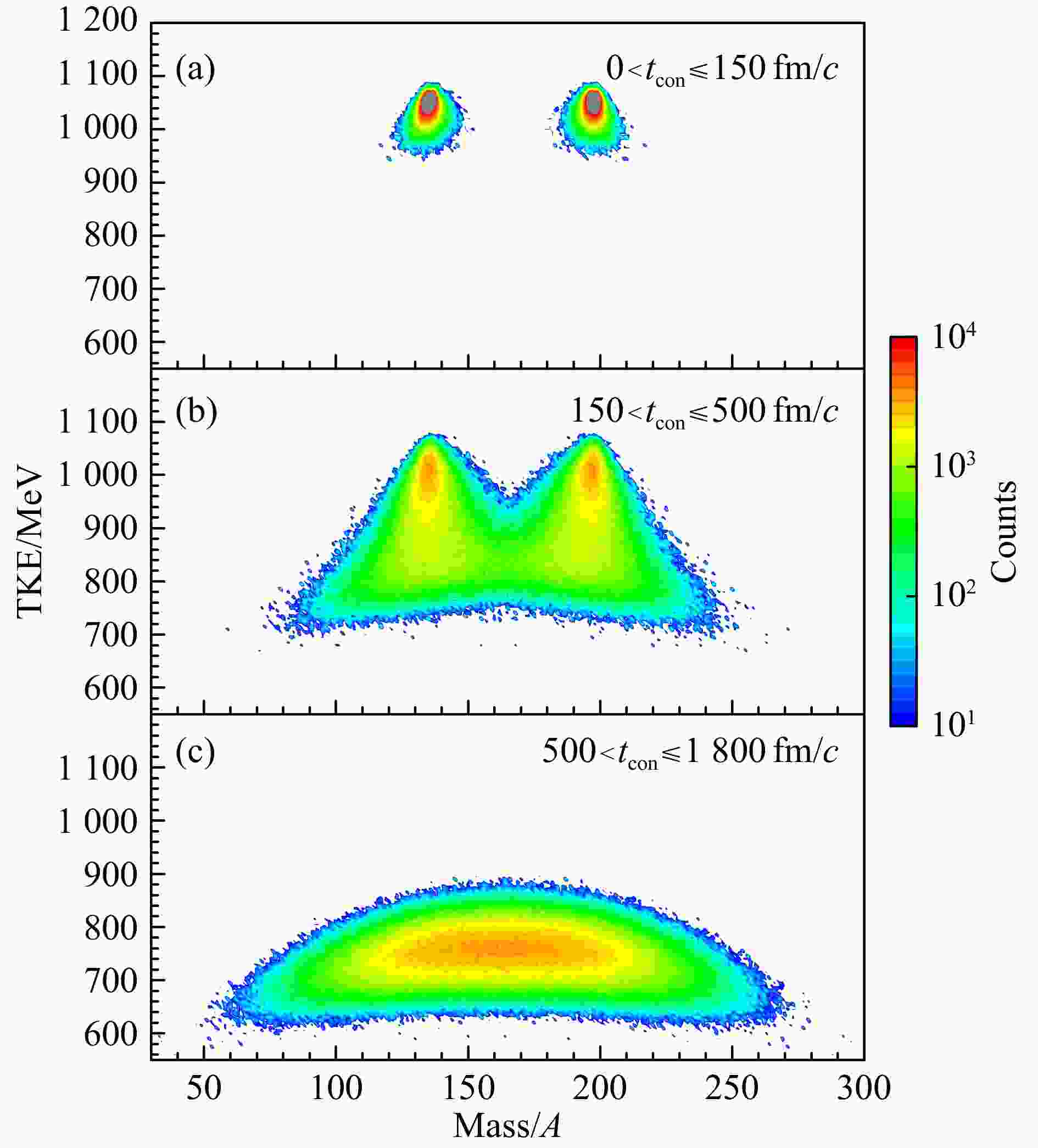
图 2 (在线彩图) ImQMD模型计算的
$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ 反应在弹靶接触时间分别为$0<t_{\rm con}\leqslant$ 150、$150< $ $ t_{\rm con}\leqslant$ 500和500$<t_{\rm con}\leqslant$ 1 800 fm/c下初始碎片的TKE-Mass分布图3给出了由ImQMD模型计算的不同弹靶接触时间下类靶产物(TLFs)的双微分截面。图3(a)主要为准弹性碰撞中类靶产物的双微分截面分布,大部分产物的出射角位于
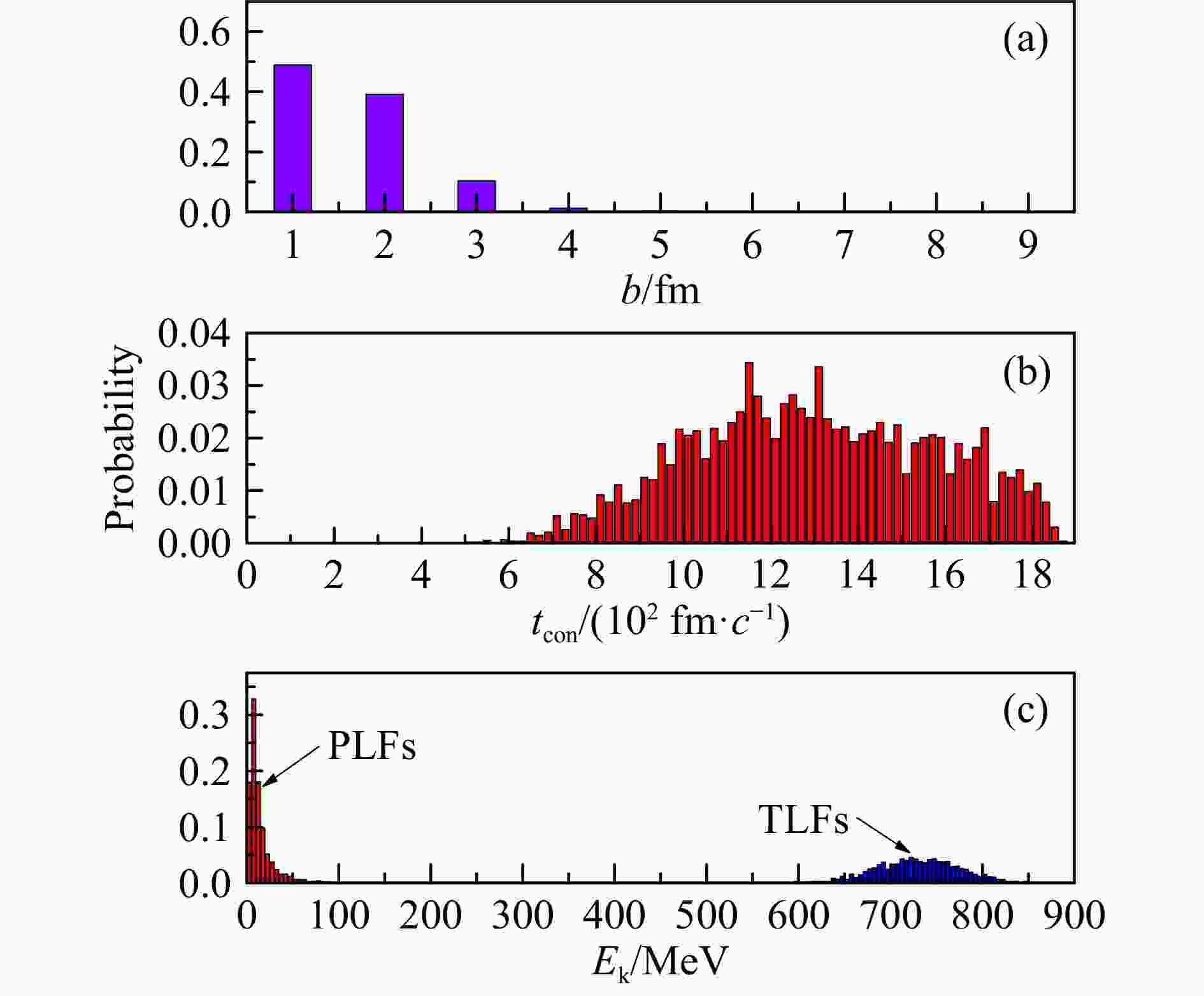
$ 60^{\circ}\sim 70^{\circ} $ ,出射动能位于100$ \sim 200$ MeV之间;图3(b)主要为深度非弹性碰撞中类靶产物的双微分截面分布,大部分产物(红色区域)的出射角位于$45 ^{\circ}\sim 65^{\circ} $ 之间,动能也主要位于100$ \sim 200$ MeV之间;图3(c)主要为准裂变过程中类靶产物的双微分截面分布,这类产物的分布范围较大,主要集中于$ 0^{\circ}\sim 80^{\circ} $ 和50$ \sim 800 $ MeV区域。从图中可以看到,产物的出射动能随着出射角的减小迅速增大,在$0 ^{\circ} $ 角附近,类靶碎片的最大出射动能超过了800 MeV。近年来,$0 ^{\circ} $ 角附近的多核子转移反应产物测量已受到国内外实验核物理学家的关注,其发射机制有待澄清。为了理解0°附近碎片的来源,图4给出了类靶碎片在出射角为$ 0^{\circ}\sim 5^{\circ} $ 时,反应事件的碰撞参数分布、弹靶接触时间分布和碎片动能分布。我们发现,对于$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 体系,$ 0^{\circ} $ 出射角附近的碎片主要来源于中心碰撞[见图4(a)],弹靶的接触时间大于600 fm/c[见图4(b)]。在碰撞过程中,弹核将绝大部分入射动能传递给靶核,导致类弹碎片的出射动能通常小于50 MeV[见图4(c)]。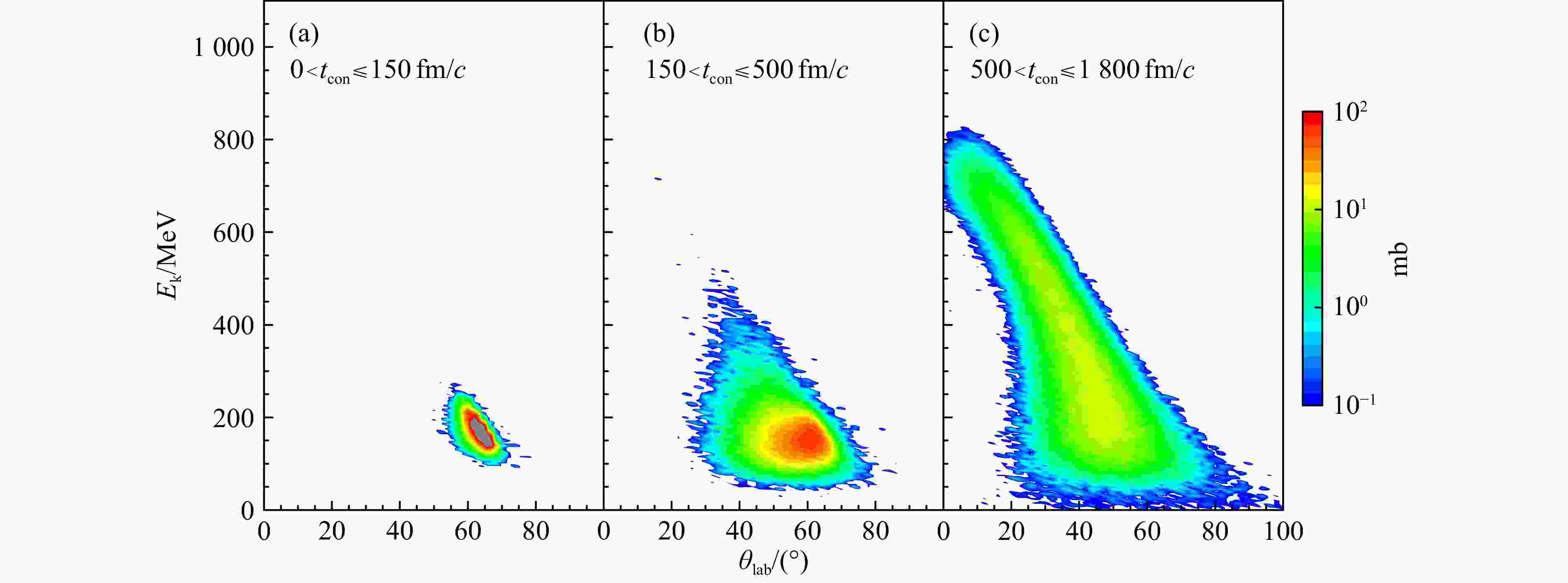
图 3 (在线彩图) 在弹靶接触时间为0
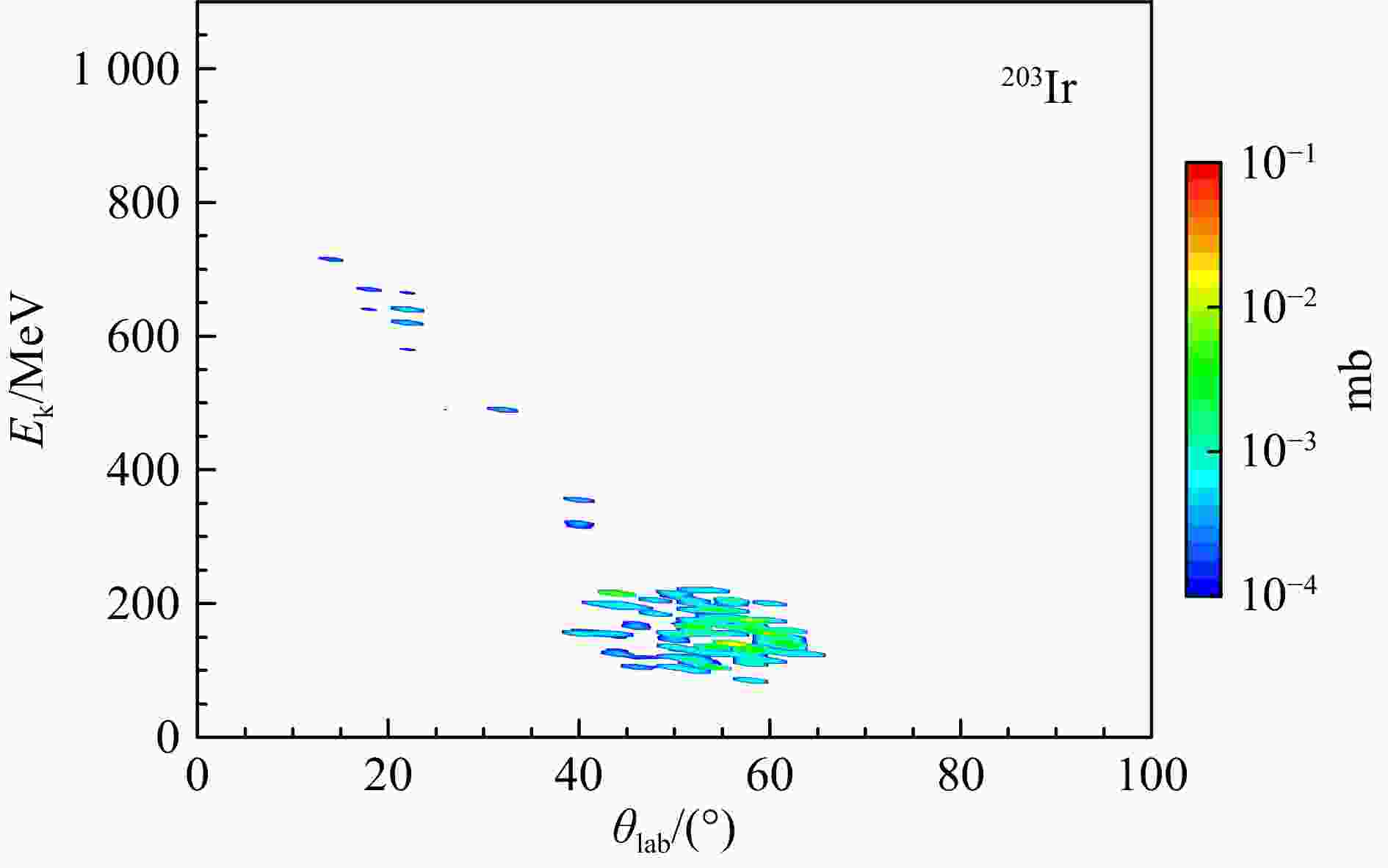
$<t_{\rm con}\leqslant$ 150、150$<t_{\rm con}\leqslant$ 500和500$<t_{\rm con}\leqslant$ 1 800 fm/c下所有类靶产物的双微分截面分布根据三种反应机制所对应的产物双微分截面分布,我们也可以根据产物的双微分截面分布反推它的产生机制。图5给出了理论计算的丰中子类靶产物
$ ^{203}{\rm{Ir}} $ 的双微分截面。从图中可以发现,$ ^{203}{\rm{Ir}} $ 的出射角主要位于$40 ^{\circ}\sim 65^{\circ} $ 之间,出射动能主要位于$100\sim 200$ MeV之间,这是典型的深度非弹性碰撞产物的双微分截面分布特征[见图3(b)],这表明丰中子类靶核产生于深度非弹性碰撞。为了进一步证实丰中子核的产生机制,图6给出了不同弹靶接触时间以及不同总动能损失情况下Ba(
$ Z = 56 $ )的同位素最终产生截面分布。从图6(a)可以看到,在准弹性碰撞过程中($ 0<t_{\rm con}\leqslant $ 150 fm/c),丰中子核的截面较低,因为在准弹性碰撞过程中弹靶间转移的核子数较少,产生丰中子核的几率很低。准裂变反应过程(500$ <t_{\rm con}\leqslant $ 1 800 fm/c)也不适合产生丰中子核,因为准裂变产物的激发能较高,产物在退激的过程中将蒸发大量的中子。而在深度非弹性碰撞中(150$ <t_{\rm con}\leqslant $ 500 fm/c),丰中子核的最终产生截面最大,因为丰中子核的初始截面相对较大,而激发能又相对较低,受激发的丰中子核只需要蒸发较少的中子就能达到基态。图6(b)给出了实验测量的不同总动能损失(TKEL)下的Ba同位素产生截面。由于实验数据只包含出射角为$ 30^{\circ} $ (擦边角为$33^{\circ} $ )的类弹碎片,因而测量的Ba同位素分布的宽度比理论计算的宽度窄很多。对于$ -25< $ $ {\rm TLEL}\leqslant 25 $ MeV的事件,体系的能量损失很小,反应主要为准弹性碰撞,因此丰中子核的产生截面较低。当$ 25<{\rm TLEL}\leqslant 125 $ MeV时,丰中子核的产生截面最大,因为深度非弹性碰撞事件占主导(在$ ^{136} {\rm{Xe}}$ +$ ^{208} {\rm{Pb}}$ 反应中,准弹性碰撞事件中TKEL的值一般小于40 MeV,见文献[41])。随着体系的总动能损失持续增加,反应机制将逐渐演变为准裂变反应,因此丰中子核的产生截面迅速降低。通过对比实验给出的不同TKEL下和理论计算的不同弹靶接触时间下的同位素截面分布,我们发现二者得到的结论是一致的,即丰中子核主要产生于深度非弹性碰撞。因为体系的TKEL大小和弹靶接触时间长短之间具有一定的正相关性,一般而言,弹靶接触时间越长体系的TKEL值越大,见文献[49]。需要指出的是,准弹性碰撞、深度非弹性碰撞和准裂变反应机制之间并没有清晰的界限,不论是通过弹靶接触时间还是通过总动能损失都很难对这三种反应机制进行严格的划分。 -
本文研究了
$ ^{136} {\rm{Xe}}$ +$ ^{198} {\rm{Pt}}$ 在入射能量为7.98 MeV/nucleon下的多核子转移反应过程。对比了理论计算的类弹碎片的产生截面分布和实验测量的计数分布,发现ImQMD模型能较好地描述多核子转移反应中的产物截面分布。通过弹靶接触时间对准弹性碰撞、深度非弹性碰撞和准裂变反应机制进行了划分,这三种反应机制对应的弹靶接触时间范围分别为$ 0<t_{\rm con}\leqslant $ 150、150$ <t_{\rm con}\leqslant $ 500和500$ <t_{\rm con}\leqslant $ 1 800 fm/c。分析了不同弹靶接触时间下类靶产物的双微分截面分布和Ba同位素截面分布,发现丰中子核产生于深度非弹性碰撞机制。因此,在实验上通过多核子转移反应合成丰中子新核素时,为了获得较大的丰中子核产生截面,需要找到最佳的入射能量以提高深度非弹性碰撞事件的概率。另外通过分析发现,$0 ^{\circ} $ 附近出射的类靶碎片来源于中心碰撞,且具有较高的出射动能。这将为实验上开展$ 0^{\circ} $ 角附近的碎片测量提供有意义的参考。
Study on Production Mechanism of the Neutron-rich Nuclei in Multinucleon Transfer Reactions via Reaction Time Analysis
-
摘要: 在改进的量子分子动力学(ImQMD)模型框架下,研究了
$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ 体系的多核子转移反应过程。给出了不同弹靶接触时间下二分裂碎片的总动能-质量分布,发现准弹性碰撞、深度非弹性碰撞和准裂变反应事件可以采用弹靶接触时间进行粗略的划分。分析了不同弹靶接触时间下类靶碎片的双微分截面分布以及Ba同位素的产生截面分布,结果表明丰中子核素产生于深度非弹性碰撞。另外研究发现,对于$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ 体系,出射角在0°附近的类靶碎片产生于中心碰撞。Abstract: The multinucleon transfer reaction processes of$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ are investigated by using the ImQMD model. The TKE-Mass distributions of binary fragments at different contact time scales are analysed. It is found that the quasielastic collisions, the deep-inelastic collisions and the quasifission reactions can be roughly distinguished by the contact time. By analysing the double differential cross sections of the TLFs and the isotopic cross sections of Ba nuclei under the different contact time, we find that the neutron-rich nuclei are produced in the deep-inelastic collisions. In addition, the TLFs with emission angle around 0° are produced in central collisions for the reactions of$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ . -
图 1 (在线彩图)
$^{136}{\rm{Xe}}$ +$^{198}{\rm{Pt}}$ 在入射能量为7.98 MeV/nucleon下与束流方向夹角为30°时类弹碎片的计数和截面分布(a)为实验数据,取自文献[48];(b)和(c)分别为ImQMD和ImQMD+GEMINI模型的计算结果。
图 6 (在线彩图) 类弹产物Ba( Z=56 )的同位素产生截面分布
(a)为ImQMD+GEMINI模型计算的不同弹靶接触时间下的同位素产生截面;(b)为实验测量的不同总动能损失下的同位素产生截面,测量角度为30°,实验数据取自文献[50]。
表 1 IQ2参数组
参数 数值 $\alpha$/MeV –356 $\beta$/MeV 303 $\gamma$ 7/6 ${g}_{\rm sur}$/(MeV·fm2) 7.0 $g_{\tau}$/MeV 12.5 $\eta$ 2/3 $C_{\rm s}$/MeV 32.0 $\kappa_{\rm s}$/fm2 0.08 $\rho_{0}$/fm–3 0.165 -
[1] THOENNESSEN M. The Discovery of Isotopes, A Complete Compilation[M]. New York: Springer International Publishing, 2016. [2] THOENNESSEN M, SHERRILL B. Nature, 2011, 473: 25. doi: 10.1038/473025a [3] Discovery of Nuclides Project [EB/OL].[2020-07-10].https://people.nscl.msu.edu/thoennes/isotopes/. [4] WANG N, LIU M, WU X Z, et al. Phys Lett B, 2014, 734: 215. doi: 10.1016/j.physletb.2014.05.049 [5] MÖLLER P, NIX J R, MYERS W D, et al. At Data Nucl Data Tables, 1995, 59: 185. doi: 10.1006/adnd.1995.1002 [6] ERLER J, BIRGE N, KORTELAINEN M, et al. Nature (London), 2012, 486: 509. doi: 10.1038/nature11188 [7] KURCEWICZ J, FARINON F, GEISSEL H, et al. Phys Lett B, 2012, 717: 371. doi: 10.1016/j.physletb.2012.09.021 [8] FUKUDA N, KUBO T, KAMEDA D, et al. J Phys Soc Jpn, 2018, 87: 014202. doi: 10.7566/JPSJ.87.014202 [9] SHIMIZU Y, KUBO T, FUKUDA N, et al. J Phys Soc Jpn, 2018, 87: 014203. doi: 10.7566/JPSJ.87.014203 [10] ZAGREBAEV V I, GREINER W. Phys Rev Lett, 2008, 101: 122701. doi: 10.1103/PhysRevLett.101.122701 [11] ZHANG F S, LI C, ZHU L, et al. Front Phys, 2018, 13: 132113. doi: 10.1007/s11467-018-0843-6 [12] ZHU L, LI C, GUO C C, et al. Int J Mod Phys E, 2020, 29: 2030004. doi: 10.1142/S0218301320300040 [13] LI C, XU X X, LI J J, et al. Phys Rev C, 2019, 99: 024602. doi: 10.1103/PhysRevC.99.024602 [14] LI C, SOKHNA C A T, XU X X, et al. Phys Rev C, 2019, 99: 034619. doi: 10.1103/PhysRevC.99.034619 [15] BAO X J, GUO S Q, LI J Q, et al. Phys Lett B, 2018, 785: 221. doi: 10.1016/j.physletb.2018.08.049 [16] ZHU L. Chin Phys C, 2017, 41: 124102. doi: 10.1088/1674-1137/41/12/124102 [17] ZHU L. Chin Phys C, 2019, 43: 124103. doi: 10.1088/1674-1137/43/12/124103 [18] CHEN P H, NIU F, ZUO W, et al. Phys Rev C, 2020, 101: 024610. doi: 10.1103/PhysRevC.101.024610 [19] GUO S Q, BAO X J, ZHANG H F, et al. Phys Rev C, 2019, 100: 054616. doi: 10.1103/PhysRevC.100.054616 [20] JIANG X, WANG N. Phys Rev C, 2020, 101: 014604. doi: 10.1103/PhysRevC.101.014604 [21] MUN M H, ADAMIAN G G, ANTONENKO N V, et al. Phys Rev C, 2015, 91: 054610. doi: 10.1103/PhysRevC.91.054610 [22] LI C, WEN P W, LI J J, et al. Phys Lett B, 2018, 776: 278. doi: 10.1016/j.physletb.2017.11.060 [23] WANG N, GUO L. Phys Lett B, 2016, 760: 236. doi: 10.1016/j.physletb.2016.06.073 [24] ZHAO K, LIU Z, ZHANG F S, et al. Phys Lett B, 2021, 815: 136101. doi: 10.1016/j.physletb.2021.136101 [25] ZHU L. Phys Lett B, 2021, 816: 136226. doi: 10.1016/j.physletb.2021.136226 [26] LI C, TIAN J L, ZHANG F S. Phys Lett B, 2020, 809: 135697. doi: 10.1016/j.physletb.2020.135697 [27] 赵凯, 夏政通, 段济正. 原子核物理评论, 2020, 37: 160. doi: 10.11804/NuclPhysRev.37.2020022 ZHAO K, XIA Z T, DUAN J Z. Nuclear Physics Review, 2020, 37: 160. (in Chinese) doi: 10.11804/NuclPhysRev.37.2020022 [28] 蒋翔, 王楠. 原子核物理评论, 2021, 38: 17. doi: 10.11804/NuclPhysRev.38.2020076 JIANG X, WANG N. Nuclear Physics Review, 2021, 38: 17. (in Chinese) doi: 10.11804/NuclPhysRev.38.2020076 [29] WELSH T, LOVELAND W, YANEZ R, et al. Phys Lett B, 2017, 771: 119. doi: 10.1016/j.physletb.2017.05.044 [30] BARRETT J S, LOVELAND W, YANEZ R, et al. Phys Rev C, 2015, 91: 064615. doi: 10.1103/PhysRevC.91.064615 [31] WATANABE Y X, KIM Y H, JEONG S C, et al. Phys Rev Lett, 2015, 115: 172503. doi: 10.1103/PhysRevLett.115.172503 [32] BELIUSKINA O, HEINZ S, ZAGREBAEV V I, et al. Eur Phys J A, 2014, 50: 161. doi: 10.1140/epja/i2014-14161-3 [33] MIJATOVIć T, SZILNER S, CORRADI L, et al. , Phys Rev C, 2016, 94: 064616. doi: 10.1103/PhysRevC.94.064616 [34] CORRADI L, POLLAROLO G, SZILNER S. J Phys G Nucl Part Phys, 2009, 36: 113101. doi: 10.1088/0954-3899/36/11/113101 [35] VOGT A, BIRKENBACH B, REITER P, et al. Phys Rev C, 2015, 92: 024619. doi: 10.1103/PhysRevC.92.024619 [36] DESAI V V, LOVELAND W, MCCALEB K, et al. Phys Rev C, 2019, 99: 044604. doi: 10.1103/PhysRevC.99.044604 [37] DESAI V V, LOVELAND W, YANEZ R, et al. Eur Phys J A, 2020, 56: 150. doi: 10.1140/epja/s10050-020-00154-4 [38] REJMUND M, LECORNU B, NAVIN A, et al. Nucl Instr and Meth A, 2011, 646: 184. doi: 10.1016/j.nima.2011.05.007 [39] KOZULIN E M, KNYAZHEVA G N, DMITRIEV S N, et al. Phys Rev C, 2014, 89: 014614. doi: 10.1103/PhysRevC.89.014614 [40] ITKIS I M, KOZULIN E M, ITKIS M G, et al. Phys Rev C, 2011, 83: 064613. doi: 10.1103/PhysRevC.83.064613 [41] KOZULIN E M, VARDACI E, KNYAZHEVA G N, et al. Phys Rev C, 2012, 86: 044611. doi: 10.1103/PhysRevC.86.044611 [42] AICHELIN J. Phys. Rep., 1991, 202: 233. doi: 10.1016/0370-1573(91)90094-3 [43] WANG N, LI Z X, WU X Z. Phys Rev C, 2002, 65: 064608. doi: 10.1103/PhysRevC.65.064608 [44] WANG N, LI Z X, WU X Z, et al. Phys Rev C, 2004, 69: 034608. doi: 10.1103/PhysRevC.69.034608 [45] ZHANG Y X, WANG N, LI Q F, et al. Front Phys, 2020, 15: 54301. doi: 10.1007/s11467-020-0961-9 [46] LI C, ZHANG F, LI J J, et al. Phys Rev C, 2016, 93: 014618. doi: 10.1103/PhysRevC.93.014618 [47] CHARITY R J. Phys Rev C, 2010, 82: 014610. doi: 10.1103/PhysRevC.82.014610 [48] WATANABE Y X, HIRAYAMA Y, IMAI N, et al. Nucl Instr and Meth B, 2013, 317: 752. doi: 10.1016/j.nimb.2013.04.036 [49] YAO H, WANG N. Phys Rev C, 2017, 95: 014607. doi: 10.1103/PhysRevC.95.014607 [50] KIM Y H, WATANABE Y X, HIRAYAMA Y, et al. EPJ Web of Conf, 2014, 66: 3044. doi: 10.1051/epjconf/20146603044 -










 下载:
下载:

































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号