-
离子源作为离子加速器的离子产生注入器,是加速器装置中最为关键的环节之一。随着加速器用户群体对加速器束流要求的提高,加速器对离子源引出束流的流强、品质等也提出了更高的要求。离子源引出束流流强的增加会直接导致低能传输线中的空间电荷效应的加剧,造成束流包络变大、投影发射度增长等影响束流传输与束流品质的问题[1]。幸运的是,离子束在经过束流传输管道时,会与管道内残余的中性气体发生电离反应等,产生二次电子与二次离子[2-3]。其中,二次离子会在主离子束形成的空间电势作用下被向外排斥,而二次电子则会被空间电势约束,形成对主离子束空间电荷的部分中和,从而实现一定程度的空间电荷补偿。
空间电荷补偿度(Space Charge Compensation Degree, SCCD) 是影响低能强流离子束流传输模拟的一个重要参数,包括IMP[4]、PKU[5]、CEA-Saclay[6-7]、MSU[8]等国内外大学和研究机构都曾针对不同流强和粒子种类离子束的SCCD开展过一系列的测量与研究。离子束的SCCD
$ {\eta } $ 定义为$$ \eta = 1-\frac{\Delta\phi_{\rm{c}}}{\Delta\phi_{\rm{un}}} =1-\frac{\phi_{\rm{c, \, center}}-\phi_{\rm{c, \, edge}}}{\phi_{\rm{un, \, center}}-\phi_{\rm{un, \, edge}}}, $$ (1) 其中:
$ {\phi_{\rm{c, \, center}}} $ 和$ {\phi_{\rm{c, \, edge}}} $ 分别是已被补偿的离子束束流中心和束流边界的电势;而$ {\phi_{\rm{un, \, edge}}} $ 和$ {\phi_{\rm{un, \, center}}} $ 分别是未被补偿的离子束束流中心和束流边界的电势。一般认为离子束与中性气体发生电离反应生成的二次粒子初始能量可以忽略不计,那么被排斥出主离子束的二次离子能量则全部来自空间电势能。因此我们可以通过测量二次离子的能量分布来对应得到主离子束的空间电势分布,从中即可得出已补偿的离子束从束流中心到束流边界的空间电势差$ {\Delta\phi_{\rm{c}}} $ 。而对于未被补偿的离子束从束流中心到束流边界的空间电势差$ {\Delta\phi_{\rm{un}}} $ 值的获取,在之前的研究中通常假定离子束为均匀分布的柱状束,根据高斯定理可以得到与束流中心距离为$ {r} $ 处的空间电场强度$ {E(r)} $ 为$$ \begin{array}{l} E(r)= \left\{ \begin{aligned} \frac{Ir}{2\pi\varepsilon^{}_{0}r_{\rm b}^{2}v} , \;\;\;\;\; r \leqslant r_{\rm b}, \\ \frac{I} {2\pi\varepsilon^{}_{0}rv} , \;\;\;\;\; r>r^{}_{\rm b}。 \end{aligned} \right. \end{array} $$ (2) 其中:
$ {\varepsilon_{0}} $ 为真空介电常数;$ {r_{\rm b}} $ 为离子束的半径;$ {I} $ 和$ {v} $ 分别是离子束的总流强和速度。通过对式(2)积分即可得到$ {\Delta\phi_{\rm{un}}} $ 为$$ {\Delta\phi_{\rm{un}}} = \frac{I} {4\pi\varepsilon_{0}v}。 $$ (3) 然而,对于从ECR(Electron Cyclotron Resonance)离子源引出的离子束,特别是还未经过分析磁铁的混合电荷态离子束来说,在离子源六极磁场和轴向磁场等因素的作用下,束流分布是既不均匀也不规则的。通过式(3)计算得出的
$ {\Delta\phi_{\rm{un}}} $ 计算值与实际值会有巨大的误差,导致束流SCCD的测量结果不准确。因此,为了准确测量混合离子束的SCCD,我们需要得到离子束的剖面电流分布,从而根据电势叠加原理计算得出离子束剖面的空间电势分布。本文将利用一台三栅网式能量分析仪(Three-grid Energy Analyzer, TEA)[4]和一台束流剖面探测器(Beam Profile Monitor, BPM)[9],系统测量从SECRAL(Superconducting ECR ion source with Advanced design in Lanzhou)[10]离子源引出的混合O离子束的SCCD。
-
SECRAL离子源是中国科学院近代物理研究所研发的第三代高性能超导ECR离子源,于2005年首次出束。其最高轴向磁场可达3.6 T,弧腔内壁的最高径向场可达2.0 T,常用馈入微波频率在
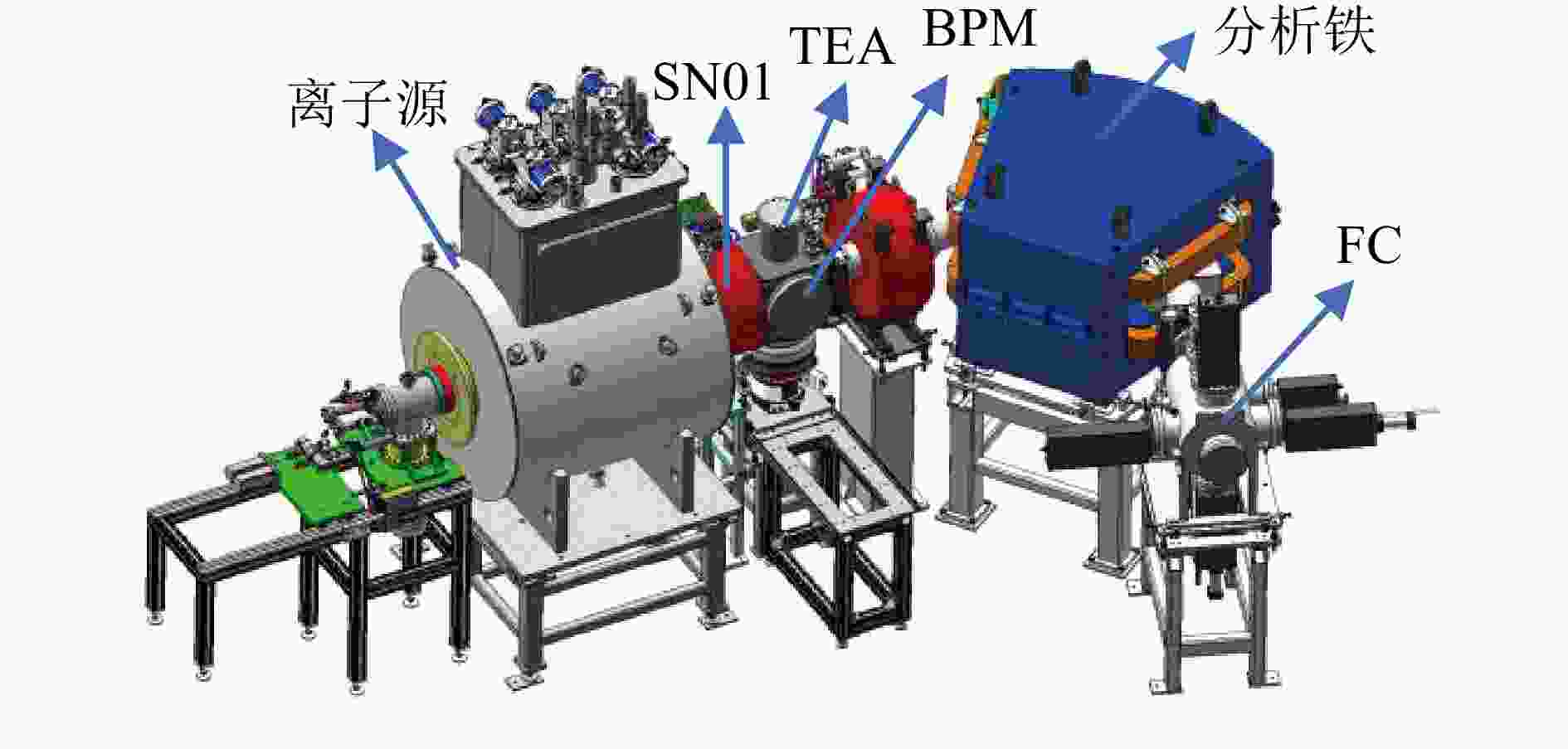
$ {18} \sim {28} $ GHz之间[11-12]。目前该离子源安装在LEAF(Low Energy high intensity heavy ion Accelerator Facility)平台,作为LEAF平台直线加速器的注入器[13]。SECRAL离子源及LEBT的布局如图1所示。TEA和BPM分别安装在离子源引出端第一个聚焦螺线管(SN01)之后的方型诊断室的顶部和侧面法兰。通过调节SN01的电流大小,可以改变混合束在方型诊断室处的束流剖面流强分布。束流的电荷态分布可由分析铁和后端的法拉第筒(Faraday Cup, FC)测量得到。 -
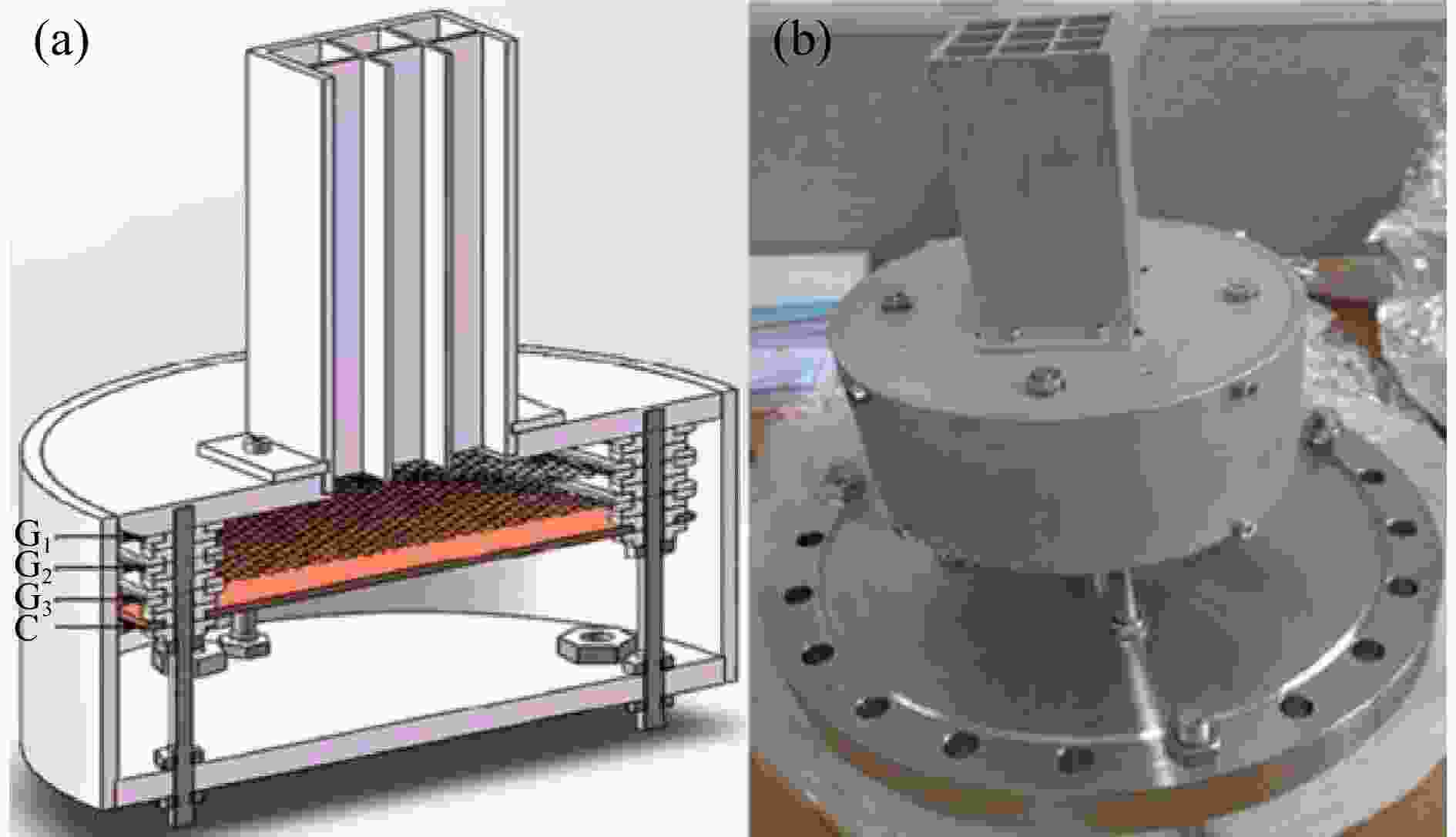
TEA 的示意图如图2所示。TEA主要由准直系统、三个互相平行的栅网(G1、G2、G3)和一个收集板C组成。准直系统包括9个面积均为1 cm2、长度均为79 mm的正方形准直孔,从而限制只有入射角在
$-10.15^{\circ} \sim 10.15^{\circ}$ 之间的粒子可以通过。三个栅网之间互相绝缘,均选用高离子通过率的精细铜质栅网,以减少二次离子在栅网上的损失。其中,G1接地以在G1和G2之间形成二次离子的均匀减速场,G2接正电压以筛选出能量高于设定阈值的二次离子,G3接负偏压(通常设置−300 V)以阻止入射的二次电子通过以及收集板上产生的二次电子射出。收集板C通过同轴电缆与Keithley 6485型号的皮安表相连,以测量通过准直系统和栅网筛选的二次离子流强。扫描G2的电压并记录皮安表的流强值,即可得到二次离子能谱,也可得到$ {\Delta\phi_{\rm{c}}} $ 。 -
BPM的示意图如图3所示。BPM主要由一维位置灵敏探测器、高精度线性驱动装置和数据获取与处理系统构成[14]。一维位置灵敏探测器共有128个通道,分别与128通道的皮安表系统相连,彼此相互独立并均匀分布在90 mm长的竖直线段上。每个通道的皮安表量程都可以根据入射束流强度来进行调节。探测器入口处装有一个水平缝宽0.2 mm、竖直缝长90 mm的金属狭缝,用以限制进入探测器的束流。该狭缝可以有效减小在探测器阳极上沉积的束流能量,同时还确定了探测器在水平方向的分辨率。狭缝上还接负偏压(通常设置为−500 V)以降低二次电子对探测器测量的影响。测量时,探测器由高精度线性驱动装置控制沿水平方向进行扫描,可测量的剖面面积为
$90\; {\rm mm} \times 90\; {\rm mm}$ ,在水平、竖直方向上的分辨率分别约为0.2和0.7 mm。每次测量完成后,数据获取与处理系统都会得到一个大小为${128 \times 447}$ 的二维流强分布矩阵,即为束流剖面流强分布。束流剖面电势分布可由二维流强分布矩阵计算得出。首先,通过计算矩阵中所有元素的和与实际束流总流强进行校准,可以得到任意矩阵元素
$ {j} $ 处的实际电流值$ {I_{j}} $ 。那么任意矩阵元素$ {i}({i{\neq}j} $ )处的电势$ {\phi_{i}} $ 即可根据电势叠加原理,由下式计算得出:$$ \phi_{i}=\sum\limits_{i{\neq}j}\frac{I_{j}}{2\pi\varepsilon_{0}v}\ln\frac{d_{j{\leftrightarrow}0}}{d_{j{\leftrightarrow}i}}, $$ (4) 其中:
$ {d_{j{\leftrightarrow}0}} $ 表示从元素$ {j} $ 处到电势为0的束流管道之间的距离;$ {d_{j{\leftrightarrow}i}} $ 表示从元素$ {j} $ 处到元素$ {i} $ 处的距离;$ {v} $ 表示离子束的速度。对于混合O离子束来说,在同一引出高压下,每种电荷态的O离子速度是互不相同的。我们可以根据后端FC测到的束流电荷态流强分布,对每种电荷态的离子速度进行加权计算,得出混合O离子束的平均速度:$$ v=I_{{\rm{total}}}\Big{/}{\sum\frac{I_{q}}{v_{q}}} , $$ (5) 其中:
$ {I_{\rm{total}}} $ 表示混合O离子束的总流强;$ {I_{q}} $ 和$ {v_{q}} $ 分别表示电荷态为$ {q} $ 的O离子的流强和速度。根据上述式(4)、(5)对所测混合束流的二维流强分布矩阵进行计算,即可得到束流的二维电势分布矩阵。再结合BPM所测到的束斑轮廓,可分别获取束流中心和束流边界所在的位置信息,从而得到$ {\Delta\phi_{\rm{un}}} $ 。 -
在SECRAL离子源引出系统后的混合束传输段,在引出高压HV为15 kV、聚焦螺线管SN01电流为150, 200, 250 A的情况下,对总流强为1.01, 2.02, 3.02, 4.02, 5.07, 6.02, 7.04 emA的混合O离子束,分别测量了束流的二次离子能量分布和束流剖面的电流分布,从中可分别得出
$ {\Delta\phi_{\rm{c}}} $ 和$ {\Delta\phi_{\rm{un}}} $ ,再利用式(1)即可计算得到对应束流的SCCD。在SN01电流为150 A时,对于总流强$ {1} \sim {7} $ emA的引出束流,图1中方型诊断室处的真空度变化范围在9.8×10−6~1.4×10−5 Pa之间,因此,真空度的差异对空间电荷补偿度的影响可以忽略,在此不作讨论。由于本次实验中TEA装配在方型诊断室的顶部,因此下文所述$ {\Delta\phi_{\rm{c}}} $ 和$ {\Delta\phi_{\rm{un}}} $ 均指的是束流中心到束流垂直方向上方边界的电势差。 -
总流强1.01 emA的混合O离子束在不同SN01电流值下的二次离子能量分布如图4所示。其中
$ x $ 轴表示栅网G2上加载的扫描电压,$ y $ 轴表示收集板C连接的皮安表测得的电流值。图4中三条曲线的基准线不一致可能是由于当束斑较大时部分束流直接轰击在TEA的准直孔或者管道壁上,产生了较高能量(>100 eV)的二次离子,这些二次离子通过散射穿过准直孔而被极板收集,使最终二次离子量分布的曲线基准线升高。不过这些因素只会造成所测二次离子能量分布曲线在
$ y $ 方向上的平移,不会改变$ {\Delta\phi_{\rm{c}}} $ 值的大小。对不同SN01下测得的每条曲线微分,之后分别进行高斯拟合,即可得到不同SN01下的二次离子能谱,如图5所示。从图5中可知,SN01 150, 200, 250 A时,二次离子能谱的半高宽分别约为4.4, 17.3, 12.8 V,即对应离子束的
$ {\Delta\phi_{\rm{c}}} $ ,而拟合产生的误差分别约为1.2, 3.5, 2.4 V。 -
总流强1.01 emA的混合O离子束在SN01为150, 200和250 A时的束流剖面分布如图6所示。其中图6(a)~(c)代表束流剖面的电流分布,图6(d)~(f)代表束流剖面的电势分布。从图6中可知,SN01为150, 200, 250 A时,对应离子束的
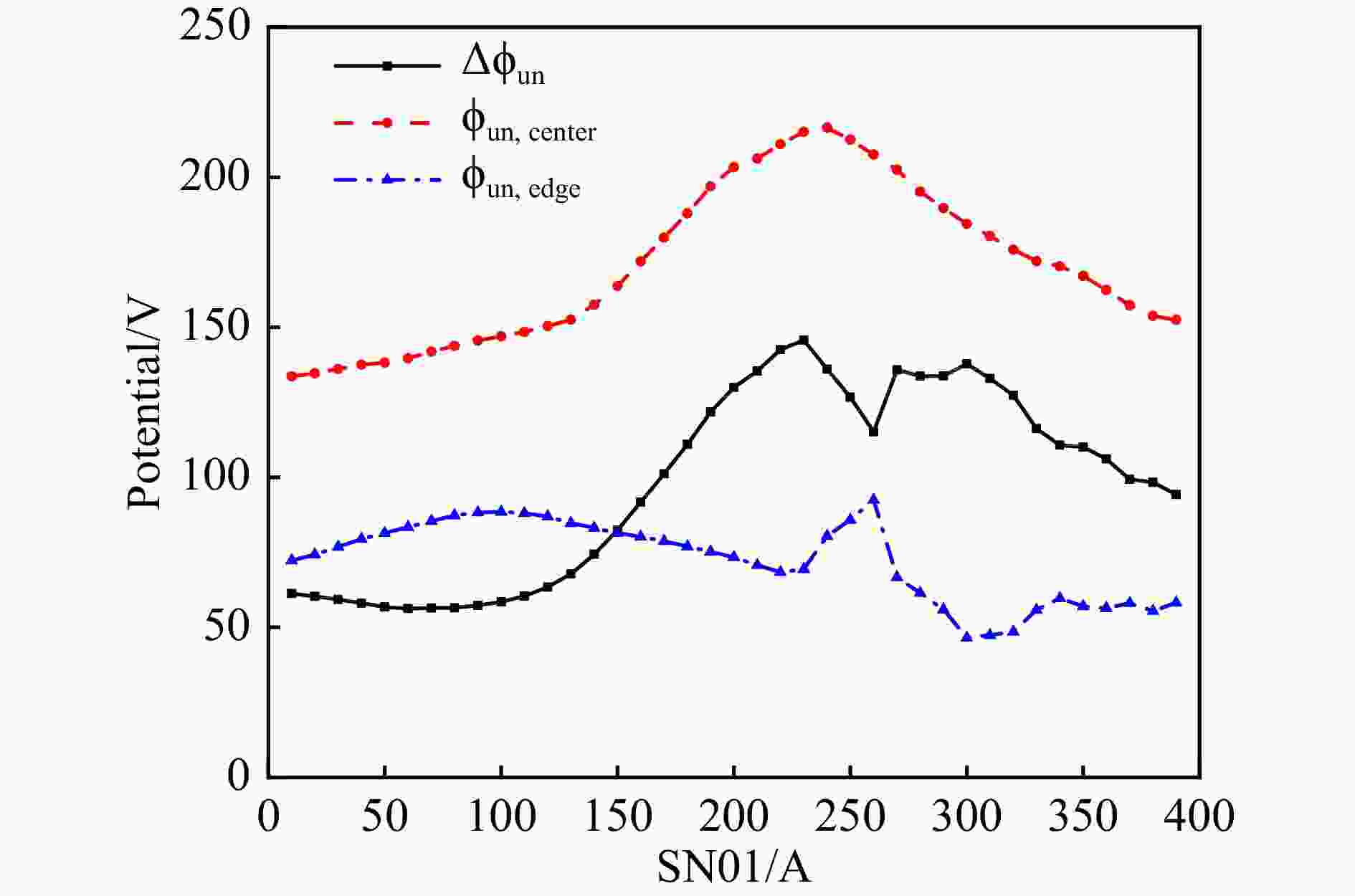
$ {\Delta\phi_{\rm{un}}} $ 分别为21.9, 31.4, 37.0 V。总流强4.02 emA的混合O离子束在不同SN01电流值下的束流剖面电势分布如图7所示。可以看到,随着束流形状和电流分布的改变,束流的电势分布以及
$ {\Delta\phi_{\rm{un}}} $ 也有非常明显的变化。随着SN01电流值的逐渐增加,$ {\phi_{\rm{un, \, edge}}} $ 的变化相对较小,而$ {\phi_{\rm{un, \, center}}} $ $ {\Delta\phi_{\rm{un}}} $ 均呈现先增大后减小的趋势。在SN01=230 A左右,$ {\phi_{\rm{un, \, center}}} $ 和$ {\Delta\phi_{\rm{un}}} $ 达到最大值,分别为216.5 和145.7 V。 -
在SN01=150 A下,根据实际电流分布模型和采用简单柱状均匀分布模型计算得到的总流强
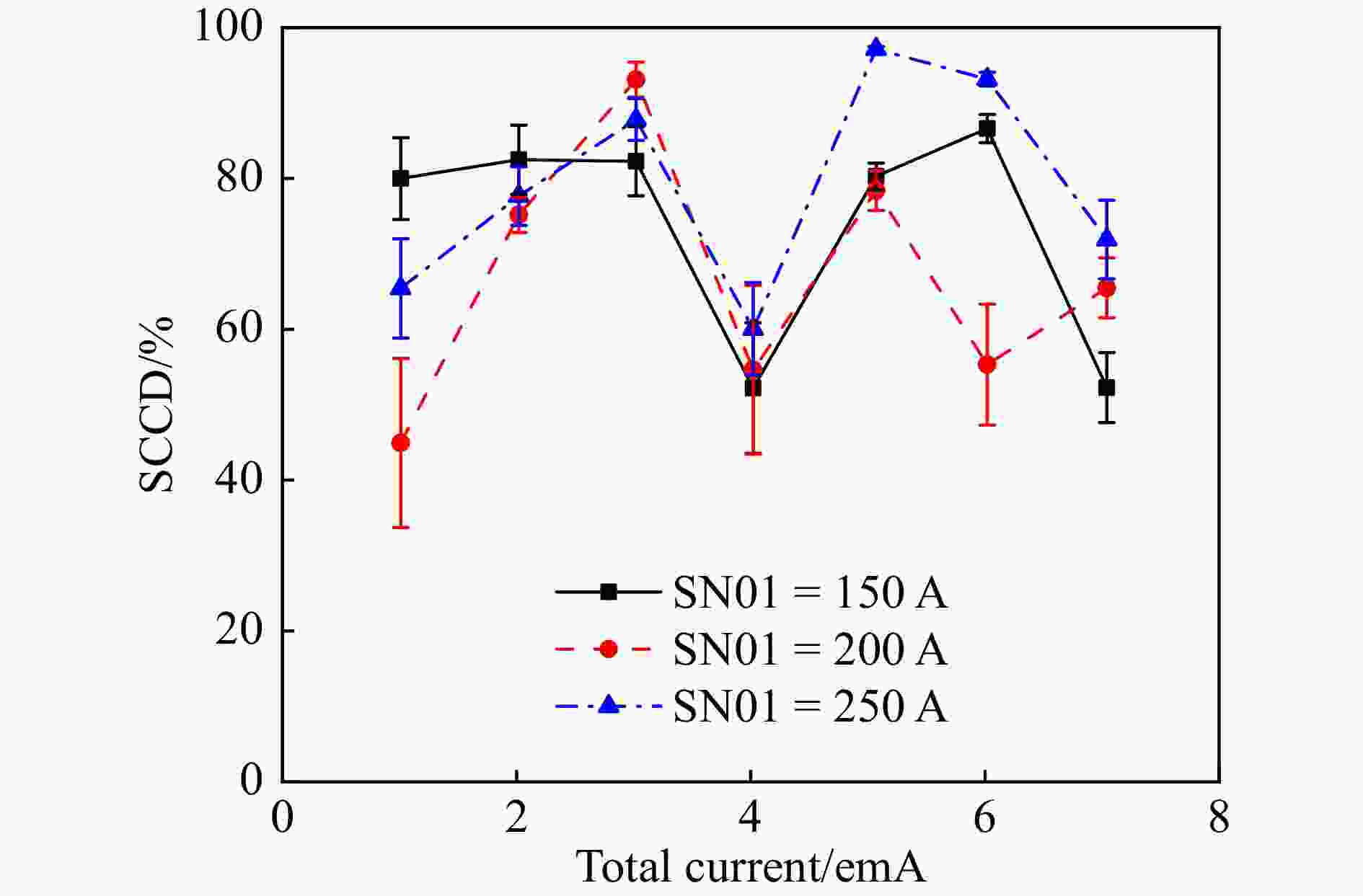
${1} \sim {7}$ emA的混合O离子束SCCD对比如图8所示。可以看出,采用均匀分布模型计算得到的SCCD波动范围较大且规律性较差,而根据实际电流分布模型计算得到的SCCD基本保持在70%左右,且在任意流强下都大于均匀分布模型的SCCD。总流强
${1} \sim {7}$ emA的混合O离子束在SN01分别为150, 200, 250 A时的SCCD对比如图9所示。可以看出,在束流强度不变而束流剖面分布发生变化时,对SCCD的测量值也会产生一些影响,甚至有可能高于束流强度变化对SCCD的影响。 -
通过前期的研究[15],采用实际测量得到的束流剖面模型相对于直接采用束流均匀分布模型能够更准确、更真实地计算出束流的SCCD结果。本研究针对高电荷态强流ECR离子源引出束流离子种类多、空间分布不均匀、对称性差等特点,通过采用较高分辨的束流剖面探测分析装置,结合TEA探测,较为准确地给出了高电荷态ECR源强流离子束引出区的SCCD情况。结果说明,束流剖面的电流分布对剖面的电势分布影响巨大,对SCCD的值也有一定影响。在真空度为1.0×10−5 Pa左右、SN01为150 A时,总流强
${1} \sim {7}$ emA的混合O离子束的SCCD均为70% 左右,这可以作为之后强流混合离子束引出与传输模拟研究的一个参考值。受限于目前的测量手段,我们假定不同电荷态的离子在所测量处的截面分布相同,均等同于束流剖面探测器测得的电流分布,因此混合离子束的速度可以按照束流的电荷态流强分布进行加权平均计算。这种假定会略微影响SCCD测量的精确度,在之后对于更高流强,例如${20} \sim {30}$ emA的混合U离子束的SCCD研究中有待改进。关于更复杂、更高总流强的重离子混合束SCCD的研究工作有待下一步开展。
Space Charge Compensation Study of Low-energy High-intensity Mixed Ion Beams
-
摘要: 空间电荷效应是影响束流传输和束流品质的一个重要因素,特别是对于低能量强流离子束来说。离子束与束流传输线中的剩余气体分子通过电离反应等产生大量二次电子,受离子束的空间电势约束,可以部分补偿空间电荷效应。为了深入研究强流束在低能段的传输,需要准确测量束流的空间电荷补偿度(SCCD),尤其是混合束流的 SCCD。利用一台三栅网式能量分析仪和一台基于128通道皮安表系统构成的束流剖面探测器,分别测量了不同流强和束流分布下的混合O离子束的二次离子能量分布和束流流强分布,从而计算得出SCCD。实验结果表明,在1.0×10−5 Pa的真空度下,不同流强的混合O离子束的SCCD基本在70% 左右;不同束流分布对空间电势分布影响较大,对离子束的SCCD也会有一定程度的影响。Abstract: The space charge effect is one of the key factors affecting ion beam transport and ion beam quality, especially for low-energy high-intensity ion beams. It can be partially compensated by the secondary electrons, which are produced from the ionization of residual gas molecules in the beam pipe and trapped by the space charge potential of ion beams. To study high intensity beam transport in low energy section, it is essential to have an accurate value of space charge compensation degree(SCCD) of the beam, particularly for mixed ion beams. Using a three-grid energy analyzer and a beam profile monitor based on an 128-channel picoammeter system, we measured the secondary ion energy distribution and the beam current distribution of mixed oxygen ion beams of different beam intensities and beam distributions, respectively. Thus the SCCD of the beams can be calculated. The results show that for mixed oxygen ion beams of different intensities, the SCCD are basically around 70% under the vacuum of 1.0×10−5 Pa; The space charge potential of the beams are affected greatly by the beam current distributions, which also consequently have influence on the SCCD of the ion beams.
-
[1] SPÄDTKE P. Review of Scientific Instruments, 2014, 85(2): 02A744. doi: 10.1063/1.4862661 [2] SOLOSHENKO I. Review of scientific instruments, 1996, 67(4): 1646. doi: 10.1063/1.1146909 [3] CHAUVIN N, DELFERRIÈRE O, DUPERRIER R, et al. Review of Scientific Instruments, 2012, 83(2): 02B320. doi: 10.1063/1.3678658 [4] 谭彪, 武启, 杨尧, 等. 原子核物理评论, 2016, 33(1): 36. doi: 10.11804/NuclPhysRev.33.01.036 TAN B, QI W, YANG Y, et al. Nuclear Physics Review, 2016, 33(1): 36. (in Chinese) doi: 10.11804/NuclPhysRev.33.01.036 [5] LU P, PENG S, REN H, et al. Review of Scientific Instruments, 2010, 81(2): 02B711. doi: 10.1063/1.3271257 [6] FERDINAND R, SHERMAN J, STEVENS R R, et al. Spacecharge neutralization Measurement of a 75-keV, 130-mA Hydrogenion Beam[C]//Proceedings of the 1997 Particle Accelerator Conference (Cat. No. 97CH36167), New York: IEEE, 1997: 2723. [7] ULLMANN C, ADONIN A, BEREZOV R, et al. Review of Scientific Instruments, 2016, 87(2): 02B938. doi: 10.1063/1.4939782 [8] WINKLEHNER D, LEITNER D, COLE D, et al. Review of Scientific Instruments, 2014, 85(2): 02A739. doi: 10.1063/1.4854315 [9] LI X, LIU J, YU D, et al. Review of Scientific Instruments, 2019, 90(7): 076107. doi: 10.1063/1.5094090 [10] SUN L, GUO J, LU W, et al. Review of Scientific Instruments, 2016, 87(2): 02A707. doi: 10.1063/1.4933123 [11] ZHAO H, SUN L, ZHANG X, et al. Review of scientific instruments, 2006, 77(3): 03A333. doi: 10.1063/1.2149307 [12] ZHAO H, SUN L, LU W, et al. Review of Scientific Instruments, 2010, 81(2): 02A202. doi: 10.1063/1.3273058 [13] YANG Y, ZHAI Y, JIANG P, et al. Journal of Physics: Conference Series, 2020, 1401: 012019. [14] YU D, LIU J, XUE Y, et al. Review of Scientific Instruments, 2015, 86(11): 115102. doi: 10.1063/1.4934849 [15] SHEN Z, SUN L, JIA Z, et al. Journal of Physics: Conference Series, 2022, 2244: 012090. -




 下载:
下载:




































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号