-
随着新一代放射性束流装置的建设和运行, 远离
$ \beta $ -稳定线区域奇特核的研究已经成为核物理学界最热门的前沿课题之一[1-2]。 在这些原子核中,出现了许多奇特现象,如:晕(皮) [3-4]、能级反转[5-6]、幻数移动[7-8]、奇异放射性[9-10]等。在这些奇特现象中,晕体现了有限量子多体的特殊性质。晕现象的发现改变了人们对核结构的传统认识,开辟了核物理研究的新领域。自从1985 年Tanihata 研究小组在实验上观察到11Li 是双中子晕核以来[11],到目前为止,在实验和理论中观测到了许多晕核,如: 6He [12]、11Be [13-15]、14Be [13, 16]、17B [13, 17]、19B [18]、19C [19-20]、22C [21-22]、29-31F [23-24]、31Ne [25]和37Mg[26]等是中子晕核; 8B [27-28]、 17Ne [29- 30]、17F [31-32]、12B [33]和13B [34]等为质子晕核。更多关于原子核晕结构的实验进展可以阅读文献[3]。这些晕核位于中子或质子滴线附近,它们的费米面是非常接近连续谱,导致价核子很容易被散射到连续谱中。连续谱,尤其是连续谱中的共振态在奇特现象的形成中起着重要的作用[35-36],所以合理地处理连续谱中的单粒子共振态,特别是阈值附近的共振态可以使人们更好地理解原子核的奇特性质。目前,物理学家们发展了许多种理论用于研究连续谱中的单粒子共振态,其中,最主要的是传统散射理论和类束缚态方法。基于散射理论的方法包括
$ R $ -矩阵方法[37-38]、$ K $ -矩阵方法[39]、$ S $ -矩阵方法[40-41]、格林函数方法[42-44]和Jost function [45-46]等。人们为了在计算上更加简单方便以及更有效地处理非束缚问题,发展了一系列的类束缚态方法,它可以像处理束缚态那样去处理共振态,主要包括RSM方法[47]、ACCC方法[48]、CSM方法[49-51]等。这些方法虽然在描述共振态方面取得了成功,但仍存在一些缺陷,特别是难以获得宽共振态。最近,复动量表象(CMR)方法因成功地处理非束缚问题[52]而引起了人们的关注。该方法也被应用到原子和分子系统[53]以及原子核[54-55]的共振研究等不同的领域。鉴于CMR方法可以统一处理束缚态、共振态和连续谱,因此,我们将CMR方法推广到球形相对论框架中[52]研究了单粒子共振态。值得注意的是,这种方法不仅可以应用于窄共振,而且对于宽共振也非常有效[52, 56-66]。由于相对论点耦合(RMFPC)模型非常成功地描述了各种核现象[67],Wang等[68]发展了RMFPC-CMR方法,以Sn同位素为例,系统地计算了单粒子共振态的能量和宽度。随后,我们利用Bardeen-Cooper-Schripffcr(BCS)近似处理了束缚态和共振态之间的耦合[69-71],发展了RMFPC-CMR-BCS方法[72],我们用该方法研究了Ce同位素的基态性质,发现在Ce同位素中子滴线附近的核中出现了晕和巨晕现象。
目前,在实验和理论方面对晕核的研究主要集中在轻核区域,当然,一些理论也在重核区域预测到可能存在晕或巨晕现象。但是,对于中等质量核中是否存在晕现象,目前的研究还是相对较少。在文献[73]中,人们利用核密度泛函理论系统地研究了中等质量核中的奇特结构,并预测到在Cr和Sn同位素的中子滴线附近存在晕现象。接着,在文献[62]中,我们通过基于简单Woods-Saxon势的复动量表象方法研究了比37Mg重的奇特核,并得到75Cr、77Fe和53Ar可能是中子晕核的结论。近年来,Horiuchi等[74]在Cr同位素中发现了集体晕现象。
$ Z = 20 $ 到$ Z = 28 $ 区域是一个研究核结构演化很有趣的区域。在这一区域,出现了许多奇特现象,如幻数的变化、中子晕(皮)等。因此,对本区域奇特原子核同位素链的系统研究有助于我们更好地理解核结构。考虑到最近发展的RMFPC-CMR-BCS方法在研究奇特核结构以及单粒子共振态方面的优越性,本文将利用该方法[72]研究丰中子Cr同位素的奇特结构并预测新的奇特现象。在第2部分,概述了RMFPC-CMR-BCS方法的理论框架;在第3部分,介绍了RMFPC-CMR-BCS方法研究原子核奇特结构的一些主要结果;最后,第4部分给出小结。 -
在研究丰中子Cr 同位素的奇特结构之前,先简要介绍一下RMFPC-CMR-BCS的理论框架[68,72]。点耦合顶点的基本模块是一般类型的两费米子项
$(\bar \psi {o_\tau }\varGamma \psi ), {o_\tau } \in \{ 1,{\tau _i}\} ,\;\varGamma \in \{ 1,{\gamma _\mu },{\gamma _5},{\gamma _5}{\gamma _\mu },{\sigma _{\mu v}}\}$ ,其中,$ \psi $ 为核子的Dirac旋量场,$ {\tau _i} $ 是同位旋泡利矩阵,$\varGamma$ 为4×4的Dirac矩阵之一。RMFPC理论是从拉格朗日密度出发$$ L = {L^{{\text{free}}}} + {L^{{\text{4f}}}} + {L^{{\text{em}}}} + {L^{{\text{der}}}} + {L^{{\text{hot}}}}, $$ (1) 其中:
$ {L^{{\text{free}}}} $ 、$ {L^{{\text{4f}}}} $ 、$ {L^{{\text{em}}}} $ 、$ {L^{{\text{der}}}} $ 和$ {L^{{\text{hot}}}} $ 分别为自由核子项、四费米子点耦合项、质子之间电磁相互作用项、密度和流微商项以及高阶耦合项的拉氏量密度,具体如下:$$ {L^{{\text{free}}}} = \bar \psi ({\rm{i}}{\gamma _\mu }{\partial ^\mu } - m)\psi , $$ $$ \begin{split} {L^{{\text{4f}}}} =& - \frac{1}{2}{\alpha^{} _S}{(\bar \psi \psi )^2} - \frac{1}{2}{\alpha ^{}_V}(\bar \psi {\gamma _\mu }\psi )(\bar \psi {\gamma ^\mu }\psi ) - \\& \frac{1}{2}{\alpha^{} _{{TS} }}(\bar \psi {\tau }\psi )(\bar \psi {\tau }\psi ) - \frac{1}{2}{\alpha^{} _{TV}}(\bar \psi {\tau }{\gamma^{} _\mu }\psi )(\bar \psi {\tau }{\gamma ^\mu }\psi ), \end{split} $$ $$ {L^{{\text{em}}}} = - \frac{1}{4}\big[{F^{\mu v}}{F_{\mu v}} + 2e(1 - {\tau _3})(\bar \psi {\gamma ^\mu }\psi ){A_\mu }\big], $$ $$ \begin{split} {L^{{\text{der}}}} =& - \frac{1}{2}{\delta _S}{\partial _v}(\bar \psi \psi ){\partial ^v}(\bar \psi \psi ) - \frac{1}{2}{\delta _{\text{V}}}{\partial _v}(\bar \psi {\gamma _\mu }{\psi} ){\partial ^v}(\bar \psi {\gamma ^\mu }\psi ) - \\& \frac{1}{2}{\delta _{{TS} }}{\partial _v}(\bar \psi {{{{\boldsymbol{\tau}}}} }\psi ){\partial ^v}(\bar \psi {{\boldsymbol{\tau}} }\psi ) - \frac{1}{2}{\delta _{{TV} }}{\partial _v}(\bar \psi {{\boldsymbol{\tau}} }{\gamma _\mu }\psi ){\partial ^v}(\bar \psi {{\boldsymbol{\tau}} }{\gamma ^\mu }\psi ), \end{split}$$ $$ {L^{{\text{hot}}}} = - \frac{1}{3}{\beta _S}{(\bar \psi \psi )^3} - \frac{1}{4}{\gamma _S}{(\bar \psi \psi )^4} - \frac{1}{4}{\gamma _V}{\big[(\bar \psi {\gamma _\mu }\psi )(\bar \psi {\gamma ^\mu }\psi )\big]^2}, $$ 式(1)所有符号的含义与文献[67]中相同。由拉格朗日密度出发,经过一系列的计算可以得到核子的狄拉克方程
$$ \big[ {{{{\boldsymbol{\alpha}} }} \boldsymbol\cdot {{{\boldsymbol{p}}}} + \beta (m + S) + V} \big]\psi = \varepsilon \psi , $$ (2) 这里,
$S(r) = {{\varSigma} _s}$ 和$V(r) = {{\varSigma} ^\mu } + {\boldsymbol{\tau }} \boldsymbol\cdot {\boldsymbol\varSigma} _{Tv}^\mu$ 分别为标量势和矢量势,$$ \left\{ \begin{gathered} {\varSigma}_s = {\alpha^{} _s}{\rho^{} _s} + {\beta ^{}_s}\rho _s^2 + {\gamma^{} _s}\rho _s^3 + {\delta^{} _s}\vartriangle {\rho^{} _s} \\ {\varSigma}^\mu = {\alpha ^{}_v}j_v^\mu + {\gamma ^{}_v}{(j_v^\mu )^3} + {\delta ^{}_v}\vartriangle j_v^\mu + e{A^\mu } \\ {\boldsymbol\varSigma} _{Tv}^\mu = {\alpha ^{}_{Tv}}\boldsymbol j_{Tv}^\mu + {\delta^{} _{Tv}}\vartriangle \boldsymbol j_{Tv}^\mu \\ \end{gathered} \right. , $$ (3) 其中:
${{\varSigma} _s}$ 是同位旋标量-标量自能;${{\varSigma} ^\mu }$ 是同位旋标量-矢量自能;${\boldsymbol{\varSigma}} _{Tv}^\mu$ 是同位旋矢量-矢量自能。方程(2)中束缚态的解可以用常规的方法得到。为了得到物理共振态的非束缚解,我们将式(2)转化到动量表象下$$ \int {{\rm d}{{\boldsymbol{k}}^{'}}\left\langle {{\boldsymbol{k}}\left| H \right|{{\boldsymbol{k}}^{'}}} \right\rangle } \psi \left( {{{\boldsymbol{k}}^{'}}} \right) = \varepsilon \psi \left( {\boldsymbol{k}} \right)。 $$ (4) 这里,
$H = {\boldsymbol{\alpha }} \boldsymbol\cdot {\boldsymbol{p}} + \beta (m + S) + V$ ,$\psi \left( {\boldsymbol k} \right)$ 和$ \varepsilon $ 分别为动量波函数和单粒子能量。为了求解方程(4),波函数可以用分离变量法得到$$ \psi ({\boldsymbol{k}}) = \left( {\begin{array}{*{20}{c}} {f(k){\phi _{lj{m_j}}}({\Omega _k})} \\ {g(k){\phi _{\tilde lj{m_j}}}({\Omega _k})} \end{array}} \right)。 $$ (5) 其中:
$ f\left( k \right) $ 是关于l和j的径向分量;${\phi _{lj{m_j}}}\left( {{\Omega _k}} \right) = \sum\limits_{{m_s}} {\left\langle {{{\rm lm}\frac{1}{2}{m_s}}} \mathrel{\left | {\vphantom {{lm\frac{1}{2}{m_s}} {j\Omega }}} \right. } {{j\Omega }} \right\rangle } {Y_{lm}}\left( {{\Omega _k}} \right){\chi _{{m_s}}}$ 是角向部分;$ {Y_{lm}}\left( {{\Omega _k}} \right) $ 和$ {\chi _{{m_s}}} $ 分别是球谐函数和自旋波函数。将式(5)带入到式(4)中进行一系列的计算,式(4)的Dirac方程可以写成$$ \begin{gathered} mf(k) - kg(k) + \int {k{'^2}} {{\rm{d}}}k'{V_ + }(k,k')f(k') = \varepsilon f(k), \\ - kf(k) - mg(k) + \int {k{'^2}} {{\rm{d}}}k'{V_ - }(k,k')g(k') = \varepsilon g(k)。 \\ \end{gathered} $$ (6) 这里
$$ \begin{gathered} {V_ + }(k,k') = \frac{2}{\pi }\int {{r^2}{{\rm{d}}}r\left[ {V(r) + S(r)} \right]{j_l}} (k'r){j_l}(kr), \\ {V_ - }(k,k') = \frac{2}{\pi }\int {{r^2}{{\rm{d}}}r\left[ {V(r) - S(r)} \right]{j_{\tilde l}}} (k'r){j_{\tilde l}}(kr)。 \\ \end{gathered} $$ (7) 在复动量空间中求解式(6),不仅可以得到束缚态,而且也可以得到共振态,在束缚态和共振态的基础上,用BCS近似处理对关联,推导细节见文献[68, 72]。
-
基于上述理论公式,我们用RMFPC-CMR-BCS方法研究了丰中子Cr同位素的奇特结构。在本文中,所有束缚态和物理共振态之间的耦合用BCS近似来处理。为方便起见,中子和质子的对力强度参数[75]采用经验公式
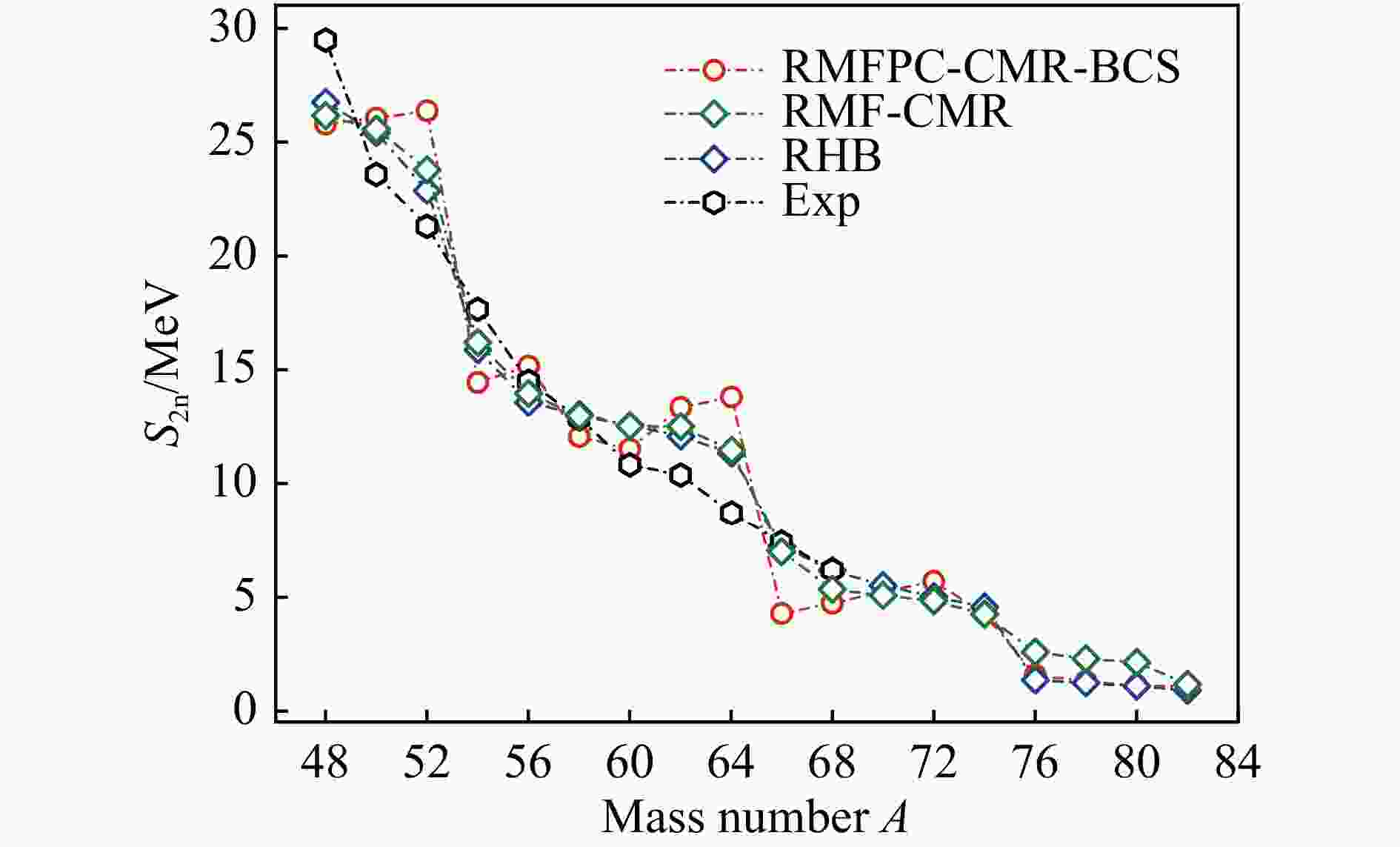
$ \Delta = \delta /\sqrt A $ ($ \delta $ 和A分别为能隙参数和核子的质量,本文采用的能隙参数为$\delta = 12$ )得到。对于RMFPC理论,采用有效相互作用PC-PK1 [67]。本文所涉及的中子数是从$N = 24$ 到$N = 58$ ,这是因为奇特现象主要出现在极丰中子核中。采用的数值细节与文献[52, 68, 72]相同。在图1中,我们展示了Cr同位素的双中子分离能
${S_{\rm{2n}}}$ ,并与可用的实验数据[76]以及Relativistic Hartree-Bogoliubov(RHB)和RMFPC-CMR的计算结果进行了比较。可以看到RMFPC-CMR-BCS的结果与实验结果有3~5 MeV的偏差,这可能是高估了配对效应,但这并不影响我们对Cr同位素中晕现象的探索。除主壳隙外,${S_{\rm{2n}}}$ 随中子数N 的变化一般是单调递减,当${S_{\rm{2n}}}$ 显著下降并出现强烈的不连续时则表明出现中子壳闭。我们可以看到在52Cr和64Cr处出现了强烈的不连续,这意味着传统幻数$N = 28$ 和$N = 40$ 存在。同时,在74Cr处也出现了不连续,这验证了传统幻数$N = 50$ 。此外,我们也可以看到Cr同位素的双中子分离能${S_{\rm {2n}}}$ 在极丰中子一侧是非常接近于零,也就是说,这些核是非常弱束缚的,这支持中子晕(皮)的形成。核半径是描述原子核性质的另一个重要物理量。在图2中,我们得到了Cr同位素的中子、质子和电荷均方根(rms)半径。为了便于比较,这里也列出了RMFPC-CMR和RHB方法对中子和质子rms半径的计算结果和已有电荷半径的实验数据[77]。可以看出,这三种方法计算得到的中子和质子的rms半径随质量数
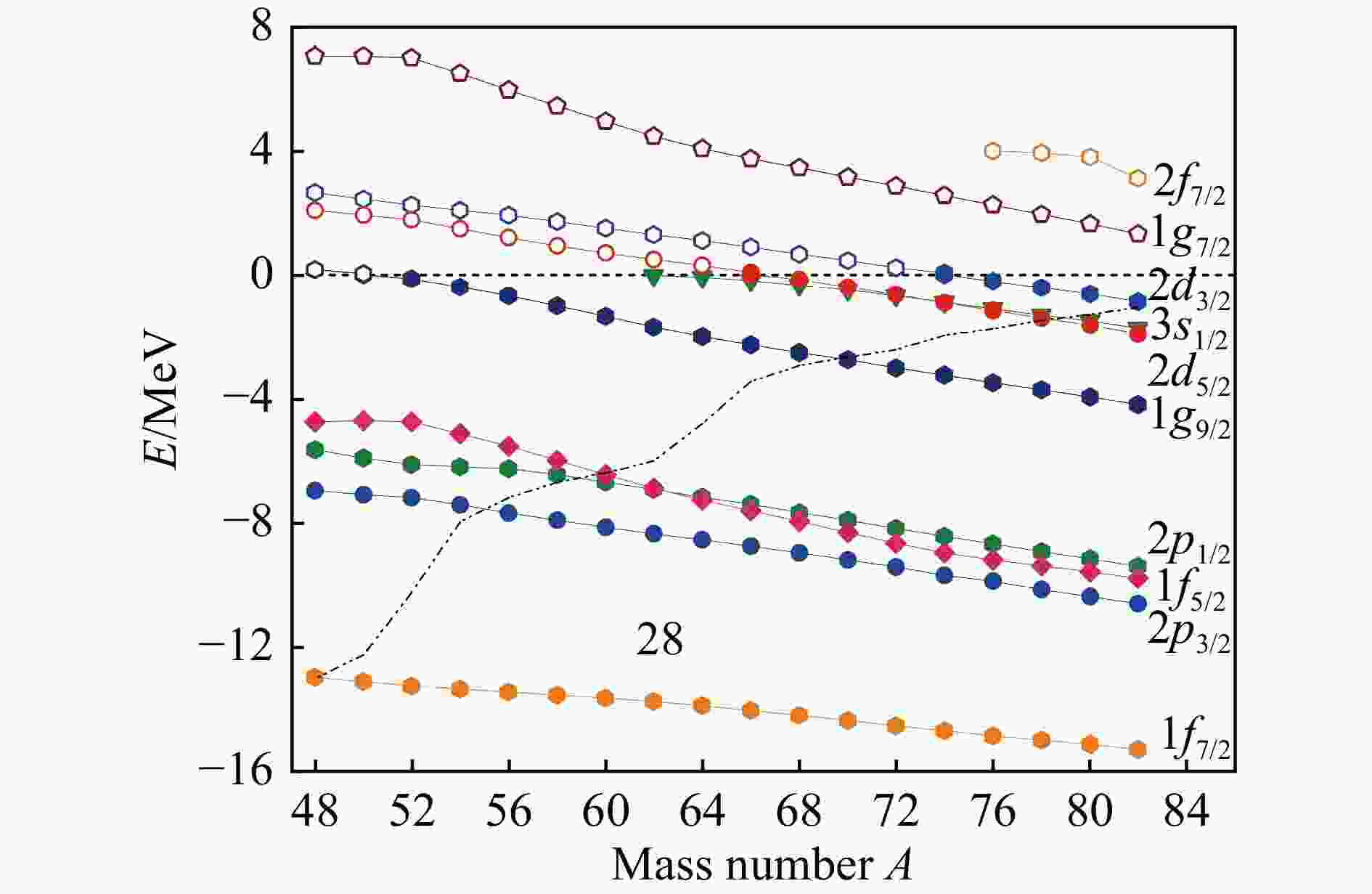
$ A $ 的变化趋势是相似的。同时,可以看到RMFPC-CMR-BCS方法计算得到的电荷半径略小于实验值,但是,从图2中我们可以发现计算得到的电荷半径和已有实验数据随质量数A的变化趋势是相似的。这表明我们的计算结果是可靠的。随着质量数A的增加,所考虑同位素的中子rms半径和质子rms半径均增加。我们可以看到,中子均方根半径增加的斜率是大于质子的斜率。对于质子均方根半径,这三种计算结果几乎相同。对于中子rms半径, RMFPC-CMR-BCS的计算结果略大于RMFPC-CMR和RHB 的计算结果,这可能是高估了配对效应。在$N > 50$ 时,中子rms半径急剧增大,这意味着76−82Cr中可能存在晕结构。在这里,我们研究了Cr同位素链末端且靠近中子滴线的原子核,对于这些核,中子的均方根半径由于中子的空间弥散而显著增加,这意味着在中子滴线附近存在厚中子皮或中子晕。为了更好地理解丰中子Cr 同位素的奇特结构,在图3中,展示了所考虑同位素的单粒子能量。在这里,束缚态和共振态分别用实心和空心图案标记。费米面用短虚线标记。我们可以看到能级
$ 1{f_{7/2}} $ 和$ 2{p_{3/2}} $ 、$ 2{p_{1/2}} $ 和$ 1{g_{9/2}} $ 之间分别有很大的能隙,这意味着传统幻数$N = 28$ 和$N = 40$ 存在。同时,能级$ 1{g_{9/2}} $ 和$ 2{d_{5/2}} $ 之间也存在较大的能隙,这验证了传统幻数$N = 50$ 。此外,对于所考虑的Cr 同位素,能级$ 1{g_{7/2}} $ 始终保持共振态,而能级$ 2{d_{5/2}} $ 和$ 2{d_{3/2}} $ 随着质量数的增加由共振态变为弱束缚态。在$A \geqslant 62$ 时,弱束缚能级$ 3{s_{1/2}} $ 出现,在极丰中子一侧非常接近$ 2{d_{5/2}} $ 能级。随着质量数的增加,能级$ 3{s_{1/2}} $ 、$ 2{d_{5/2}} $ 和$ 2{d_{3/2}} $ 非常接近于零势能面,它们的占据有利于中子晕的形成。虽然上述结果支持在极丰中子Cr同位素中出现中子晕现象,但为了进一步证实从单粒子能级得到的结果,我们需要知道单粒子能级的占据情况,从而揭示晕形成的物理机制。图4展示了64−82Cr 单粒子能级的占据几率。在本文中,为了更加清楚地看到单粒子的占据情况,我们仅给出了在图3中展示的束缚态和共振态的占据几率。化学势的位置用垂直虚线表示。由于64Cr是一个中子数为
$N = 40$ 的幻数核,其能级$ 2{p_{1/2}} $ 的占据是饱和的,因此我们不需要考虑对关联对该核的贡献。从$N = 42$ 开始,价中子开始占据$N = 40$ 以上的能级$ 1{g_{9/2}} $ ,在74Cr时,其占据几率达到0.9以上,几乎接近饱和。随着质量数进一步增加,我们可以看到弱束缚能级$ 2{d_{5/2}} $ 、$ 2{d_{3/2}} $ 和$ 3{s_{1/2}} $ 的占据几率越来越显著。从76Cr到82Cr,能级$ 2d $ 和$ 3s $ 的占据支持了在丰中子Cr 同位素中存在晕结构。晕核的密度尾部在空间上有一定的弥散。在图5,我们展示了从74Cr到82Cr的质子和中子的密度分布。可以看到,随着半径r的增加,总质子密度迅速下降,减小到零,而中子密度相对于质子密度在空间中更加弥散。这种密度分布上的差异提醒我们,在中子滴线附近的原子核中存在较大的中子晕。我们可以看到在74Cr 时,中子密度随
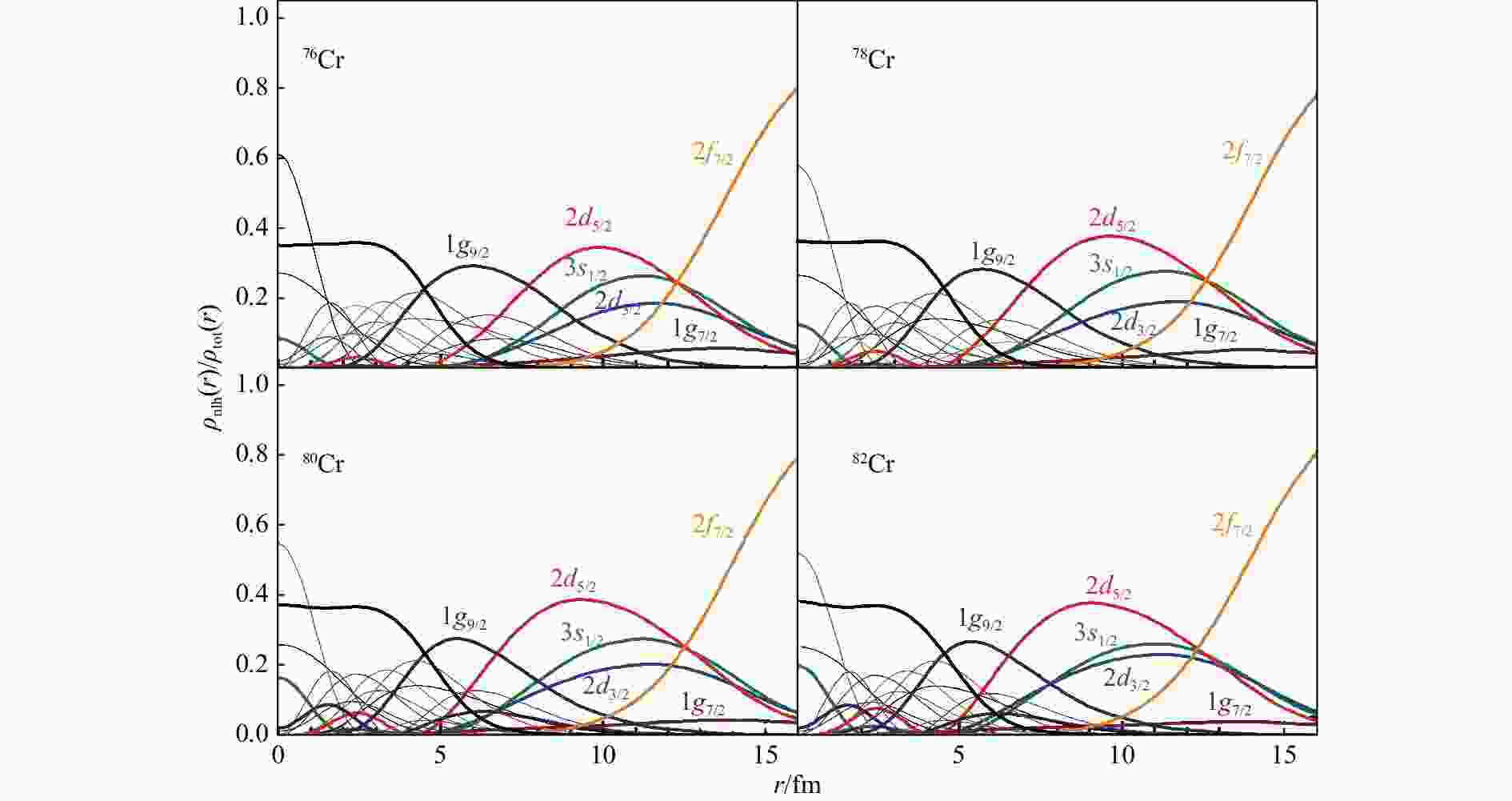
$ r $ 的增加迅速减小到零,然而,76Cr到82Cr对应的中子密度分布在空间上变得更加弥散,它们的尾部都拖着一条长长的尾巴,这意味着76−82Cr 对应的原子核是中子晕核。为了进一步证明上面所得到的结果以及弄清楚这些单粒子轨道是否对弥散密度分布有贡献,我们给出了极丰中子核76−82Cr的不同单粒子能级对总中子密度的贡献。在图6 中,4个子图分别展示了76Cr、78Cr、80Cr和82Cr的单中子能级密度与总中子密度之比(为方便起见,以下简称密度比)。从
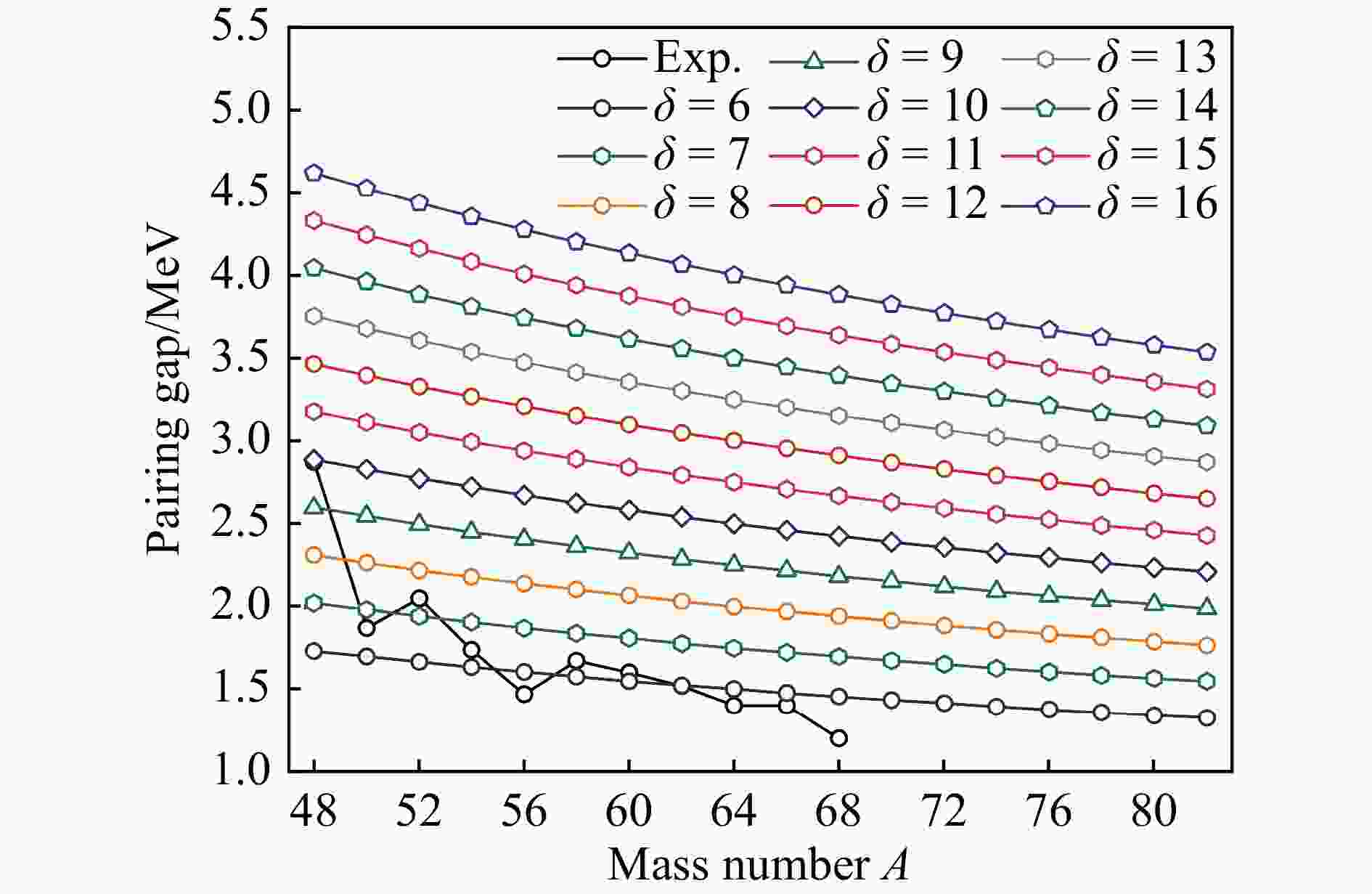
$r = 8$ fm到$r = 11$ fm,弱束缚能级$ 2{d_{5/2}} $ 、$ 2{d_{3/2}} $ 和$ 3{s_{1/2}} $ 的密度比相对较大。随着半径$ r $ 的进一步增大,弱束缚能级$ 2{d_{5/2}} $ 、$ 2{d_{3/2}} $ 和$ 3{s_{1/2}} $ 的密度比逐渐衰减到零,并可以看到能级$ 2{d_{5/2}} $ 的衰减速度快于能级$ 2{d_{3/2}} $ 和$ 3{s_{1/2}} $ 。当$r > 13$ fm 时,总中子的密度分布主要来自共振态$ 2{f_{7/2}} $ 和$ 1{g_{7/2}} $ 的贡献。但由于这两个能级的占据几率很小以及离心势垒较大,导致它们的绝对密度分布很小。因此,在76−82Cr 中,中子密度分布长长的尾巴主要来自弱束缚能级$ 2{d_{3/2}} $ 和$ 3{s_{1/2}} $ 的贡献,它们在晕结构中起着至关重要的作用。虽然高-$ l $ 态对弥散密度分布的贡献相对较小,但是在晕轨道附近,高-$ l $ 态的存在是特别重要的,因为它们在费米面附近产生了相当大的能级密度,并显著增强了配对效应来稳定晕同位素。最后,为了进一步探索在图1和图2中RMFPC-CMR-BCS的计算结果较大于实验值的原因,在图7展示了对能隙随能隙参数
$ \delta $ 的演化,并与可用的实验数据[76]进行了对比。我们可以看到,$ \delta $ 从6到16,对能隙随着质量数的增加而单调递减。在48Cr时,$\delta = 8$ 得到的对能隙和实验数据符合得很好。接着,从50Cr到52Cr,可以看到$\delta = 7$ 得到的对能隙和实验数据符合得较好。随着中子数的进一步增加,从54Cr到56Cr,能隙参数$\delta = 6$ 得到的对能隙和实验数据符合得较好。然而,在68Cr时,用$\delta = 6$ 计算得到的对能隙和实验值出现了一定的偏差,这说明,不同核子的对能隙对$ \delta $ 有较大的依赖。并且,我们也计算了在82Cr时中子单粒子能量随能隙参数$ \delta $ 的演化。发现弱束缚能级$ 3{s_{1/2}} $ 和$ 2{d_{3/2}} $ 以及共振能级$ 1{g_{7/2}} $ 和$2 f_{7 / 2} $ 随着$ \delta $ 的增加而缓慢下降,特别是对晕现象有重要贡献的弱束缚能级$ 3{s_{1/2}} $ 和$ 2{d_{3/2}} $ 随着$ \delta $ 的增加几乎没有变化。为了节省页面,在本文中就没有展示在82Cr时中子单粒子能量随$ \delta $ 的变化关系图。虽然在计算中高估了对效应,但这对我们的结果并没有影响,因此,能隙参数$\delta = 12$ 选取也是合理的。在后续的工作中我们会对这个因素进行深入的讨论和研究。 -
本文用RMFPC-CMR-BCS方法研究了Cr同位素的奇特结构。将计算得到的双中子分离能数据与RMFPC-CMR和RHB方法的计算结果以及现有的实验数据进行了对比,并验证了传统幻数
$N = 28$ 、$N = 40$ 和$N = 50$ 。同时,对于极丰中子一侧的原子核,它们的$ {S_{{2n}}} $ 非常接近于零以及在$ N > 50$ 时中子rms半径急剧增大,这意味着在76−82Cr中可能存在晕结构。随后本文从获得的单粒子能级发现,当价中子占据弱束缚能级$ 3{s_{1/2}} $ 和$ 2d $ 时,有利于中子晕的形成。接着,本文计算了价核子在费米面附近能级上的占据几率,并得到了质量数从$A = 74$ 到$A = 82$ 的中子密度分布,我们发现A=76~82对应的原子核是中子晕核。为了进一步弄清单粒子能级对弥散密度分布的贡献,我们还计算了每个单中子能级密度与总中子密度之比。我们发现几个低角动量弱束缚能级对弥散密度分布有显著的贡献。结果表明,76−82Cr总中子密度尾部拖着一条长长的尾巴主要来自于$ 3{s_{1/2}} $ 和$ 2{d_{3/2}} $ 能级的贡献,它们在晕现象的形成中有显著的作用。本文对丰中子Cr同位素奇特结构的预测将为探索其他中子滴线核的基态性质提供一定的基础,同时,对Cr同位素奇特结构的研究也为下一阶段研究$Z = 20$ 附近其他原子核的基态性质提供了坚实的理论基础。下一步,为了解决对能隙等结果对能隙参数的依赖性以及为了很好地描述丰中子奇特核中的基态性质,接下来,我们将采用Bogoliubov变换来处理对关联,发展描述球形核的RMF-CMR-Bogliubov理论,探索
$Z = 20$ 附近其他丰中子核的壳层结构,弄清束缚态和共振态在奇特结构中所扮演的角色,揭示奇特现象形成的物理机制,相关研究工作正在计算分析当中。
Study on the Exotic Structures of the Neutron-rich Cr Isotopes by the Complex Momentum Representation Method
-
摘要: 奇特核的研究是核物理中最有趣的前沿课题之一。中等质量核中是否存在晕现象,目前的研究相对较少。复动量表象(CMR)方法可以用来探索原子核中的奇特结构。连续谱阈值附近的共振态在奇特现象的形成中起着重要的作用。利用相对论点耦合框架下的复动量表象(RMFPC-CMR)方法研究了丰中子Cr 同位素中的奇特结构,得到的非常接近于零的双中子分离能和迅速增大的中子均方根半径表明在靠近中子滴线的Cr 同位素中存在晕结构。从获得的单粒子能级、费米面附近价核子占据几率、中子和质子密度分布以及各能级对原子核密度的贡献可以发现
$ 3{s_{1/2}} $ 和$ 2{d_{3/2}} $ 能级的占据有利于中子晕的形成。研究发现,低角动量弱束缚能级对异常增大的半径和弥散密度分布有显著的贡献,这导致靠近中子滴线的76-82Cr 是中子晕核。这一预测结果对在实验中探索中等质量区的晕核具有一定的参考价值。Abstract: The study of exotic nuclei is one of the most interesting frontier topics in nuclear physics. There are relatively few studies on the existence of halo in medium-mass nuclei. The complex momentum representation(CMR) method can be used to explore exotic structures in nuclei. The resonant states near the continuum threshold play an important role in the formation of exotic phenomena. Therefore, the relativistic point coupled and the complex momentum representation (RMFPC-CMR) method is used to explore the exotic structures for the neutron-rich Cr isotopes. The two-neutron separation energies have been calculated to be very close to zero, and the mean square (rms) radii of neutron also have increased sharply, implying the presence of halo structures in the Cr isotopes near the neutron drip line. The single-particle levels, the occupation probabilities of valence nucleons on the levels near the Fermi surface, the neutron and proton density distributions, and the contribution of every level to the nucleus density are obtained, it can be found that the occupations of the levels$ 3{s_{1/2}} $ and$ 2{d_{3/2}} $ are beneficial to the formation of neutron halo. It is found that the unusual increases of rms radii and diffuse distributions of neutron densities come mainly from the contributions of the weakly bound levels with lower orbital angular momentum, which leads to the neutron halos of 76-82Cr near the neutron drip line. This prediction has a certain reference value for exploring the halo nuclei in the medium mass region in experiments. -
-
[1] TANIHATA I. J Phys G:Nucl Part Phys, 1996, 22: 157. doi: 10.1088/0954-3899/22/2/004 [2] OZAWA A, KOBAYASHI T, SUZUKI T, et al. Phys Rev Lett, 2000, 84(24): 5493. doi: 10.1103/PhysRevLett.84.5493 [3] TANIHATA I, SAVAJOLS H, KANUNGO R. Prog Part Nucl Phys, 2013, 68: 215. doi: 10.1016/j.ppnp.2012.07.001 [4] NNAKMURA T, SAKURAI H, WATANABE H. Prog Part Nucl Phys, 2017, 97: 53. doi: 10.1016/j.ppnp.2017.05.001 [5] WILSON G L, CATFORD W N, ORR N A, et al. Phys Lett B, 2016, 759(10): 417. doi: 10.1016/j.physletb.2016.05.093 [6] LONGFELLOW B, WEISSHAAR D, GADE A, et al. Phys Rev Lett, 2020, 125(23): 232501. doi: 10.1103/physrevlett.125.232501 [7] GARCIA RUIZ R F, BISSELL M L, BLAUM K, et al. Nat Phys, 2016, 12(6): 594. doi: 10.1038/nphys3645 [8] LEISTENSCHNEIDER E, DUNLING E, BOLLEN G, et al. Phys Rev Lett, 2021, 126(4): 042501. doi: 10.1103/PhysRevLett.126.042501 [9] OLSEN E, PFÜTZNER M, BIRGR N, et al. Phys Rev Lett, 2013, 110: 222501. doi: 10.1103/PhysRevLett.111.139903 [10] MA Y G, FANG D Q, SUN X Y, et al. Phys Lett B, 2015, 743(9): 306. doi: 10.1016/j.physletb.2015.02.066 [11] TANIHATA I, HAMAGAKI H, HASHIMOTO O, et al. Phys Lett B, 1985, 160(6): 380. doi: 10.1016/0370-2693(85)90005-X [12] ZHUKOV M V, DANILIN B V, FEDOROV D V, et al. Phys Rep, 1993, 231(4): 151. doi: 10.1016/0370-1573(93)90141-Y [13] TANIHATA I, KOBAYASHI T, YAMAKAWA O, et al. Phys Lett B, 1985, 206(4): 592. doi: 10.1016/0370-2693(88)90702-2 [14] FUKUDA M, ICHIHARA T, INABE N, et al. Phys Lett B, 1991, 268(3-4): 339. doi: 10.1016/0370-2693(91)91587-L [15] ZAHAR M, BELBOT M, KOLATA J J, et al. Phys Rev C, 1993, 48(4): R1484(R). doi: 10.1103/PhysRevC.48.R1484 [16] THOMPSON I J, ZHUKOV M V. Phys Rev C, 1996, 53(2): 708. doi: 10.1103/PhysRevC.53.708 [17] YANG Z H, KUBOTA Y, ORSI A, et al. Phys Rev Lett, 2021, 126(8): 082501. doi: 10.1103/PhysRevLett.126.082501 [18] COOK K J, NAKAMURA T, KONDO Y, et al. Phys Rev Lett, 2020, 124(21): 212503. doi: 10.1103/PhysRevLett.124.212503 [19] BAZIN D, BROWN B A, BROWWN J, et al. Phys Rev Lett, 1995, 74(18): 3569. doi: 10.1103/PhysRevLett.74.3569 [20] KANUNGO R, TANIHATA I, OGAWA Y, et al. Nucl Phys A, 2002, 701(1-4): 378. doi: 10.1016/S0375-9474(01)01614-1 [21] TANAKA K, YAMAGUCHI T, SUZUKI T, et al. Phys Rev Lett, 2010, 104(6): 062701. doi: 10.1103/PhysRevLett.104.062701 [22] SUN X X, ZHAO J, ZHOU S G. Phys Lett B, 2018, 785(10): 530. doi: 10.1016/j.physletb.2018.08.071 [23] BAGCHI S, KANUNGO R, TANAKA Y K, et al. Phys Rev Lett, 2020, 124(22): 222504. doi: 10.1103/PhysRevLett.124.222504 [24] MICHEL N, LI J G, XU F R, et al. Phys Rev C, 2020, 101(3): 031301(R). doi: 10.1103/PhysRevC.101.031301 [25] NAKAMURA T, KOBAYASHI N, KONDO Y, et al. Phys Rev Lett, 2009, 103(26): 262501. doi: 10.1103/PhysRevLett.103.262501 [26] KOBAYASHI N, NAKAMURA T, KONDO Y, et al. Phys Rev Lett, 2014, 112(24): 242501. doi: 10.1103/PhysRevLett.112.242501 [27] WARNER R E, KELLEY J H, ZECHER P, et al. Phys Rev C, 1995, 52(3): R1166(R). doi: 10.1103/PhysRevC.52.R1166 [28] NEGOITA F, BORCER C, CARSTOIU F, et al. Phys Rev C, 1996, 54(4): 1787. doi: 10.1103/PhysRevC.54.1787 [29] KANUNGO R, CHIBA M, ADHIKARI S, et al. Phys Lett B, 2003, 571(1-2): 21. doi: 10.1016/j.physletb.2003.07.050 [30] JEPPESEN H, KANUNGO R, ANU-IBRAHIM B, et al. Nucl Phys A, 2004, 739(1-2): 57. doi: 10.1016/j.nuclphysa.2004.03.145 [31] MORLOCK R, KUNZ R, MAYER A, et al. Phys Rev Lett, 1997, 79(20): 3837. doi: 10.1103/PhysRevLett.79.3837 [32] REN Z Z, FAESSLER A, BOBY A. Phys Rev C, 1998, 57(5): 2752. doi: 10.1103/PhysRevC.57.2752 [33] LIN C J, LIU Z H, ZHANG H Q, et al. Chin Phys Lett, 2001, 18(9): 1183. doi: 10.1088/0256-307X/18/9/309 [34] LIU Z H, LIN C J, ZHANG H Q, et al. Phys Rev C, 2001, 64(3): 034312. doi: 10.1103/PhysRevC.64.034312 [35] MENG J, ZHOU S G. J Phy. G: Nucl Part Phys, 2015, 42(9): 093101. doi: 10.1088/0954-3899/42/9/093101 [36] ZHOU S G. Phys Scr, 2016, 91(6): 063008. doi: 10.1088/0031-8949/91/6/063008 [37] WIGNER E P, EISENBUD L. Phys Rev, 1947, 72(1): 29. doi: 10.1103/PhysRev.72.29 [38] HALE G M, BROWN R E, JARMIE N. Phys Rev Lett, 1987, 59(7): 763. doi: 10.1103/PhysRevLett.59.763 [39] HUMBLET J, FILIPPONE B W, KOONIN S E. Phys Rev C, 1991, 44(6): 2530. doi: 10.1103/PhysRevC.44.2530 [40] TAYLOR J R. Scattering Theory: The Quantum Theory on Nonrelativistic Collisions[M]. New York: John Wiley and Sons, 1972. [41] CAO L G, MA Z Y. Phys Rev C, 2002, 66(2): 024311. doi: 10.1103/PhysRevC.66.024311 [42] ECONOMOU E N. Green’s Function in Quantum Physics[M]. Berlin: Springer-Verlag, 2006. [43] ZHANG Y, MATSUO M, MENG J. Phys Rev C, 2012, 86(5): 054318. doi: 10.1103/PhysRevC.86.054318 [44] SUN T T, ZHANG S Q, ZHANG Y, et al. Phys Rev C, 2014, 90(5): 054321. doi: 10.1103/PhysRevC.90.054321 [45] LU B N, ZHAO E G, ZHOU S G. Phys Rev Lett, 2012, 109(7): 072501. doi: 10.1103/PhysRevLett.109.072501 [46] LU B N, ZHAO E G, ZHOU S G. Phys Rev C, 2013, 88(2): 024323. doi: 10.1103/PhysRevC.88.024323 [47] HAZI A U, TAYLOR H S. Phys Rev A, 1970, 1(4): 1109. doi: 10.1103/PhysRevA.1.1109 [48] KUKULIN V I, KRASNOPLŚKY V M, HORÁCEK J. Theory of Resonances: Principles and Applications[M]. Dordrecht: Kluwer, 1989. [49] AGUILAR J, COMBES J M. Commun Math Phys, 1971, 22(4): 269. doi: 10.1007/bf01877510 [50] BALSLEV E, COMBES J M. Commun Math Phys, 1971, 22(4): 280. doi: 10.1007/bf01877511 [51] SIMON B. Commun Math Phys, 1972, 27(1): 1. doi: 10.1007/bf01649654 [52] LI N, SHI M, GUO J Y, et al. Phys Rev Lett, 2016, 117(6): 062502. doi: 10.1103/PhysRevLett.117.062502 [53] YANG Y K, WU Y, QU Y Z, et al. Phys Lett A, 2019, 383(16): 1929. doi: 10.1016/j.physleta.2019.03.028 [54] HAGEN G, VAAGEN J S. Phys Rev C, 2006, 73(3): 034321. doi: 10.1103/PhysRevC.73.034321 [55] DELTUVA A. Few-Body Syst, 2015, 56(11-12): 897. doi: 10.1007/s00601-015-1006-8 [56] FANG Z, SHI M, GUO J Y, et al. Phys Rev C, 2017, 95(2): 024311. doi: 10.1103/PhysRevC.95.024311 [57] TIAN Y J, HENG T H, NIU Z M, et al. Chin Phys C, 2017, 41(4): 044104. doi: 10.1008/1674-1137/41/4/044104 [58] TIAN Y J, LIU Q, HENG T H, et al. Phys Rev C, 2017, 95(6): 064329. doi: 10.1103/PhysRevC.95.064329 [59] CAO X N, LIU Q, GUO J Y. J Phys G, 2018, 45(8): 085105. doi: 10.1088/1361-6471/aad0bf [60] SHI M, NIU Z M, LIANG H Z. Phys Rev C, 2018, 97(6): 064301. doi: 10.1103/PhysRevC.97.064301 [61] DING K M, SHI M, GUO J Y, et al. Phys Rev C, 2018, 98(1): 014316. doi: 10.1103/PhysRevC.98.014316 [62] CAO X N, LIU Q, GUO J Y. Phys Rev C, 2019, 99(1): 014309. doi: 10.1103/PhysRevC.99.014309 [63] CAO X N, LIU Q, NIU Z M, et al. Phys Rev C, 2019, 99(2): 024314. doi: 10.1103/PhysRevC.99.024314 [64] LUO Y X, LIU Q, GUO J Y, et al. J Phys G, 2020, 47(8): 085105. doi: 10.1088/1361-6471/ab92e2 [65] 郭建友, 刘泉, 牛中明等. 原子核物理评论, 2018, 35(4): 401. doi: 10.11804/NuclPhysRev.35.04.401 GUO J Y, LIU Q, NIU Z M, et al. Nucl Phys Rev, 2018, 35(4): 401. (in Chinese) doi: 10.11804/NuclPhysRev.35.04.401 [66] 戴华名, 曹雪能, 刘泉, 等. 原子核物理评论, 2020, 37(3): 574. doi: 10.11804/NuclPhysRev.37.2019CNPC07 DAI H M, CAO X N, LIU Q, et al. Nucl Phys Rev, 2020, 37(3): 574. (in Chinese) doi: 10.11804/NuclPhysRev.37.2019CNPC07 [67] ZHAO P W, LO Z P, YAO J M, et al. Phys Rev C, 2010, 82(5): 054319. doi: 10.1103/physrevc.82.0543119 [68] WANG Y, NIU Z M, SHI M, et al. J Phys G:Nucl Part Phys, 2019, 46: 125103. doi: 10.1088/1361-6471/ab4a9b [69] SANDULESCU N, LIOTTA R J, WYSS R. Phys Lett B, 1997, 394(1-2): 6. doi: 10.1016/S0370-2693(96)01688-7 [70] SANDULESCU N, VAN GIAI N, LIOTTA R J. Phys Rev C, 2000, 61(6): 061301(R). doi: 10.1103/physrevc.61.061301 [71] KRUPPA A T, HEENEN P H, LIOTTA R J. Phys Rev C, 2001, 63(4): 044324. doi: 10.1103/PhysRevC.63.044324 [72] CAO X N, DING K M, SHI M, et al. Phys Rev C, 2020, 102(4): 044313. doi: 10.1103/PhysRevC.102.044313 [73] ROTIVAL V, DUGUET T. Phys Rev C, 2009, 79(5): 054308. doi: 10.1103/physrevc.79.054308 [74] DUGUET T. Few-Body Syst, 2016, 57(5): 343. doi: 10.1007/s00601-016-1071-7 [75] BOHR A, MOTTELSON B R. Nuclear Structure [M]. New York: Benjamin, 1969. [76] National Nuclear Data Center[EB/OL]. [2022-04-03]. http://www.nndc.bnl.gov. [77] ANGELI I, MARINOVA K P. At. Data Nucl. Data Tables, 2013, 99(1): 69. doi: 10.1016/j.adt.2011.12.006 -








 下载:
下载:










































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号