-
横向流(tranverse flow)被用于表征重离子碰撞中核子在动量空间中各向异性的集体运动,是重离子核反应研究领域中重要的实验观测量之一[1]。横向流形成于重离子碰撞的早期,是核子-核子间强相互作用、电磁相互作用及核子-核子散射等共同作用的结果[2]。长期以来,横向流的实验研究重点关注于通过改变碰撞能量[1]、系统大小[3]、系统同位旋[4-5]及碎片质量[6]等实验条件,研究横向流随着实验条件变化的演化规律。理论研究则侧重通过调整微观输运模型的输入(包括平均场[7]、对称能[8]、核子-核子碰撞截面[9]等),研究横向流对输入参数的敏感性,并利用输运模型重现实验测量的结果,实现对平均场、对称能、核子-核子碰撞截面等横向流敏感参数的约束[1-2, 6, 10-12]。研究横向流不仅为探索重离子核反应早期的动力学机制带来机遇,也为实验上约束核物质状态方程、对称能密度依赖关系等核物理、天体物理前沿研究中涉及的关键参数提供参考。
横向流的实验测量包含碰撞实验开展、碎片探测和横向流抽取三个基本步骤。为精确测量重离子碰撞中横向流的强度,合理选择横向流的抽取方法至关重要。目前,常用的横向流抽取方法有两种:斜率法[13]和平均横动量法[14]。对于给定种类的碎片,斜率法(
$ F_{\rm slp.} $ )和平均横动量法($ F_{\rm avg.} $ )的定义式分别为$$ F_{\rm slp.} = \left. \frac{{\rm d} \langle P_{x}/A \rangle}{{\rm d}Y}\right| _{Y=0}, $$ (1) $$ F_{\rm avg.} = \frac{1}{N}\sum\limits_{i=1}^{N} S[Y(i)]\cdot\frac{P_{x}(i)}{A}, $$ (2) 式(1)中,
$ \langle P_{x}/A \rangle $ 为全体该种类的碎片在反应平面内的质心每核子横向动量在给定质心快度$ Y $ 处的平均值;式(2)中,$ P_x(i)/A $ 和$ Y(i) $ 分别为第$ i $ 个碎片在反应平面内的质心每核子横向动量和质心快度。$ S[Y(i)] $ 为第$ i $ 个碎片在质心系下的飞行取向:如碎片在质心系下向前角区飞行,$ S[Y(i)]=+1 $ ;反之,则$ S[Y(i)]=-1 $ 。由式(1)和(2)可知,在实验上利用以上两种方法抽取横向流的过程中,均需首先重建每个碰撞事件的反应平面。2016年,我们利用考虑了费米效应的反对称化量子分子动力学(AMD-FM)模型[15],研究了实验上测得的横向流碎片质量依赖关系中出现$ \alpha $ 粒子横向流异常增强[6, 16]的原因(异常的$ \alpha $ 粒子横向流见图1及其下方文字说明)。AMD-FM理论计算表明,异常$ \alpha $ 粒子横向流的产生仅与离线的反应平面重建过程相关,与碰撞动力学、激发碎片的次级衰变以及实验上近全粒子探测的限制等因素无关[16]。该结果揭示了在横向流相对碰撞能量、系统质量及系统同位旋等依赖关系的实验研究中,测量结果也可能受到“非物理因素”——反应平面重建不确定性的影响,并为进一步利用测量结果开展探究重离子核反应动力学机制、约束关键核参数等工作带来不确定性。回溯20世纪90年代,世界范围内仅少数实验室拥有4π带电粒子探测阵列(包括 MSU的Miniball/Miniwall阵列[21]、GANIL的INDRA阵列[22]等)。由于反应平面的重建需近4π空间的带电粒子探测,斜率法和平均横动量法在当时尚未被广泛应用于横向流的实验测量中。为实现中能重离子碰撞中横向流的测量,Wang等[23]提出了无需重建反应平面的双粒子方位角关联(2pAC)方法抽取横向流,即通过拟合实验上测得的2pAC函数获取重离子碰撞中横向流的强弱信息[11, 23-26]。2021年,我们在已有的2pAC方法基础上考虑了参考粒子对剩余碰撞体系的反冲效应,完成了对2pAC方法的改进和完善,具体见1.3节。利用改进的2pAC方法,研究了47 MeV/u的
$ ^{40}{\rm{Ar}} $ +$ ^{48}{\rm{Ti}} $ 碰撞中$Z = 1 \sim 4$ 碎片横向流的碎片质量依赖关系,发现了$ \alpha $ 粒子横向流异常增大的现象消失[20],且其单调的碎片质量依赖趋势与未附加额外筛选条件和处理的AMD-FM模拟结果一致。该项工作首次从实验上证明了异常的$ \alpha $ 粒子横向流与反应平面重建过程直接相关[20]。已有基于反应平面重建的横向流入射能量依赖关系的研究表明[1],中低能区的横向流强度随入射能量的增加而减弱。当入射能量增加至特定值时,平均场的吸引与核子-核子散射产生的排斥达到平衡,横向流消失,此时的入射能量称为平衡能。此后,随着入射能量的继续增加,核子-核子散射的排斥起主导作用,横向流转为正值并继续增强。平衡能的测量有助于约束核物质状态方程、对称能密度依赖关系等关键参数[1]。本文在已有横向流碎片质量依赖关系研究的基础上[20],从实验上进一步基于2pAC方法研究费米能区附近重离子碰撞中横向流随入射能量变化的依赖关系。第1节介绍实验装置及相关的离线数据分析流程,其中将详细地对2pAC横向流抽取方法及其相关的改进进行介绍。第2节给出利用2pAC方法得到的横向流的入射能量依赖关系,并讨论平衡能的测量结果。最后一节给出结论与展望。
-
本文中26, 35和47 MeV/u的
$ ^{64}{\rm{Zn}} $ 轰击$ ^{58}{\rm{Ni}} $ 靶的重离子碰撞实验于美国德州农工大学的K-500超导回旋加速器中心完成。碰撞产生的带电粒子利用Neutron Ion Multi-detector for Reaction Oriented Dynamics(NIMROD)探测,其外观见图2。NIMROD是由166个带电粒子探测单元组成的4π带电粒子探测阵列,166个单元从前角区至后角区沿束流$ z $ 轴排列成12个同轴环,整体覆盖实验室系下$ \theta_{\rm lab} $ 从$\sim 3^{\circ}$ 至$\sim 170^{\circ}$ 范围。在1号至8号环中,有两个探测单元为两块方硅和CsI(Tl)组成的“$ \varDelta E- \varDelta E-E $ ”超级望远镜系统,有三个探测单元为单块方硅和CsI(Tl)组成的“$ \varDelta E-E $ ”望远镜系统,其余探测单元均由CsI(Tl)组成。NIMROD探测单元的布局和设计见文献[27-29]。$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 碰撞产生的轻带电粒子($Z = 1 \sim 2$ )通过CsI(Tl)快慢成分法甄别,中等质量带电粒子通过“$ \varDelta E-E $ ”或“$ \varDelta E-\varDelta E $ ”法甄别。其中,超级望远镜系统的同位素分辨可至$ Z=8 $ ,望远镜系统的元素分辨可至$Z \sim 20$ 。对于仅有元素分辨的产物,$ A $ 值设为与该元素在基态丰度最大同位素相同。给定碎片的出射角度由接收该碎片探测器的几何中心和张角给出。此外,NIMROD整体被中子球[30]包裹,中子球可提供出射中子的多重性信息,本文研究未涉及使用。 -
通过初步的离线数据分析可得到碰撞事件的产物粒子表,表中记录了在每个碰撞事件中被探测粒子的
$ Z $ 、$ A $ 、出射能量和出射角度。为保证单个事件探测的完整性,首先筛选出被探测带电粒子的电荷数之和大于或等于碰撞系统电荷总数一半的事件做进一步分析。已知横向流的强弱依赖于碰撞参数的选取[4],因此需对筛选出的事件按碰撞参数进行分类。前期研究表明,在费米能区重离子碰撞中,带电粒子的多重性相比其他观测量对于碰撞参数的改变具有更强的敏感性[31]。同时,考虑到NIMROD的1号至8号环带有超级望远镜和望远镜系统,可使前角区具有较高的带电粒子探测效率,本文采用质心系下前角区的带电粒子多重性($ N_{\rm ch} $ )估算事件的碰撞参数。图3所示为归一化的
$ N_{\rm ch}/N_{\rm ch, \, Max} $ 分布图。其中,$ N_{\rm ch, \, Max}=13, 15和17 $ 分别是入射能量为26, 35和47 MeV/u的$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 碰撞在质心系下前角区测得的最大带电粒子多重性,虚线将碰撞事件从左至右分为擦边碰撞、半中心碰撞和中心碰撞三种类型。实验中,真实碰撞参数落在$ b $ 至$ b+\varDelta b $ 区间的概率正比于$ b $ ,而图中擦边碰撞事件出现的概率明显被低估,且低估的程度随入射能量的升高而增加。这主要是因为$\theta_{\rm lab} < 3.6^{\circ}$ 区域为束流管道,没有探测器覆盖。擦边碰撞以弹-靶两体作用过程为主,产生的类弹碎片质量大、出射角度较小,易沿着束流管道逃逸,且逃逸的概率会随碰撞参数的增大和入射能量的增加而增加。存在类弹碎片逃逸的擦边碰撞事件会在事件探测完整性检验的过程中被剔除。随着碰撞参数逐渐减小,碰撞从两体作用过程向更剧烈的三体过程过渡,所以对比擦边碰撞的情况,半中心碰撞和中心碰撞事件中出现逃逸类弹碎片的概率大幅降低,多数半中心碰撞和中心碰撞事件得以保留。图3中,对于半中心碰撞和中心碰撞事件,三个入射能点得到的归一化$ N_{\rm ch}/N_{\rm ch, \, Max} $ 分布图基本一致,表明在该碰撞参数范围内,26至47 MeV/u能区的$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 碰撞具有相似的反应机制,可确保利用给定的$ N_{\rm ch}/N_{\rm ch, \, Max} $ 条件在三个入射能量下筛选出相似类型的事件。为得到较强的横向流信号,本文 选择图3中两条虚线范围内的$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞事件(对应的碰撞参数范围为$ b/b_{\rm Max} $ 约$0.4 \sim 0.7$ )做后续分析,其中$ N_{\rm ch} $ 的区间选择分别为$5 \sim 9$ (26 MeV/u)、$6 \sim 10$ (35 MeV/u)和$7 \sim 12$ (47 MeV/u)。 -
2pAC方法率先由Wang等[23]提出,其独特优势在于使横向流的抽取无需预先重建每个事件的反应平面,摆脱了在反应平面重建的过程中额外引入的不确定性。目前,2pAC方法已被成功应用于几十MeV至TeV重离子碰撞的横向流研究[11, 23-26, 32]。2pAC方法基于2pAC函数建立,包括2pAC函数的重建和拟合两个步骤。根据文献[23],2pAC函数表示为
$$ C(\varDelta \phi) = \frac{N_{\rm cor}(\varDelta \phi)}{N_{\rm uncor}(\varDelta \phi)}, $$ (3) 其中:
$ N_{\rm cor}(\varDelta \phi) $ 为同一事件中任意两“关联”出射粒子的方位角夹角$ \varDelta \phi $ 分布。$ N_{\rm uncor}(\varDelta \phi) $ 为两“非关联”出射粒子的方位角夹角$ \varDelta \phi $ 分布,这里非关联粒子指分别取自任意两独立事件的两个出射粒子。$ C(\varDelta \phi) $ 可直接利用实验上测量的粒子能量和出射角度重建得到。假设每个粒子的发射相互独立,且所有出射粒子方位角$ \phi $ 的分布均服从相同分布$ F(\phi) $ ,$ C(\varDelta \phi) $ 可展开为$$C(\varDelta \phi) = \int^{2\pi}_{0} F(\phi)F(\phi+\varDelta \phi){\rm d}\phi, $$ (4) 依据文献[33],出射粒子的
$ \phi $ 分布可很好地通过二阶勒让德多项式描述:$$ \begin{array}{l} F(\varDelta \phi) = f_0\big[1+f_1\cos(\varDelta \phi)+f_2\cos(2\varDelta \phi)\big]。 \end{array} $$ (5) 其中:
$ f_0 $ 为归一化常数,由式(3)中定义可知$ C(\varDelta \phi) $ 已被归一化[23],故此处$ f_0=1 $ 。$ f_1 $ 与碰撞体系的各向异性集体运动相关,即$ f_1 $ 的绝对值越大,横向流的强度越强。$ f_2 $ 与转动集体相关。将式(5)代入式(4),可得$$ \begin{array}{l} C(\varDelta \phi) = 1+0.5f_1^2\cos(\varDelta \phi)+0.5f_2^2\cos(2\varDelta \phi)。 \end{array} $$ (6) 利用式(6)拟合实验上重建的
$ C(\varDelta \phi) $ 可得$ f_1 $ ,即得到横向流的强度。此处需强调,由式(3)~(6)推导可知,通过2pAC方法仅可获得横向流的相对强弱信息,不能获得横向流的绝对强度。然而精确测量横向流的相对强弱信息已满足本文开展横向流碰撞能量依赖关系研究的需求[20]。2000年,Prendergast等[34]发现,碰撞过程中的动量守恒会显著改变2pAC函数
$ C(\varDelta \phi) $ 的形状,而已有的2pAC方法中未考虑动量守恒效应[23],会对横向流的抽取产生潜在影响。2021年,我们通过在重建$ C(\varDelta \phi) $ 过程中修正参考粒子对剩余体系的反冲效应,考虑了动量守恒对$ C(\varDelta \phi) $ 的影响,完成了对已有2pAC方法的改进。在改进的2pAC方法中,引入反冲效应修正的基本思路如下:假设质量数为$ A_0 $ 的碰撞体系发射两个分别具有质量数$ A_1 $ 和$ A_2 $ 、质心速度$ {\boldsymbol{v_1}} $ 和$ {\boldsymbol{v_2}} $ 的关联粒子。由于2pAC方法中假设两个关联粒子的发射相互独立,关联粒子1和2可视为依次从碰撞体系出射。以粒子1作为参考粒子,当粒子1出射后,质量数为$ A_0-A_1 $ 的剩余体系将由于动量守恒获得额外的反冲速度$ \varDelta {\boldsymbol{v_r}} $ :$$ \varDelta {\boldsymbol{v_r}}= -\frac{A_1}{A_0-A_1}{\boldsymbol{v_1}}。 $$ (7) 当粒子2从剩余体系出射时,出射速度
$ {\boldsymbol{v}}_2 $ 则为碰撞动力学过程获得的本征速度$ {\boldsymbol{v_{2}}}' $ 与剩余体系的反冲速度$ \varDelta {\boldsymbol{v_r}} $ 的叠加。利用实验上测量得到的$ {\boldsymbol{v}}_2 $ 减去通过$ {\boldsymbol{v}}_1 $ 计算得到的$ \varDelta {\boldsymbol{v_r}} $ 可得$ {\boldsymbol{v_{2}}}' $ 。利用$ {\boldsymbol{v}}_1 $ 和$ {\boldsymbol{v_{2}}}' $ 即可重建出考虑了参考粒子反冲修正的2pAC函数$ C(\varDelta \phi) $ 。文献[23]指出,出射粒子生成过程中的量子统计效应和库仑相互作用也会对
$ C(\varDelta \phi) $ 的形状产生影响。为减小这两种效应的影响,在重建$ C(\varDelta \phi) $ 时选择相对动量$ \left| { \varDelta {\boldsymbol{P}}} \right|>100 $ MeV/$ c $ 的关联粒子对。此外,重建$ C(\varDelta \phi) $ 时需要考虑的另一个实验条件限制是,在质心系下同一半区(前角区或后角区)出射的关联粒子趋向于朝着同一方向飞行,两关联粒子击中同一探测器单元的概率较大。为减小此类双击事件发生的概率,进一步选取质心系下具有不同飞行取向(即$ S[Y(1)]\times S[Y(2)]=-1 $ )的关联粒子对。通过加入以上两个关联粒子的识别条件可实现对$ C(\varDelta \phi) $ 重建的进一步改进。 -
图4(a)为考虑反冲效应修正后,从26, 35和47 MeV/u的
$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞事件重建得到$ Z=1 $ 碎片的2pAC函数$ C(\varDelta \phi) $ 。由于探测器单元存在探测张角,限制了对于飞行取向不同但夹角较小的关联粒子$ \varDelta \phi $ 的测量分辨,因此如图所示在$ \varDelta \phi $ 较小的区域选择了较大的bin宽。图中,三个入射能量对应的$ C(\varDelta \phi) $ 表现出相似的单增趋势,且单增趋势随入射能量的增加逐渐变平缓。图4(b)对比给出未考虑反冲效应的$ C(\varDelta \phi) $ 结果。图中同样可观测到随$ \varDelta \phi $ 的增大表现出单调增大的趋势,以及随入射能量的增加$ C(\varDelta \phi) $ 趋于平缓的信号。
图 4 (a) 考虑反冲效应修正后,从26, 35和47 MeV/u的
$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞事件重建得到的2pAC函数$ C(\Delta \phi) $ ,(b) 同(a)未考虑反冲修正的结果(在线彩图)在图4(a)和(b)中,
$ C(\varDelta \phi) $ 的增大趋势源于碰撞过程中的横向集体运动以及任意两关联粒子具有不同飞行取向的约束[20]。由于采用了任意两关联粒子需具有不同飞行取向的约束条件,两关联粒子的方位角$ \phi $ 统计上服从对称分布$ F(\phi) $ 和$ F(\phi+180^\circ) $ ,不服从相同的分布$ F(\phi) $ 。此时,式(4)变换为$$ C(\varDelta \phi) = \int\nolimits^{2\pi}_{0} F(\phi)F(\phi+180^\circ+\varDelta \phi){\rm d}\phi , $$ (8) 推导后可得
$$ \begin{array}{l} C(\varDelta \phi) = 1-0.5f_1^2\cos(\varDelta \phi)+0.5f_2^2\cos(2\varDelta \phi) 。 \end{array} $$ (9) 利用式(9)对实验上重建的
$ C(\varDelta \phi) $ 进行拟合即可得到三个入射能量下$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 的相对横向流强弱信息,拟合结果分别见图4(a)和(b)中曲线。图5给出拟合得到的$ f_1 $ 随入射能量变化的依赖关系,$ f_1 $ 的误差为图4中拟合误差。由于拟合得到的$ f_2 $ 属小量(在$ 10^{-2} $ 量级),本文暂不对$ f_2 $ 做深入讨论,关于$ f_2 $ 的详细研究见文献[26]。已知在26~47 MeV/u能区的碰撞过程中吸引的平均场效应起主导作用,统计上会产生“负向”的横向集体运动[1],因此在拟合得到的$ f_1 $ 绝对值前添加了负号。图5中可见,$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 碰撞产生的横向流有着显著的入射能量依赖性,即横向流的强度随入射能量的增加而减弱。该横向流的强度随入射能量的增加而减弱的趋势可由吸引的平均场效应随入射能量增加而减弱解释。平均场效应的减弱使得核子-核子散射带来的排斥作用逐渐凸显出来,使得横向流强度随之减弱。图5中还可观察到,尽管横向流的强度随入射能量的增加而减弱的趋势与抽取横向流过程中是否考虑反冲修正无关,但横向流的强度却强烈依赖于反冲修正的考虑与否。由简单的两体动力学可知,在约束任意两关联粒子有不同飞行取向时,动量守恒产生的反冲效应会降低$\varDelta \phi < 90^\circ$ 的概率,提高$\varDelta \phi > 90^\circ$ 的概率。因此如图5所示,相对未考虑反冲效应的情况,考虑反冲效应后得到的横向流强度明显减弱。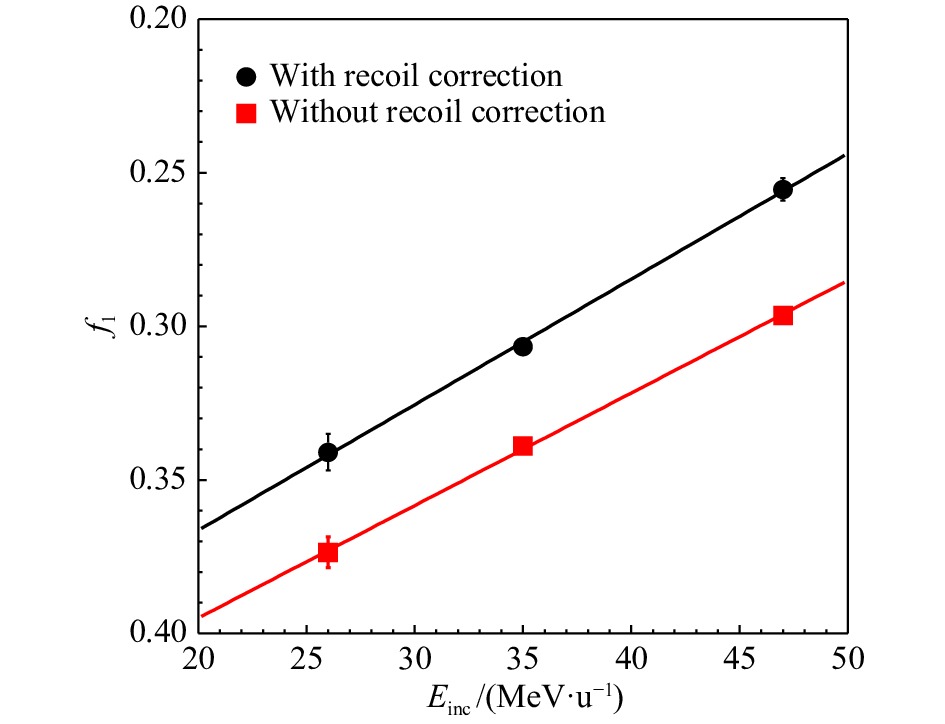
图 5 利用式(9)对实验上重建的
$ C(\Delta \phi) $ 拟合后,得到的$ f_1 $ 随入射能量变化的依赖关系(在线彩图)通过线性拟合图5结果并计算拟合直线在
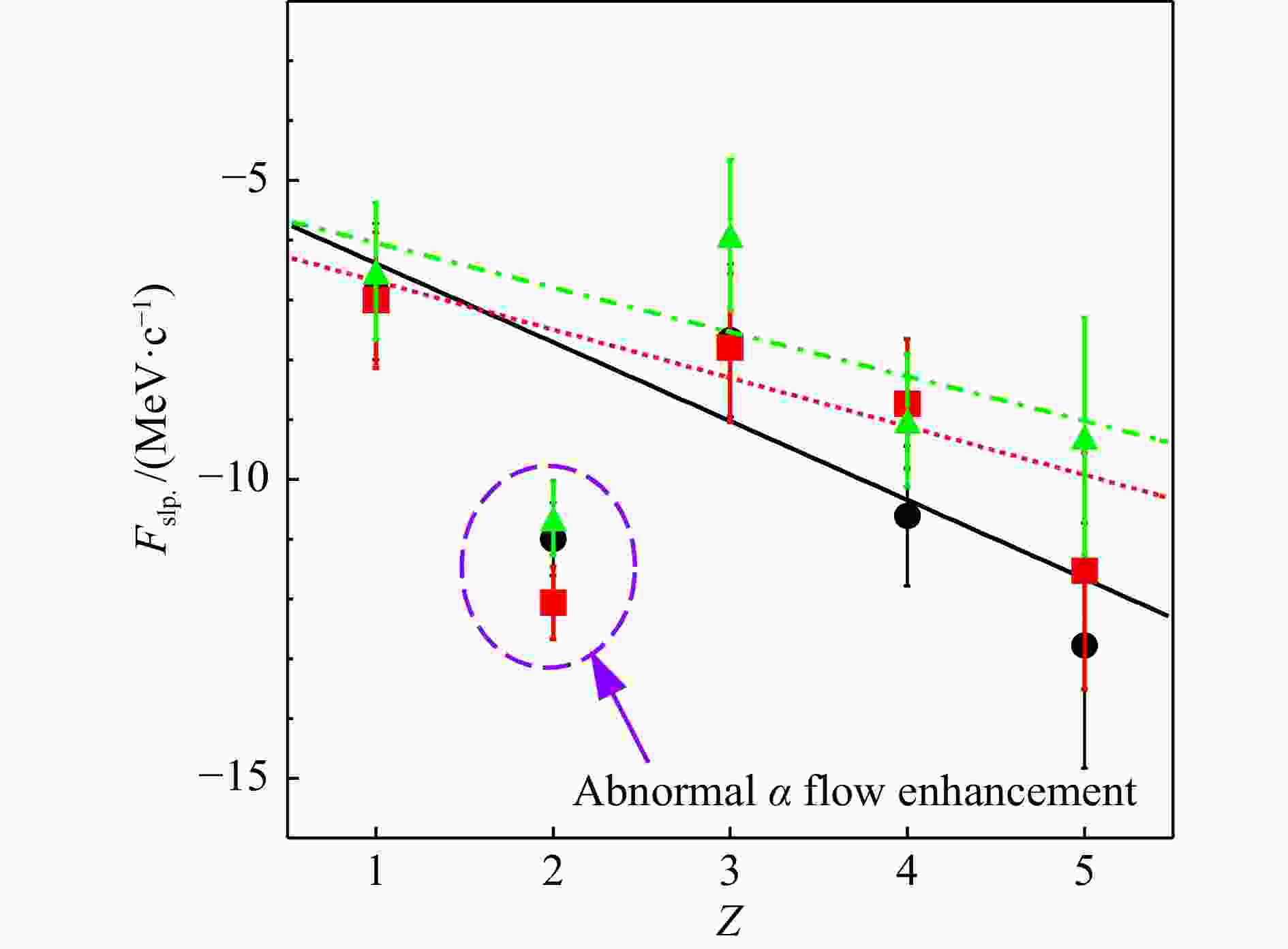
$ f_1=0 $ 处的横截距可抽取得到的$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞的平衡能。考虑和未考虑反冲修正的拟合结果如图6中红色和蓝色阴影所示。其中,阴影在$ x $ 方向展宽给出碰撞参数的不确定性,在y方向展宽为线性拟合的误差。拟合得到考虑和未考虑反冲修正的平衡能分别为$ (110.1\pm5.8) $ 和$ (128.0\pm5.6) $ MeV/u。由于平衡能具有碰撞参数依赖性[35],图6给出平衡能与碰撞参数的关系。阴影区域面积分别由线性拟合的误差和碰撞参数的区间选择决定。为做进一步比较,以往基于常规横向流抽取方法从$ ^{40}{\rm{Ar}} $ +$ ^{45}{\rm{Sc}} $ [35]、$ ^{40}{\rm{Ar}} $ +$ ^{58}{\rm{Ni}} $ [3]和$ ^{58}{\rm{Ni}} $ +$ ^{58}{\rm{Ni}} $ [3]碰撞系统测得的平衡能也绘于图6,图中直线为对已往测量结果的线性拟合。以上三个碰撞系统的大小与本文$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 碰撞系统的大小相近,可消除对比本文结果与已往实验结果时系统大小不一致带来的不确定性[36]。图中对比可见,本文基于改进的2pAC方法(考虑了反冲修正)得到的结果与以往实验测量测得的平衡能-碰撞参数关系符合得很好;相反,基于已有2pAC方法(未考虑反冲修正)得到的结果被显著高估。该结果一方面证明了在利用2pAC方法抽取横向流强度的过程中考虑反冲修正的必要性,在另一方面也证明了采用改进的2pAC方法与采用需借助反应平面重建的常规方法研究重离子碰撞的平衡能具有等价性。此外,对比常规方法,改进的2pAC方法有着明显的优势,即可以消除反应平面重建的不确定性带来的影响。因此,在未来重离子碰撞中横向流和平衡能的研究中,可优先考虑采用改进的2pAC方法。 -
本文基于双粒子方位角关联(2pAC)方法开展了26, 35和47 MeV/u的
$ ^{64}{\rm{Zn}} $ 轰击$ ^{58}{\rm{Ni}} $ 靶的重离子碰撞中横向流能量依赖关系的实验研究。通过在已有2pAC方法的基础上引入参考粒子对剩余碰撞体系的反冲效应修正并优化关联粒子的识别,改进了2pAC横向流抽取方法。利用改进的2pAC方法及已有未考虑反冲修正的2pAC方法分别抽取了三个入射能量下$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞的相对横向流强度,发现横向流的强度表现出随入射能量的增加而减弱的趋势,且该趋势与抽取横向流过程中是否考虑反冲修正无关,但考虑了反冲修正得到的横向流相对强度相比基于未考虑反冲的结果却显著减小。进一步通过线性拟合得到的相对横向流强度-入射能量关系抽取了$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞的平衡能,得到的平衡能分别为$ (110.1\pm5.8) $ MeV/u (改进的2pAC方法)和$ (128.0\pm5.6) $ MeV/u (已有的2pAC方法)。对比以往基于常规横向流抽取方法从$ ^{40}{\rm{Ar}} $ +$ ^{45}{\rm{Sc}} $ [35]、$ ^{40}{\rm{Ar}} $ +$ ^{58}{\rm{Ni}} $ [3]和$ ^{58}{\rm{Ni}} $ +$ ^{58}{\rm{Ni}} $ [3]碰撞系统测量得到的结果,发现基于改进的2pAC方法得到的结果与以往测得的平衡能-碰撞参数关系符合得很好;相反,基于已有的2pAC方法得到的结果被显著高估。该对比结果证明在利用2pAC方法抽取横向流强度的过程中考虑反冲修正的必要性,以及在平衡能研究中采用改进的2pAC方法与依赖于反应平面重建的常规方法的等价性。基于改进的2pAC方法在抽取横向流强度上具有无需重建反应平面的优势,给出在未来重离子碰撞中横向流和平衡能的研究中优先考虑采用改进的2pAC方法的建议。
Study of Transverse Flow Dependence on Incident Energy in Heavy-ion Collisions near the Fermi Energy Based on Two-particle Azimuthal Correlation Approach
-
摘要: 基于双粒子方位角关联(2pAC)方法开展了费米能区
$^{64}{\rm{Zn}} $ 轰击$^{58}{\rm{Ni}} $ 靶的重离子碰撞中横向流入射能量依赖的实验研究。利用考虑了单个事件中参考粒子对剩余体系反冲修正的改进的2pAC方法和已有的2pAC方法分别抽取了26, 35和47 MeV/u能量下$^{64}{\rm{Zn}} $ +$^{58}{\rm{Ni}} $ 半中心碰撞的相对横向流强度,发现 横向流的强度随入射能量增加而减弱的趋势与抽取横向流过程中是否考虑反冲修正无关,但考虑反冲修正时得到的横向流相对强度对比未考虑反冲修正时显著减小。通过线性拟合得到的相对横向流强度-入射能量关系,进一步获得了$^{64}{\rm{Zn}} $ +$^{58}{\rm{Ni}} $ 半中心碰撞的平衡能分别为$(110.1\pm5.8)$ MeV/u (改进的2pAC方法)和$(128.0\pm5.6)$ MeV/u (已有的2pAC方法)。对比以往基于常规反应平面重建方法抽取得到的结果发现,基于改进的2pAC方法得到的结果与以往基于常规方法测得的平衡能-碰撞参数关系符合很好;相反,基于已有2pAC方法得到的结果被显著高估。对比结果证明了在利用2pAC方法抽取横向流强度的过程中考虑反冲修正的必要性,以及在平衡能研究中采用改进的2pAC方法与依赖于反应平面重建的常规方法的等价性。-
关键词:
- 横向流的入射能量依赖 /
- 费米能区重离子碰撞 /
- 双粒子方位角关联方法 /
- 平衡能
Abstract: In this article, the incident energy dependence of transverse flow from the collisions of$^{64}{\rm{Zn}} $ +$^{58}{\rm{Ni}} $ near the Fermi energy is investigated experimentally based on a two-particle azimuthal correlation(2pAC) approach. The transverse flow values from the mid-peripheral collisions at the incident energies of 26, 35 and 47 MeV/u are extracted using the 2pAC approaches with and without the specific consideration of the recoil effect from the emitted particle of interest to the residue in an event-by-event basis, respectively. The flow values extracted from both approaches show consistently increasing trend as a function of incident energy. In contrast, the flow values for the three energies show different in magnitude, that those from the improved 2pAC approach with the consideration of the recoil effect are significantly reduced. The balance energy of the mid-peripheral$^{64}{\rm{Zn}} $ +$^{58}{\rm{Ni}} $ collisions is further investigated using linear fit for the obtained transverse flow versus incident energy, and two balance energy values are obtained to be$(110.1\pm5.8)$ MeV/u for the improved 2pAC approach and$(128.0\pm5.6)$ MeV/u for the original 2pAC approach, respectively. These two values are compared with those previously measured based on the conventional flow extraction approach involving the reaction plane reconstruction process. It is found that the balance energy from the improved 2pAC approach, rather than that from the original 2pAC approach, follows well the relation of balance energy versus impact parameter from the conventional approach. This comparison suggests the necessity for considering the recoil effect correction in the flow extraction using the 2pAC approach, and the equivalence between the improved 2pAC approach and the conventional flow extraction approach involving the reaction plane reconstruction process in the investigation on the balance energy. -
图 4 (a) 考虑反冲效应修正后,从26, 35和47 MeV/u的
$ ^{64}{\rm{Zn}} $ +$ ^{58}{\rm{Ni}} $ 半中心碰撞事件重建得到的2pAC函数$ C(\Delta \phi) $ ,(b) 同(a)未考虑反冲修正的结果(在线彩图)(a)和(b)中数据点$ y $方向的误差为统计误差,曲线为利用式(9)对实验上重建结果的拟合。
图 5 利用式(9)对实验上重建的
$ C(\Delta \phi) $ 拟合后,得到的$ f_1 $ 随入射能量变化的依赖关系(在线彩图)其中,实心圆和实心正方形分别为考虑了反冲修正和未考虑了反冲修正的结果,直线分别为对结果的线性拟合。
-
[1] DANIELEWICZ P, LACEY R, LYNCH W G. Sci, 2002, 298: 1592. doi: 10.1126/science.1078070 [2] LI B A, CHEN L W, KO C M. Phys Rep, 2008, 464: 113. doi: 10.1016/j.physrep.2008.04.005 [3] CUSSOL D, LEFORT T, PETER J, et al. Phys Rev C, 2002, 65: 044604. doi: 10.1103/PhysRevC.65.044604 [4] PAK R, BENENSON W, BJARKI O, et al. Phys Rev Lett, 1997, 78: 1022. doi: 10.1103/PhysRevLett.78.1022 [5] PAK R, LI B A, BENENSON W, et al. Phys Rev Lett, 1997, 78: 1026. doi: 10.1103/PhysRevLett.78.1026 [6] LIU X, LIN W, WADA R, et al. Phys Rev C, 2014, 90: 014604. doi: 10.1103/PhysRevC.90.014604 [7] CHUGH R, PURI R K. Phys Rev C, 2010, 82: 014603. doi: 10.1103/PhysRevC.82.014603 [8] GAUTAM S, SOOD A D, PURI R K, et al. Phys Rev C, 2011, 83: 034606. doi: 10.1103/PhysRevC.83.034606 [9] SOOD A D, PURI R K. Phys Rev C, 2006, 73: 067602. doi: 10.1103/PhysRevC.73.067602 [10] ONO A, HORIUCHI H. Phys Rev C, 1995, 51: 299. doi: 10.1103/PhysRevC.51.299 [11] CHEN L W, ZHANG F S, ZHU Z Y. Phys Rev C, 2000, 61: 067601. doi: 10.1103/PhysRevC.61.067601 [12] KOHLEY Z, COLONNA M, BONASERA A, et al. Phys Rev C, 2012, 85: 064605. doi: 10.1103/PhysRevC.85.064605 [13] WESTFALL G D. Nucl Phys A, 1998, 630: 27. doi: 10.1016/S0375-9474(97)00741-0 [14] BONASERA A, GULMINELLI F, MOLITORIS J. Phys Rep, 1994, 243: 1. doi: 10.1016/0370-1573(94)90108-2 [15] LIN W, LIU X, WADA R, et al. Phys Rev C, 2016, 94: 064609. doi: 10.1103/PhysRevC.94.064609 [16] QU G, HUANG Y, PENG D, et al. Phys Rev C, 2021, 103: 044607. doi: 10.1103/PhysRevC.103.044607 [17] CUGNON J, L’HOTE D. Nucl Phys A, 1983, 397: 519. doi: 10.1016/0375-9474(83)90614-0 [18] DANIELEWICZ P, ODYNIEC G. Phys Lett B, 1985, 157: 146. doi: 10.1016/0370-2693(85)91535-7 [19] WILSON W K, LACEY R, OGILVIE C A, et al. Phys Rev C, 1992, 45: 738. doi: 10.1103/PhysRevC.45.738 [20] HUANG Y, LIN W, ZHENG H, et al. Phys Rev C, 2021, 104: 044611. doi: 10.1103/PhysRevC.104.044611 [21] DE SOUZA R T, CARLIN N, KIM Y D, et al. Nucl Instr and Meth A, 1990, 295: 109. doi: 10.1016/0168-9002(90)90429-A [22] POUTHAS J, BORDERIE B, DAYRAS R, et al. Nucl Instrum Methods Phys Res Sect A, 1995, 357: 418. doi: 10.1016/0168-9002(94)01543-0 [23] WANG S, JIANG Y Z, LIU Y M, et al. Phys Rev C, 1991, 44: 1091. doi: 10.1103/PhysRevC.44.1091 [24] LACEY R A, ELMAANI A, LAURET J, et al. Phys Rev Lett, 1993, 70: 1224. doi: 10.1103/PhysRevLett.70.1224 [25] SINGH G, JAIN P L. Phys Rev C, 1994, 49: 3320. doi: 10.1103/PhysRevC.49.3320 [26] MA Y G, SHEN W Q. Phys Rev C, 1995, 51: 3256. doi: 10.1103/PhysRevC.51.3256 [27] WADA R, KEUTGEN T, HAGEL K, et al. Phys Rev C, 2004, 69: 044610. doi: 10.1103/PhysRevC.69.044610 [28] MA Y G, NATOWITZ J B, WADA R, et al. Phys Rev C, 2005, 71: 054606. doi: 10.1103/PhysRevC.71.054606 [29] WANG J S, WADA R, KEUTGEN T, et al. Phys Rev C, 2005, 72: 024603. doi: 10.1103/PhysRevC.72.024603 [30] SCHMITT R P, COOKE L, DERRIG G, et al. Nucl Instr and Meth A, 1995, 354: 487. doi: 10.1016/0168-9002(94)01029-3 [31] ZHANG X, LIU X, HUANG Y, et al. Phys Rev C, 2022, 105: 034611. doi: 10.1103/PhysRevC.105.034611 [32] DORDEVIC M, MILOSEVIC J, NADDERD L, et al. Phys Rev C, 2020, 101: 014908. doi: 10.1103/PhysRevC.101.014908 [33] TSANG M B, DANIELEWICZ P, BOWMAN D R, et al. Phys Lett B, 1992, 297: 243. doi: 10.1016/0370-2693(92)91256-9 [34] PRENDERGAST E P, VAN DEN BRINK A, DE HAAS A P, et al. Phys Rev C, 2000, 61: 024611. doi: 10.1103/PhysRevC.61.024611 [35] WESTFALL G D. Nucl Phys A, 2001, 681: 343c. doi: 10.1016/S0375-9474(00)00538-8 [36] SOOD A D, PURI R K. Phys Rev C, 2004, 69: 054612. doi: 10.1103/PhysRevC.69.054612 -
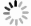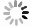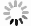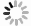














 下载:
下载:



















































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号