-
原子核质量在原子核结构、核天体物理及基本相互作用和对称性检验等研究领域有重要应用,因此原子核质量测量一直是核物理研究的前沿课题之一[1-2]。当前质量未知或质量测量误差较大的原子核大都是远离
$ \beta $ 稳定线的奇特核,它们的寿命极短、产额极低,测量这些原子核的质量需要发展快速高效的实验方法。基于储存环的等时性质谱术(Isochronous Mass Spectrometry, IMS)具有毫秒以内的短测量时间,是高精度测量极短寿命原子核质量的理想工具。目前能够开展等时性质量测量的储存环有德国亥姆霍兹重离子加速器研究中心(GSI)的实验储存环(ESR)[3-4],中国科学院近代物理研究所的实验冷却储存环(CSRe)[5-7],日本理化学研究所(RIKEN)的稀有放射性同位素环(R3)[8-9]。飞行在储存环中的离子,其质荷比
$ m/q $ ,循环周期$ T $ 以及磁刚度$ B\rho $ 有如下关系:$$ \frac{m}{q} = B\rho\sqrt{ \left(\frac{T}{C} \right)^2-\frac{1}{c^2}}, $$ (1) 其中:
$ C $ 是离子在环中循环一周的轨道长度;$ c $ 是真空中的光速。$ C $ 与$ B\rho $ 相互关联,当$ B\rho $ 为确定值时,相应的$ C $ 也就固定了。假定所有存储的离子具有相同的$ B\rho $ ,离子的质荷比$ m/q $ 与循环周期$ T $ 存在一一对应关系。在实际测量中,通常利用已知质量的核素建立起$ m/q\sim T $ 关系的质量刻度方程,并将实验测得的目标核的$ T $ 代入刻度方程得到其质量。由于储存环具有一定的磁刚度接收度$ \varDelta B\rho/B\rho $ ,对于某一种原子核,其磁刚度的变化会引起循环周期的变化,在一阶近似下,循环周期的相对变化表示为[4]$$ \frac{\varDelta T}{T} = - \left(\frac{1}{\gamma^2}-\frac{1}{\gamma_{\rm{t}}^2} \right)\frac{\varDelta B\rho}{B\rho} = -\eta\frac{\varDelta B\rho}{B\rho}, $$ (2) 其中:
$ \eta $ 称为滑相因子;$ \gamma $ 是离子的相对论洛伦兹因子;$ \gamma_{\rm{t}}^{} $ 是储存环转变能参数(transition energy)。在等时性质量测量实验中,要求注入储存环的目标离子满足$ \gamma = \gamma_{\rm{t}}^{} $ ,此时,目标原子核的循环周期与其磁刚度分散无关。但是当某种原子核$ \gamma\neq \gamma_{\rm{t}}^{} $ 时,其循环周期受到磁刚度分散的影响[10]。我们将仅测量离子的循环周期,并通过$ \gamma = \gamma_{\rm{t}}^{} $ 设置进行的质量测量称之为常规IMS。在过去的十多年中,我们在缺中子核区进行了多次质量测量实验,发现常规IMS存在一些问题。其一,随着离子
$ \gamma $ 远离$ \gamma_{\rm{t}}^{} $ ,动量分散对循环周期的影响迅速增大,相应地,质量分辨能力迅速降低[10-11]。其二,更为严重的问题是,在较宽的时域,质量测量结果存在系统性偏差。系统性偏差的存在迫使我们只能使用等时性窗口内的实验数据。当循环周期远离等时性窗口时,质量测量结果的可靠性会大大降低[12-14]。系统性偏差不同于系统误差,不能简单地通过给质量测量结果引入系统误差来解决。在CSRe上开展的等时性质量测量实验中,为了避免系统性偏差对质量测量结果的影响,通常只使用同一同位旋$ T_z^{} $ 系列的原子核来确定质量[7],即:利用同一$ T_z^{} $ 系列的原子核做质量刻度,以此刻度公式确定同一$ T_z^{} $ 系列未知质量的核素质量。或者只确定等时性窗口[15]内很窄的循环周期范围的原子核质量[16-17]。利用这些方法,在之前的CSRe质量测量结果中,没有发现明显的系统性偏差。ESR报导的等时性质量测量结果中,普遍存在百keV量级的系统误差[18-19],这可能也来源于质量测量的系统性偏差,由于注入储存环的丰中子弹核碎片中,同一$ T_z^{} $ 系列原子核种类都较少,所以系统性偏差的同位旋依赖性没有体现出来。基于我们多年数据分析经验和模拟研究[12-14],质量测量结果的系统性偏差主要来源于注入储存环的不同种类原子核具有不同形状的动量分布(或磁刚度分布),使得不同原子核的平均循环周期对应于不同的平均磁刚度;另外,滑相因子
$ \eta $ ,不同$ T_z^{} $ 的离子穿过碳膜时具有不同的能损,以及储存环$\gamma_{\rm{t}}^{}$ 随磁刚度变化等因素也会引起质量测量结果的系统性偏差。迄今为止,还没有基于实验测量数据,研究离子的磁刚度分布对质量测量系统性偏差影响的工作。最近,我们在CSRe的一个直线段上安装了两个相距约18 m的飞行时间(TOF)探测器[20],实现了环内离子循环周期和速度的同时测量[21],从而得到了离子的磁刚度。
本工作将利用双TOF探测器测量的58Ni碎片的周期和速度,给出已知质量核素的磁刚度分布。通过实验数据选择来限制离子的磁刚度,重新构建不同磁刚度区间的循环周期谱,再按照常规IMS的数据分析方法确定核素质量,研究系统性偏差的变化,旨在从实验上证实常规IMS质量测量系统性偏差的来源。
-
实验是在兰州重离子加速器冷却储存环装置上开展的,能量为428 MeV/u的主束58Ni19+在放射性束流线RIBLL2的入口处轰击15 mm厚的9Be靶,弹核碎裂产物经RIBLL2分离、筛选后注入并储存在CSRe中。CSRe设置在等时性光学模式下
$ \gamma_{\rm{t}}^{} = 1.36 $ ,磁刚度接收度为$\pm0.2{\text{%}}$ 。RIBLL2-CSRe中心磁刚度设置为5.471 Tm。飞行在环内的离子经过TOF探测器[22]时,会在碳膜上激发出二次电子,二次电子被匀强电磁场加速偏转到微通道板(MCP)上,倍增放大后的信号由高频同轴电缆传输到示波器以50 GHz的采样率记录下来。一个离子在两个TOF探测器上分别产生一个时间(
$ t $ )-圈数($ N $ )序列$ t_{\rm{TOF1}}^{}(N) $ 和$ t_{\rm{TOF2}}^{}(N) $ ,从这两个$ t $ -$ N $ 序列可以提取速度$ v $ ,由以下公式求出:$$ v = \frac{L}{t_{\rm{TOF2}}^{}-t_{\rm{TOF1}}^{}+\varDelta t_{\rm{d}}^{}}, $$ (3) 其中:
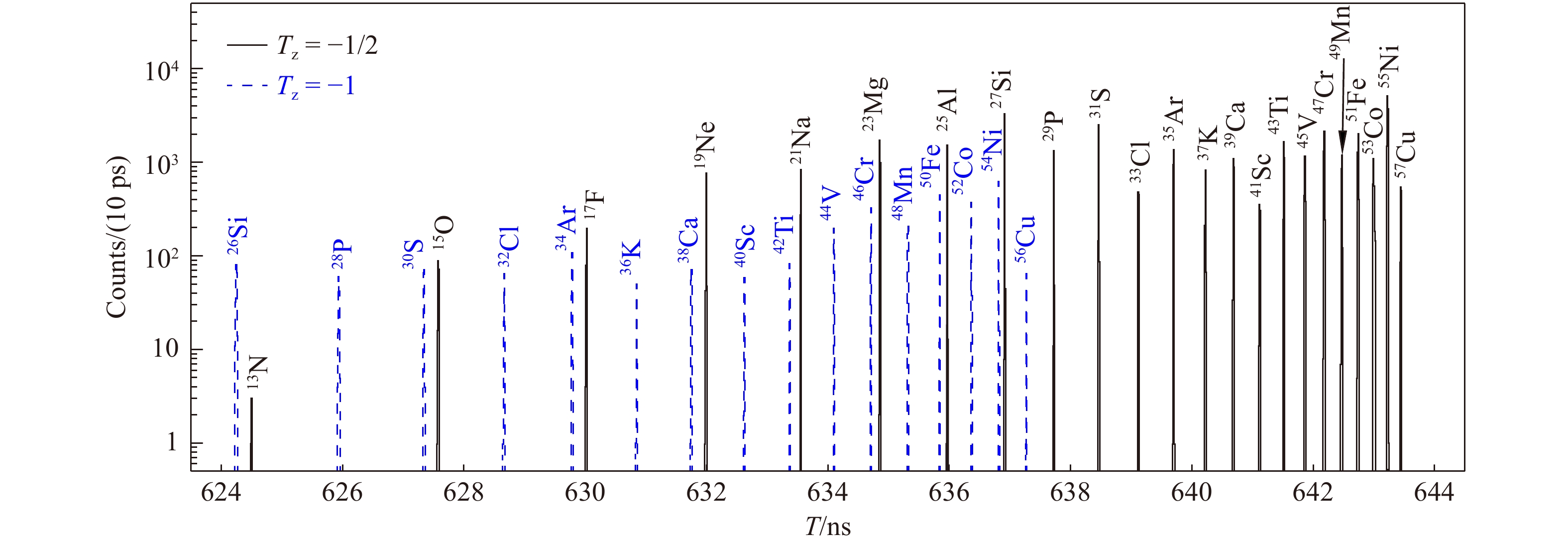
$ L $ 是两个TOF探测器之间的距离;$ \varDelta t_{\rm{d}}^{} $ 是两路信号从探测器到示波器的传输时间差,详见参考文献[21, 23]。离子的循环周期$ T $ 则由$ t $ -$ N $ 序列的斜率给出[24],图1是本次实验得到的循环周期谱,粒子鉴别参考文献[24]的方法,实验主要产生了$ T_z^{} = -1/2 $ 和$ -1 $ 两个不同系列的原子核。后续分析中,每一种原子核的循环周期由相应循环周期峰的算术平均值给出。 -
我们用LISE++程序[25],模拟了在本次实验条件下,注入到CSRe中的离子的磁刚度分布,如图2所示。
$ T_z^{} = -1/2 $ 的原子核在环内的磁刚度分布是不对称的,而$ T_z^{} = -1 $ 系列原子核则更接近于对称分布,即不同$ T_z^{} $ 系列的原子核磁刚度分布具有不同程度的不对称性。
图 2 LISE++程序[25]模拟得到的注入CSRe的部分原子核磁刚度分布(在线彩图)
对于一个质荷比为
$ m/q $ ,速度为$ v $ 的离子,其磁刚度为$$ B\rho = \frac{m}{q}\gamma v \text{。} $$ (4) 利用实验测量的离子速度,根据式(4)计算得到所有质量已知[26]且质量误差小于12 keV核素的磁刚度。图3展示的是55Ni(
$ T_z^{} = -1/2 $ )和54Ni($ T_z^{} = -1 $ )的磁刚度分布,分布底宽符合$\pm0.2 \text{%}$ 的磁刚度接收度,且与LISE++[25]模拟结果(图2)的不对称性一致。从图2和图3中可以看到,
$ T_z^{} = -1/2 $ 系列原子核的平均磁刚度要大于$ T_z^{} = -1 $ 系列原子核。我们从实验数据中提取了不同原子核平均循环周期$ T $ 与平均磁刚度$ \overline{B\rho} $ 的关系,结果展示在图4(a)中。从图中可以看到,相近的平均循环周期下,$ T_z^{} = -1/2 $ 系列原子核的平均磁刚度要大于$ T_z^{} = -1 $ 系列原子核。因此利用同一个质量刻度公式定出的质量结果显而易见就会出现系统性偏差。 -
通过对实验测量的周期谱进行分析,可以得到目标核的质量(或
$ m/q $ 值)。原则上讲,对于如图1所示的周期谱,可以用任何已知质量的核素对周期谱进行刻度。为了凸显常规IMS的系统性偏差,我们用$ T_z^{} = -1/2 $ 的原子核作为参考离子刻度周期谱,即确定质荷比$ m/q $ 与循环周期$ T $ 的关系:$$ m/q(T) = a_0^{}+a_1^{}T+a_2^{}T^2+a_3^{}T^3, $$ (5) 其中
$ a_i\; (i = 0,\,1,\,2,\,3) $ 是拟合参数。详细刻度过程参考文献[27-28]。为了检验质量刻度的可靠性,所有
$ N_{\rm{c}}^{} $ 个参考核都分别被当作质量未知核,使用其他$ N_{\rm{c}}^{}-1 $ 个刻度核根据以上步骤重新确定了质量,将重新确定的质量与文献值进行比较,定义归一化卡方$$ {\chi ^{}_{\rm{n}}} = \sqrt {\frac{1}{{N_{\rm{c}}}}\sum\limits_{i = 1}^{N_{\rm{c}}} {\frac{{{{({\rm{ME}}{{\rm{}}_{{\rm{exp}},{\kern 1pt} i}}{\rm{ - ME}}{{\rm{}}_{{\rm{AME}},{\kern 1pt} i}})}^{\rm{2}}}}}{{\sigma _{{\rm{exp}},{\kern 1pt} i}^2 + \sigma _{{\rm{AME}},{\kern 1pt} i}^2}}} } , $$ (6) 其中
$ {\rm{ME}} = M-Au $ 是原子质量过剩。当$ \chi_{\rm{n}}^{} = 1\pm1/\sqrt{2N_{\rm{c}}^{}} $ 时,表示不需要考虑额外的系统误差。否则需要引入系统误差,即在式(6)的分母加上$ \sigma_{\rm{sys}}^2 $ 使$ \chi_{\rm{n}}^{} = 1 $ 。本文利用
$ T_z^{} = -1/2 $ 从15O到49Mn的$ N_{\rm{c}}^{} = 16 $ 种1 原子核作为参考核来刻度质荷比与循环周期的关系式(5),重新确定出$ T_z^{} = -1 $ 原子核的质量,并与文献值[26]进行比较。图5(a)是本次实验全接收度内的数据得到的质量过剩值$ {\rm{M}}{{\rm{E}}_{{\rm{exp}}}^{}} $ 与AME2020[26]质量过剩值${\rm{M}}{{\rm{E}}_{{\rm{AME2020}}}^{}} $ 的比较。从图5(a)可以看到,重新确定的$ T_z^{} = -1 $ 原子核的质量与文献值相比存在明显的系统性偏差。这个系统性偏差主要来源于动量分布(或磁刚度分布)的不对称性2 ,这导致不同原子核具有不同的平均磁刚度[见图4(a)]。系统性偏差在以往的实验中也看到过[12-14],因此在以往实验中只考虑等时性中心很小的循环周期范围内的原子核进行质量刻度,或者通过机械狭缝限制储存环动量接收度[28, 31-33]来部分消除这种系统性偏差。本次实验中,我们可以直接得到每个质量已知离子的磁刚度,从而可以利用选择磁刚度区间(或轨道长度区间)来限制磁刚度接收度,使得宽质荷比范围内的原子核具有相同的平均磁刚度,从而验证在常规IMS质量测量实验中,限制动量接收度以消除系统性偏差这种方法的有效性。 -
飞行在储存环中的任意离子,其磁刚度
$ B\rho $ 和轨道长度$ C = Tv $ 都在同一个$ B\rho\sim C $ 曲线上,且与离子种类无关。图6是所有质量已知离子的$ B\rho $ 与$ C $ 的变化关系,可以看到不同种类离子的$ B\rho $ 与$ C $ 在同一个$ B\rho\sim C $ 曲线附近。实验中,满足储存环磁刚度接收度的离子都会被注入CSRe中,所有种类的原子核磁刚度$ B\rho $ 都分布在(5.465, 5.488) Tm的区间内,磁刚度接收度为$\pm0.2\text{%}$ ,对应的轨道长度$ C $ 区间为(128.73, 129.04) m。为了研究不同磁刚度下质量测量结果的系统性偏差,我们对离子的轨道长度加以限制,即选取轨道长度在(128.8, 128.95) m和(128.848, 128.914) m区间的离子,重新构建周期谱,得到不同磁刚度区间(5.471 5, 5.482 5)Tm和(5.474 8, 5.480 2) Tm下的周期谱,对应的磁刚度接收度为
$\pm0.1\text{%}$ 和$\pm0.04\text{%}$ ,如图6中灰色和绿色区域。限制磁刚度接收度后55Ni($T_z^{} = -1/2$ )和54Ni$( T_z^{} = -1)$ 的磁刚度分布如图3中灰色阴影($\varDelta B\rho/B\rho = \pm0.1\text{%}$ )和绿色阴影($\varDelta B\rho/B\rho = \pm0.04\text{%}$ )覆盖区域所示,随着磁刚度接收度的减小,两种原子核的平均磁刚度逐渐接近。从限制磁刚度接收度为
$ \pm0.1\% $ 和$\pm0.04\text{%}$ 的周期谱上,提取出不同种类原子核的平均循环周期以及相应的平均磁刚度,结果展示在图4(b)和(c)中。从图4(c)可以看到,所有原子核的平均磁刚度几乎都相同,即可以认为此区间内的原子核具有相同的平均磁刚度。针对重新构建的周期谱,按照上述方法,用16个$ T_z^{} = -1/2 $ 核素进行刻度,重新得到$ T_z^{} = -1 $ 核素的质量,结果展示在图5(b)和(c)。相比于图5(a),图5(b)中质量测量结果的系统性偏差大大减小。图5(c)中系统性偏差被完全消除,$ \chi_{\rm n}^{} $ 由1.31降为1.00,表明不再需要考虑额外的系统误差,质量测量结果可靠。限制磁刚度接收度后,等时性中心外的原子核的质量分辨能力也得到了提高,图7是限制磁刚度接收度前后循环周期标准偏差
$ \sigma_T^{} $ 与循环周期的变化关系。从图中可以看出,对于等时性中心的原子核,限制磁刚度接收度对于循环周期标准偏差影响不大。对于远离等时性中心的核素,限制磁刚度接收度后$ \sigma_T^{} $ 逐渐减小,分辨能力提高,在距离等时性中心约10 ns处,$\varDelta B\rho/B\rho = \pm0.04\text{%}$ 时的$ \sigma_T^{} $ 是全接收度时的$ 1/3.5 $ ,即限制磁刚度接收度为$\varDelta B\rho/B\rho = \pm0.04\text{%}$ 时,距离等时性中心约10 ns处的质量分辨能力是原来的3.5倍。从以上研究可以看出,限制磁刚度接收度后,质量测量结果的系统性偏差得到了消除,提高了质量测量结果的可靠性;减小了循环周期峰的标准偏差,提高了宽循环周期范围内的质量分辨能力。但是质量分辨能力和质量测量结果可靠性的提高都是以损失大量离子统计为代价的,图8展示了每种原子核在限制磁刚度接收度为
$\varDelta B\rho/B\rho = \pm0.04\text{%}$ 后的计数$ N $ 与原有计数$ N_0^{} $ 的比值$ N/N_0^{} $ ,在限制磁刚度接收度后,大部分原子核统计都只有原来的20%~30%,这非常不利于低产额原子核的质量测量。 -
为了从实验上研究常规IMS质量测量的系统性偏差,我们利用安装在CSRe直线段的双TOF探测器,测量了环内离子速度和循环周期。利用离子速度和质量从实验上得到离子磁刚度(或动量)分布。发现原子核磁刚度分布呈不同程度的非对称性,即:不同原子核具有不同的平均磁刚度,这造成了质量测量的系统性偏差。本次实验中,
$ T_z^{} = -1/2 $ 系列原子核的平均磁刚度大于相近循环周期的$ T_z^{} = -1 $ 系列原子核的平均磁刚度,从而使用$ T_z^{} = -1/2 $ 系列原子核刻度周期谱,重新确定的$ T_z^{} = -1 $ 系列原子核质量存在系统性的偏差。利用测量的磁刚度信息限制磁刚度接收度,磁刚度接收度越小,质量测量结果的系统性偏差就越小。当接收度为
$\varDelta B\rho/B\rho = \pm0.04\text{%}$ 时,不同原子核的平均循环周期都对应近似同一个平均磁刚度,从而消除了质量测量结果的系统性偏差。最终,同时提高了$ \varDelta T\approx20 $ ns的宽循环周期范围内的质量分辨能力和质量测量结果可靠性。限制磁刚度接收度消除动量分散对质量测量影响的方法不可避免地会损失大量离子统计,不利于远离
$ \beta $ 稳定线的极低产额原子核的质量测量。我们新建立了基于双TOF探测器开发的新型等时性质谱术—磁刚度识别IMS($ B\rho $ -IMS),其数据处理方法和结果将另文做详细介绍。$ B\rho $ -IMS将充分利用离子的循环周期和速度信息,在不损失离子统计的情况下提高宽循环周期范围内的质量分辨能力及质量测量结果的可靠性,是高精度测量短寿命、低产额原子核质量的理想工具,将会是未来储存环质谱术的发展方向。
Experimental Study on the Systematic Deviation in the Conventional Isochronous Mass Spectrometry
-
摘要: 基于重离子储存环建立的等时性质谱术(IMS)是测量远离稳定线核素质量的有效工具。但是,采用常规IMS测量缺中子一侧的核素质量时,发现
$T_z^{}=-1/2$ 和$T_z^{}=-1$ 核素的质量测量结果在宽时域范围内存在系统性偏差。本工作利用CSRe直线段上的双飞行时间(TOF)探测器,同时测量了循环离子的周期和速度。利用这些实验信息,对常规IMS质量测量中出现的系统性偏差进行了研究。发现系统偏差是由于储存的离子动量分布不对称以及储存环能量转变参数$\gamma_{\rm t}^{}$ 非恒定造成的。在离线数据处理时,发现通过限制动量接收度的大小,可以消除常规IMS质量测量中的系统偏差。这一结果对采用常规IMS进行质量测量具有重要参考价值和指导意义。Abstract: Storage-ring-based isochronous mass spectrometry(IMS) is an effective tool for mass measurements of nuclei far from stability line. However, in the mass measurements of neutron-deficient nuclei with conventional IMS, systematic deviation of mass determination was observed when nuclei with$T_z^{}=-1/2$ and$T_z^{}=-1$ in a wide revolution time range were measured. In this work, the revolution time and velocity of stored ions were measured simultaneously by using two time-of-flight(TOF) detectors installed in a straight section of CSRe. Using these experimental information, systematic deviation in conventional IMS was investigated experimentally. The systematic deviation is found to be caused by the different asymmetric distributions of momentum of the stored ions and the non-constant storage ring energy transition parameter$\gamma_{\rm t}^{}$ , and it can be eliminated by limiting the momentum acceptance during offline data processing. This study provides valuable reference and significant guidance for mass measurements using conventional IMS. -
图 2 LISE++程序[25]模拟得到的注入CSRe的部分原子核磁刚度分布(在线彩图)
绿色虚线表示$\pm0.2\text{%}$的磁刚度接收度。
-
[1] BLAUM K. Physics Reports, 2006, 425(1): 1. doi: 10.1016/j.physrep.2005.10.011 [2] YAMAGUCHI T, KOURA H, LITVINOV Y, et al. Progress in Particle and Nuclear Physics, 2021, 120: 103882. doi: 10.1016/j.ppnp.2021.103882 [3] FRANZKE B. Nucl Instr and Meth B, 1987, 24-25: 18. doi: 10.1016/0168-583X(87)90583-0 [4] HAUSMANN M, ATTALLAH F, BECKERT K, et al. Nucl Instr and Meth A, 2000, 446(3): 569. doi: 10.1016/S0168-9002(99)01192-4 [5] XIA J W, ZHAN W L, WEI B W, et al. Nucl Instr and Meth A, 2002, 488(1): 11. doi: 10.1016/S0168-9002(02)00475-8 [6] YUAN Y J, YANG J C, XIA J W, et al. Nucl Instr and Meth B, 2013, 317: 214. doi: 10.1016/j.nimb.2013.07.040 [7] TU X L, XU H S, WANG M, et al. Phys Rev Lett, 2011, 106: 112501. doi: 10.1103/PhysRevLett.106.112501 [8] YAMAGUCHI Y, WAKASUGI M, UESAKA T, et al. Nucl Instr and Meth B, 2013, 317: 629. doi: 10.1016/j.nimb.2013.06.004 [9] LI H F, NAIMI S, SPROUSE T M, et al. Phys Rev Lett, 2022, 128: 152701. doi: 10.1103/PhysRevLett.128.152701 [10] ZHANG Y H, LITVINOV Y A, UESAKA T, et al. Physica Scripta, 2016, 91(7): 073002. doi: 10.1088/0031-8949/91/7/073002 [11] XU H S, ZHANG Y H, LITVINOV Y A. International Journal of Mass Spectrometry, 2013, 349-350: 162. doi: 10.1016/j.ijms.2013.04.029 [12] 臧永东. 58Ni 碎片质量测量数据处理方法[D]. 北京: 中国科学院研究生院, 2011. ZANG Yongdong. Data Analysis of Isochronous Mass Measurement via 58Ni Fragmentation[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2011. (in Chinese) [13] 徐星. HIRFL-CSR 上短寿命丰中子核素的精确质量测量[D]. 北京: 中国科学院大学, 2015. XU Xing. Precise Mass Measurement of Short-lived Neutron-rich Nuclei at HIRFL-CSR[D]. Beijing: University of Chinese Academy of Sciences, 2015. (in Chinese) [14] 帅鹏. HIRFL-CSR 上短寿命核素质量的精确测量[D]. 北京: 中国科学院大学, 2014. SHUAI Peng. Accurate Mass Measurements of Short-lived Nuclides at the HIRFL-CSR Facility[D]. Beijing: University of Science and Technology of China, 2014. (in Chinese) [15] XU X, WANG M, ZHANG Y H, et al. Chin Phys C, 2015, 39(10): 104001. doi: 10.1088/1674-1137/39/10/104001 [16] ZHANG Y H, XU H S, LITVINOV Y A, et al. Phys Rev Lett, 2012, 109: 102501. doi: 10.1103/PhysRevLett.109.102501 [17] YAN X L, XU H S, LITVINOV Y A, et al. The Astrophysical Journal Letters, 2013, 766(1): L8. doi: 10.1088/2041-8205/766/1/l8 [18] SUN B, KNÖBEL R, LITVINOV Y, et al. Nuclear Physics A, 2008, 812(1): 1. doi: 10.1016/j.nuclphysa.2008.08.013 [19] KNÖBEL R, DIWISCH M, BOSCH F, et al. Phys Lett B, 2016, 754: 288. doi: 10.1016/j.physletb.2016.01.039 [20] XING Y M, WANG M, ZHANG Y H, et al. Physica Scripta, 2015, T166: 014010. doi: 10.1088/0031-8949/2015/t166/014010 [21] ZHOU X, ZHANG M, WANG M, et al. Phys Rev Accel Beams, 2021, 24: 042802. doi: 10.1103/PhysRevAccelBeams.24.042802 [22] ZHANG W, TU X, WANG M, et al. Nucl Instr and Meth A, 2014, 756: 1. doi: 10.1016/j.nima.2014.04.051 [23] YAN X L, CHEN R J, WANG M, et al. Nucl Instr and Meth A, 2019, 931: 52. doi: 10.1016/j.nima.2019.03.058 [24] XING Y M, ZHANG Y H, WANG M, et al. Nucl Instr and Meth A, 2019, 941: 162331. doi: 10.1016/j.nima.2019.06.072 [25] TARASOV O, BAZIN D. Nucl Instr and Meth B, 2008, 266(19): 4657. doi: 10.1016/j.nimb.2008.05.110 [26] WANG M, HUANG W, KONDEV F, et al. Chin Phys C, 2021, 45(3): 030003. doi: 10.1088/1674-1137/abddaf [27] TU X L, WANG M, LITVINOV Y A, et al. Nucl Instr and Meth A, 2011, 654(1): 213. doi: 10.1016/j.nima.2011.07.018 [28] ZHANG Y H, ZHANG P, ZHOU X H, et al. Phys Rev C, 2018, 98: 014319. doi: 10.1103/PhysRevC.98.014319 [29] ZHANG M, ZHANG Y H, WANG M, et al. Nucl Instr and Meth A, 2022, 1027: 166329. doi: 10.1016/j.nima.2022.166329 [30] CHEN R J, YAN X L, GE W W, et al. Nucl Instr and Meth A, 2018, 898: 111. doi: 10.1016/j.nima.2018.04.056 [31] LIU J H, XU X, ZHANG P, et al. Nucl Instr and Meth B, 2020, 463: 138. doi: 10.1016/j.nimb.2019.06.007 [32] ZHANG P, XU X, SHUAI P, et al. Phys Lett B, 2017, 767: 20. doi: 10.1016/j.physletb.2017.01.039 [33] XU X, ZHANG P, SHUAI P, et al. Phys Rev Lett, 2016, 117: 182503. doi: 10.1103/PhysRevLett.117.182503 -











 下载:
下载:


















































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号