-
计算机模拟工具在反应堆工程领域有广泛的应用。近年来,国外发展的先进模拟与仿真技术依托高性能计算能力,以“第一性原理”的物理学为基础建立模型,取代经验公式,在虚拟世界中重建现实世界的实体与系统,实现对复杂系统的预测性模拟,已在材料研发、气候预测等领域取得了巨大进展与效益。核科学技术研究和核工程设计中,为了提高核设计的精确度,可从两方面入手:一方面是努力改进核设计的计算模型和计算方法,以提高计算的精确度;另一方面是提高核数据的精确性。对于核工程技术人员来讲,正确地了解和使用核数据是非常重要的,因为它是获得正确计算结果的前提和基础。
热中子反应堆设计计算使用的核材料截面,尤其是慢化剂材料的热中子散射数据对热中子反应堆的核设计和中子学分析、热中子过滤器、冷中子源设计等工作至关重要。热能区中子的散射截面不仅与中子的能量相关,还与发生散射介质的温度、物理和化学性质相关,强烈依赖材料本身的声子态密度的性质。以往的常用慢化剂材料的声子态密度大多数基于20世纪60年代的简化声子模型[1],在引入较多近似的条件下才能得到热中子散射数据,给反应堆临界和中子能谱计算引入了较大误差,近十年来国内外陆续基于第一性原理和分子动力学的理论进行了多种材料的热中子散射数据产生与计算方法的研究,并持续更新国际核评价数据库[2-5]。五大国际核数据评价库包括美国的ENDF /B、欧洲的JEFF、俄罗斯的BROND、日本的JENDL和中国的CENDL数据库,以美国的为例,早期的ENDF/B-VI.8 只有十五种热中子散射材料,ENDF/B-VII.0有二十种热中子散射材料, ENDF/B-VII.1扩充到二十一种热中子散射材料,最新的 ENDF/B-VIII.0更是提供了二十四种热化材料的三十四项热散射数据。同一材料不同结构的情况得到了有效处理,比如石墨,数据库就给出了三种不同孔隙率的热散射数据,扩充的这些热中子散射数据库大部分是基于第一性原理和分子动力学模拟得到的声子态密度完成的。热中子材料声子态密度的计算需要了解原子系统的动力学,这包括晶格结构和由声子色散关系和偏振矢量表示的振动类型,这种振动可以以声子态密度的形式表示,而传统的声子态密度是通过建立原子间相互作用的解析模型、评估原子间的力常数、构造动力学矩阵和对角化来计算的。动力矩阵计算中的力常数可以用不同的方法来估计,一般它们来自热力学性质,比如比热容或者压缩率数据;此外,还可以利用非弹性散射技术从声子色散关系的实验测量中推断出声子色散关系。这两种方法基本上都是半解析关系式和实验数据的拟合,有两个主要缺陷,第一,它不是可预测的,产生的原子力常数的色散关系是由实验数据推测的;第二,结果并不是唯一的,有可能被其他动力学模型替代。相比于半经验关系式产生声子态密度方法,第一性原理方法更贴近物理本质,无需拟合实验数据,它将多元素的原子体系当作由原子核和电子构成的多粒子体系,针对不同的晶格结构,基于量子力学的基本原理,在不引入任何实验参数的条件下对多原子体系进行处理,基于严格和准确的密度泛函理论,将固体抽象为具有平移周期性的理想晶体,认为原子围绕其平衡位置振荡,问题的求解归结为单电子在周期性势场中的运动的求解。利用第一性原理计算材料声子态密度,较之前凭借经验公式和简单的动力学模型的计算,具有明显的通用性,它允许了更复杂、更系统的多原子动力学模型,为热中子散射截面的计算奠定了重要的理论基础。
为满足热中子反应堆对热中子散射数据的迫切需求,针对目前热中子散射数据产生与处理技术面临的问题,本文将开展第一性原理的热中子散射截面计算研究。本文主要分为以下几个部分:第一部分简要概述热中子散射理论;第二部分介绍第一性原理Al和Bi金属热中子散射数据的计算方法和建模,第三部分给出Al和Bi金属热中子散射数据的计算结果并讨论分析;第四部分给出结论。
-
在热中子反应堆中,对于能量低于1 eV的中子,由于中子能量与散射核的热能是可比较的,不能简单认为靶核是静止的。这种情况下,中子很容易与物理离子发生非弹性碰撞,它们通过声子的湮灭与产生可以获得或者失去能量,通过热中子非弹性散射截面表示。同时,由于较低能量中子的德布罗意波长与物质分子或晶体内核的间距相差不大,与不同核发生散射的中子间可能发生干涉,即布拉格效应,通过相干弹性散射截面来表示[6]。热能区的中子散射截面不单纯是与中子能量有关,还与散射介质的温度及物理、化学性质有关,它反映的是材料自身的声子态密度特征,因此必须要研究散射物质的声子振动特性。
对非弹性散射截面,包括相干和非相干非弹性散射,对所有物质都重要,用热散射律表示。非弹性散射截面一般由其双微分散射截面推导而来[7]:
$$ {\sigma _{{\text{in}}}}(E,T) = \iint {\frac{{{{\rm{d}}^2}\sigma }}{{{\rm{d}}\Omega {\rm{d}}{E{'}}}}{\rm{d}}\Omega {\rm{d}}E'} \text{,} $$ (1) 其中:E和E΄是实验系中入射和散射中子的能量;
$ \Omega $ 是实验系下的散射角度;$ T $ 是温度,单位是eV。为了计算得到非弹性散射截面,一般利用NJOY程序的LEAPR模块和THERMR模块,NJOY程序的计算主要基于“不相干近似”[8],认为$$ \frac{{{{\rm{d}}^2}\sigma }}{{{\rm{d}}\Omega {\rm{d}}{E{'}}}} = \frac{1}{{4\pi }}\sqrt {\frac{{E'}}{E}} \left[ {{\sigma _{{{\rm{coh}}}}} + {\sigma _{{{\rm{inc}}}}}} \right]{S_{{\rm{s}}}}(\alpha ,\beta ) \text{,} $$ (2) 式中:
$ {\sigma _{{{\rm{coh}}}}} $ 是材料的束缚核的相干散射截面;${\sigma _{{{\rm{inc}}}}}$ 是材料的束缚核的非相干散射截面;α为动量转移量;β为能量转移量,表达式分别如下:$$ \alpha = \frac{{E' + E - 2\sqrt {E'E} \cos \theta }}{{AkT}} = \frac{{{\hbar ^2}{\kappa ^2}}}{{2MkT}} \text{,} $$ (3) $$ \beta = \frac{{E' - E}}{{kT}} = \frac{\varepsilon }{{kT}} \text{,} $$ (4) 其中:θ为入射和出射中子夹角;A表示散射核的原子质量M和中子质量的比值;
$ \kappa $ 为动量转移量;$ \varepsilon $ 为能量转移量,kT 是温度;单位是eV;$ \hbar $ 为普朗克常数;Ss(α, β)为不考虑相互作用的自散射律,可以写成:$$ {S_{{\rm{s}}}}(\alpha ,\beta ) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {{{\rm e}^{{\rm{i}}\beta t}}} {{\rm e}^{ - \gamma \left( t\right)}}{\rm{d}} t \text{,} $$ (5) 其中:
$t$ 是测量时间(秒),以$ \hbar /\left( {kT} \right) $ 为单位;$\gamma ( t)$ 表示为$$ \gamma \left( t\right) = \alpha \int_{ - \infty }^\infty {\frac{{\rho (\beta )}}{{2\beta \sinh (\beta /2)}}} \left[1 - {{\rm e}^{ - {\rm{i}}\beta t}}\right]{{\rm e}^{ - \beta /2}}{\rm{d}}\beta \text{,} $$ (6) 其中的
$ \rho (\beta ) $ 是以$ \beta $ 为单位的声子态密度,并且是归一化的,也是NJOY程序唯一需要输入的外部量,是本文采用第一性原理计算的重要输出值,声子态密度的结果直接影响热中子散射数据的质量和准确度。当
$ \alpha $ 和$ \left| \beta \right| $ 值较大时($ \alpha \geqslant {\alpha _{sw}},\left| \beta \right| \geqslant {\beta _{sw}} $ ),即在较高的入射能量的时候,$ \alpha $ 和$ \beta $ 已经超出了$ S(\alpha ,\beta ) $ 范围,这时就需要引入短时间碰撞近似(SCT),热中子的非弹性散射表达如下所示[9]:$$ {S^{{\rm{SCT}}}}(\alpha ,\beta ,T) = \frac{{{{\rm{e}}^{ - \left[\tfrac{{{{\left(\alpha - \left| \beta \right|\right)}^2}T}}{{4\alpha {T_{{\rm{eff}}}}(T)}} + \tfrac{{\left| \beta \right|}}{2}\right]}}}}{{\sqrt {4\pi \alpha \dfrac{{{T_{{\rm{eff}}}}(T)}}{T}} }} \text{,} $$ (7) 其中有效温度是由声子谱计算得到的:
$$ {T_{{\rm{eff}}}} = \frac{1}{2}\int\nolimits_0^{\,{\omega _{\max }}} {\hbar \omega \coth \left( {\frac{{\hbar \omega }}{{2kT}}} \right)} \rho (\omega ){\rm{d}}\omega \text{,} $$ (8) 进而得到“短时间碰撞下”的双微分截面为
$$ \begin{split} {\sigma ^{{\rm{SCT}}}}(E,E',\mu ) = & \frac{{{\sigma _{\rm{b}}}}}{{2kT}}\frac{{\sqrt {E'/E} }}{{\sqrt {4\pi \alpha {T_{{\rm{eff}}}}/T} }}\times\\ &\exp \left\{ { - \frac{{{{(\alpha - \left| \beta \right|)}^2}}}{{4\alpha }}\frac{T}{{{T_{{\rm{eff}}}}}} - \frac{{\beta + \left| \beta \right|}}{2}} \right\} \text{,} \end{split}$$ (9) 其中
$ {\sigma _{\rm{b}}} $ 为束缚核的总散射截面。对于由相干散射体组成的物质中,零声子项给出了相干散射函数,对应的相干散射截面为$$ {\sigma _{\rm{coh}}}(E,\mu ) = \frac{{{\sigma _{{\rm{c}}}}}}{E}\sum\limits_{{E_i} < E} {{f_i}{{\rm e}^{ - 4W{E_i}}}\delta (\mu - {\mu _i})} \text{,} $$ (10) 其中:
$ {\sigma _{{\rm{c}}}} $ 为束缚核的相干散射截面;$ \mu $ 是散射角余弦;W是德拜沃积分;$ {f_i} $ 是跟晶格结构因子有关的一个系数:$$ {f_i} = \frac{{2\pi {\hbar ^2}}}{{4mNV}}{\sum\limits_{{\tau _i}} {\left| {F(\tau )} \right|} ^2} \text{;} $$ (11) $ F(\tau ) $ 是每个原子的相位,表达式如下:$$ {\left| {F(\tau )} \right|^2} = {\left| {\sum\limits_{{\tau _i}} {{{\rm e}^{{\rm i}2\pi \phi j}}} } \right|^2} \text{。} $$ (12) 对式(10)进行角度和能量的积分,得:
$$ {\sigma _{\rm{coh}}} = \frac{{{\sigma _{{\rm{c}}}}}}{E}\sum\limits_{{E_i} < E} {{f_i}{e^{ - 4W{E_i}}}} \text{,} $$ (13) $$ {E_i} = \frac{{{\hbar ^2}{\tau _i}^2}}{{8m}} \text{,} $$ (14) 其中:
$ {\tau _i} $ 是倒格子壳矢量长度;m是中子质量。不同晶格结构晶体的结构因子计算是不同的,NJOY的LEAPR模块中仅内置了面心立方FCC(Face-Centred Cubic)、体心立方BCC(Body-Centred Cubic)和六角形HCP(Hexagonal Close Packed)的结构,对于其他与内置结构不符的结构就需要用户自己输入结构因子,并重新编译LEAPR模块,比如对于Bi金属的相干弹性散射,Bi金属属于菱方晶系,单元晶胞中含有两个原子,菱晶角度为57.23°,在298.0 K温度下Bi原子的位置参数z = 0.227 1,倒格子壳矢量可以表示为
$$ {\boldsymbol{\tau}} = {l_1}{{\boldsymbol{b}}_1} + {l_2}{{\boldsymbol{b}}_2} + {l_3}{{\boldsymbol{b}}_3} \text{,} $$ (15) 其中
$ {l_1} $ ,$ {l_2} $ ,$ {l_3} $ 是晶面指数,为表征晶胞位置的参数,$ {\boldsymbol{b}}_{1} $ ,$ {\boldsymbol{b}}_{2} $ ,$ {\boldsymbol{b}}_{3} $ 是坐标矢量,表达式如下$$ \begin{gathered} {{\boldsymbol{b}}_1} = 2\pi \frac{{{a_2} \times {a_3}}}{{{a_1} \cdot {a_2} \times {a_3}}} = 2\pi \left(\frac{1}{{{a_{{\rm{H}}}}}}{\boldsymbol{x}} - \frac{1}{{\sqrt 3 {a_{{\rm{H}}}}}}{\boldsymbol{y}} + \frac{1}{{{c_{{\rm{H}}}}}}{\boldsymbol{z}}\right), \\ {{\boldsymbol{b}}_2} = 2\pi \frac{{{a_3} \times {a_1}}}{{{a_1} \cdot {a_2} \times {a_3}}} = 2\pi \left(\frac{2}{{\sqrt 3 {a_{{\rm{H}}}}}}{\boldsymbol{y}} + \frac{1}{{{c_{{\rm{H}}}}}}{\boldsymbol{z}}\right), \\ {{\boldsymbol{b}}_3} = 2\pi \frac{{{a_1} \times {a_2}}}{{{a_1} \cdot {a_2} \times {a_3}}} = 2\pi \left( - \frac{1}{{{a_{{\rm{H}}}}}}{\boldsymbol{x}} - \frac{1}{{\sqrt 3 {a_{{\rm{H}}}}}}{\boldsymbol{y}} + \frac{1}{{{c_{{\rm{H}}}}}}{\boldsymbol{z}}\right), \\ \end{gathered} $$ (16) $ {a_{{\rm{H}}}} $ ,$ {c_{{\rm{H}}}} $ 为对应六角形坐标系中Bi的晶胞参数,${a_{{\rm{H}}}} = 4.557\,\mathop {\rm A}\limits^ \circ$ ,${c_{{\rm{H}}}} = 11.862\,\mathop {\rm A}\limits^ \circ$ ,原胞结构包含两个Bi原子,分别位于坐标(Z, Z, Z)和(−Z, −Z, −Z)处。由式(12),可以得到Bi的晶格结构因子:$$ \left| {F(\tau )} \right| = {\left| {{{\rm e}^{{\rm i}2\pi z({l_1} + {l_2} + {l_3})}} + {{\rm e}^{ - {\rm i}2\pi z({l_1} + {l_2} + {l_3})}}} \right|^2} = 4{\cos ^2}\big[ {2\pi z({l_1} + {l_2} + {l_3})} \big] \text{。} $$ (17) -
本文首先研究了第一性原理声子态密度的产生方法,可以分为两类,第一类为直接计算法,根据畸变晶格和理想晶格的能量差来计算出位移振幅函数,进而通过移位原子得到力学矩阵,计算出声子态密度,称为冷冻声子法;第二种方法为间接方法,通过描述价电子密度对周期晶格的扰动响应得到声子态密度结果,称为密度泛函微扰理论法。常用的软件有CASTEP程序[10]、VASP程序[11]、PHONON程序和PHONONPY程序[12],其中VASP和商业程序PHONON的求解是采用的冷冻声子(Frozen Phonon, FP)直接法[12],而CASTEP采用的是基于密度泛函微扰理论的方法,简称DFPT(Density Function Perturbation Therory)方法[10],本文采用VASP程序结合开源程序PHONONPY通过脚本的方式既可以采用FP法又可以基于DFPT方法。
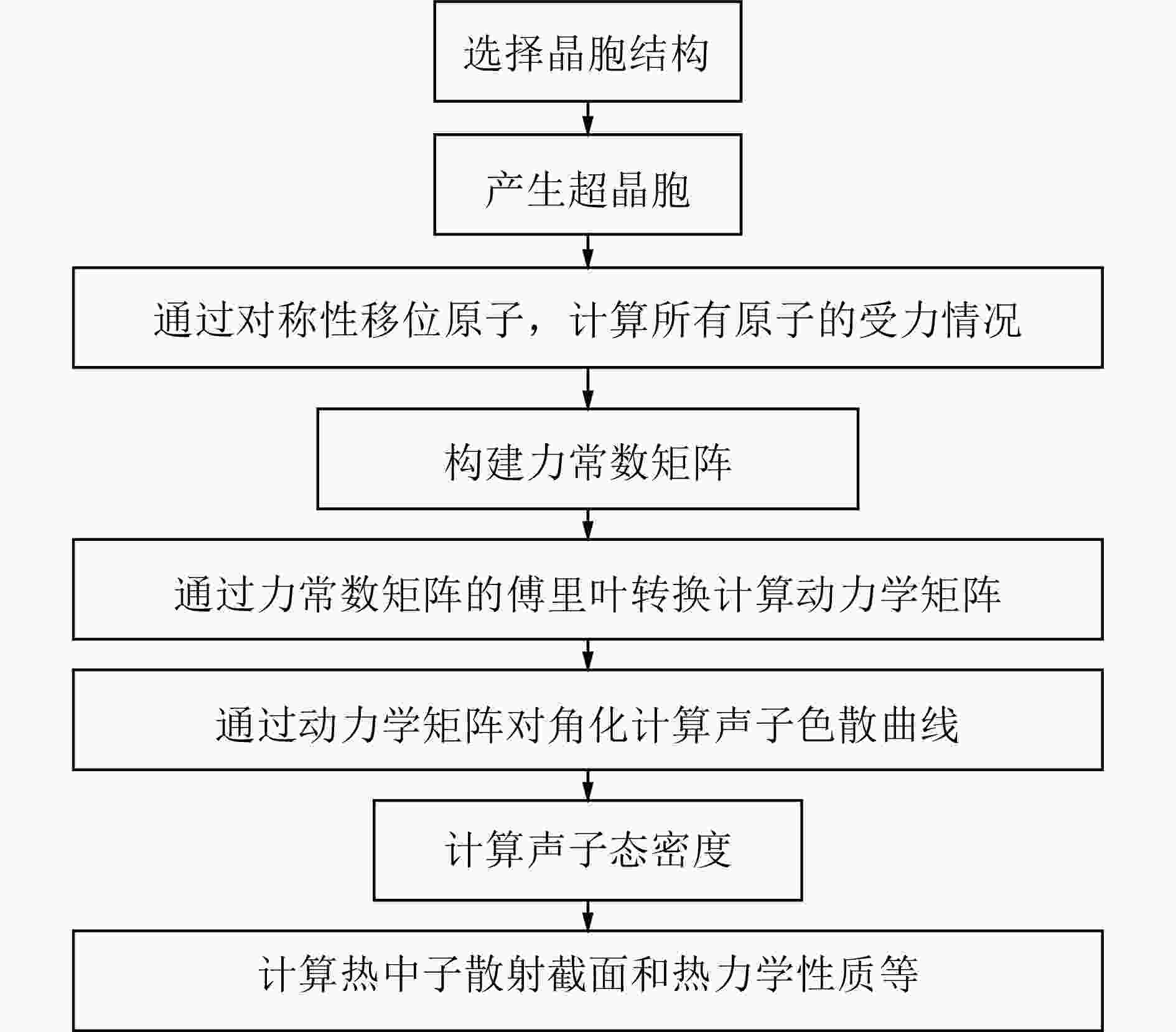
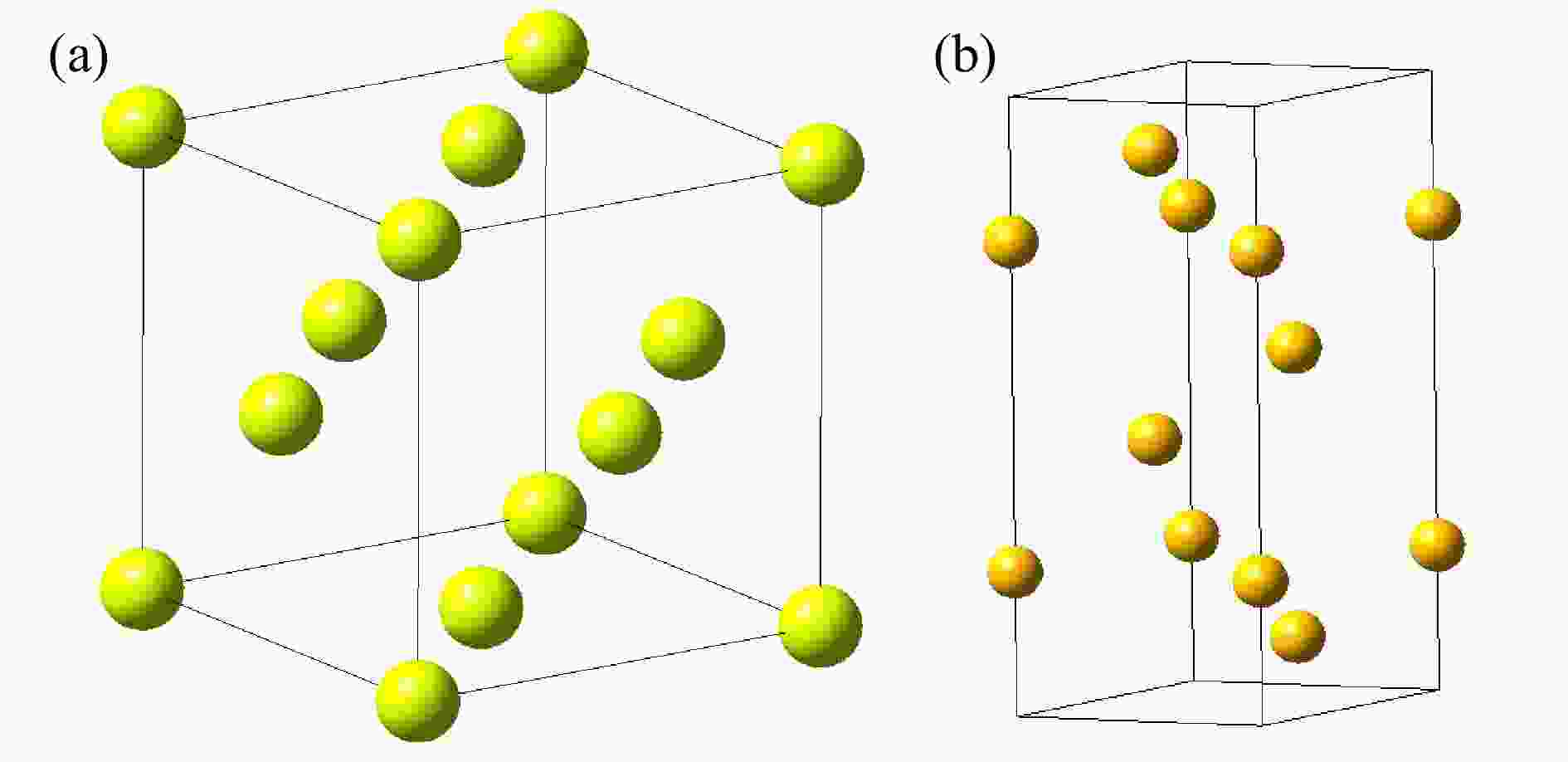
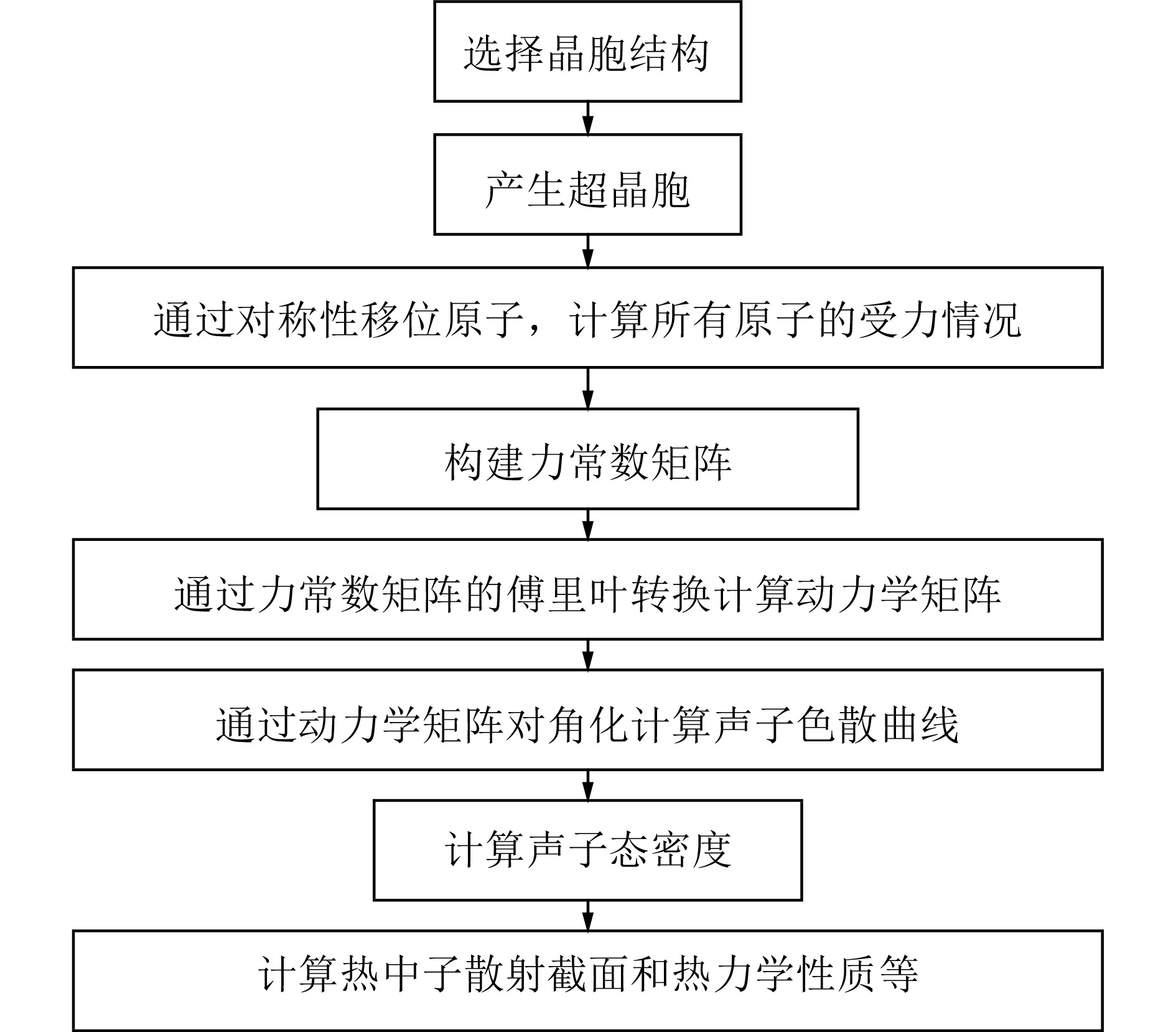
图1为第一性原理冷冻声子FP法计算声子态密度的流程图,首先选择要计算的晶胞,产生它的超晶胞组成结构,通过对称性移位原子,计算所有原子的受力情况,构建力常数矩阵,通过力常数矩阵的傅里叶变换得到动力学矩阵,再通过动力学矩阵对角化计算材料的声子色散曲线,分析材料的声子色散曲线,得到材料的声子态密度,利用得到的声子态密度就可以得到材料的热中子散射数据和相关的热力学性能参数。它是一种直接的方法,基于原子从平衡位置位移的总能量变化或力计算的方法,只要原子的受力可以导出,就可以根据力学常数矩阵得到相应的声子态密度,但是该方法的缺点是必须要考虑超级晶胞,这对于单元与单元之间扩展较小的简单晶体结构是不太适用的。而密度泛函微扰理论DFPT法为间接计算法,它是对平衡晶格几何进行扰动后,通过微扰理论分析计算得到力常数的解析方法。DFPT不同于冷冻声子方法,其主要的原理是通过计算晶体对外界的能量变化的响应从而计算晶体的动力学性质,该方法不用扩胞,也不需要波矢正交与晶胞边界,DFPT为复杂晶体的晶格动力学分析提供了有力的计算手段,被认为是相当精确、有效和可靠的方法。然而,它需要高度专业化的第一性原理计算程序,并且还需要基于原始程序对其进行相关的改动和补充,这也是本文采用开源程序PHONONPY的初衷。本文将分别对比这两种方法在晶体Al和Bi声子态密度计算中的差异,晶体Al和Bi的晶格结构如图2所示,其中Al属于典型的面心立方结构,Bi属于菱方晶系。
在NJOY制作热散射律的过程中需要注意一些操作细节。图3为NJOY制作ACE各式的热中子散射律数据库的具体步骤,其中,MODER模块是将ENDF/B库中原始的核素数据库进行十进制到二进制的转换,因为计算机便于运行二进制文件,然后RECONR模块对原始核素库的截面数据进行共振重造,重建误差设为0.001,紧接着BROADR模块对其进行多普勒展宽,薄化误差设为0.001,然后将加工后的快中子数据提供给THERMR模块,与此同时,LEAPR模块将加工好的ENDF/B格式的热中子散射律数据给THERMR模块,THERMR模块负责热区散射矩阵等的计算,然后将生成的点截面库PENDF格式的数据库送给ACER模块,制作成MCNP软件的ACE格式的数据库。ACER模块最后生成两个数据文件:一个是新制的MCNP中子截面库文件,放到MCNP截面库文件夹内;另一个是路径文件,用来添加到MCNP软件的索引文件XSDIR里面,以供MCNP程序计算时调用相应截面库。整个流程中最重要的是LEAPR模块和THERMR模块,多普勒展宽等对其影响很小,主要是为了提供一些基本的散射截面等数据,而热区中子在核素内的散射情况由LEAPR模块的散射律数据决定。
目前NJOY在制作热散射律过程中,常见慢化剂材料的MAT号和相关的反应道MT参照早期ENDF/B VI格式的数据库定义的材料及热截面号码,然而,早期ENDF/B VI格式的数据库对慢化剂材料的定义不是很完善,只对常用慢化剂材料进行了研究,导致NJOY对新型慢化材料的识别(MAT号码)还有限制,本文参照ENDF/B VI现有格式的规则,针对Al和Bi,重新定义热中子散射律的MAT号和热截面MT号码,以供NJOY的LEAPR和THERMR使用。
除了材料本身的声子态密度,NJOY程序还需要输入材料的束缚核截面等基本参数。表1列出了Al和Bi束缚核的质量数A及不同反应截面的值,包括吸收截面
$ {\sigma _{{\text{ab}}}} $ ,相干散射截面$ {\sigma _{{\text{coh}}}} $ ,不相干散射截面$ {\sigma _{{\text{inc}}}} $ ,束缚核总截面$ {\sigma _{\text{b}}} $ ,自由气体截面$ {\sigma _{{\text{free}}}} $ 。可以看出,对于Al和Bi这种金属晶体,相干弹性散射是比较严重的,Al是FCC结构,NJOY程序中内置了相干散射计算功能,但Bi计算时需要重新构置晶格学结构因子,并且添加到THERMR模块中。表 1 Al和Bi核的不同反应的束缚截面
单位:b 原子 A $ {\sigma _{{\text{ab}}}} $ $ {\sigma _{{\text{coh}}}} $ $ {\sigma _{{\text{inc}}}} $ $ {\sigma _{\text{b}}} $ $ {\sigma _{{\text{free}}}} $ 27Al 26.75 0.231 0 1.495 0.008 2 1.503 1.396 6 209Bi 207.2 0.033 8 9.148 0.008 4 9.156 9.068 3 -
本文采用VASP进行Al和Bi的几何结构优化,选取Pearson数据库中的实验值作为几何优化的初始参数,模拟晶格参数和原子位置,分别选取广义梯度近似GGA和局域密度泛函LDA的赝势,利用VASP程序包中的结构优化选项将结构松弛到它的最低能量状态,初始参数选取Pearson数据库中的实验值,对晶格参数和原子位置进行模拟,电子能量收敛标准选取1×10−5 eV,平面波截断能为400 eV,计算结果如表2所列。从结果中可以看出,与局域密度泛函LDA相比,广义梯度近似GGA方法优化得到的晶格参数更接近Pearson数据库中的实验值。接下来,本文有关Al和Bi声子态密度的计算就采用GGA赝势优化得到的结构进行。
表 2 Al和Bi晶格参数的对比
材料 方法 GGA LDA Pearson数据库 值 误差/% 值 误差/% Al a = b = c 4.05 0.2 4.00 −1.2 4.04 Bi a 4.57 0.4 4.50 1.1 4.56 c 11.90 0.4 11.52 2.9 11.86 -
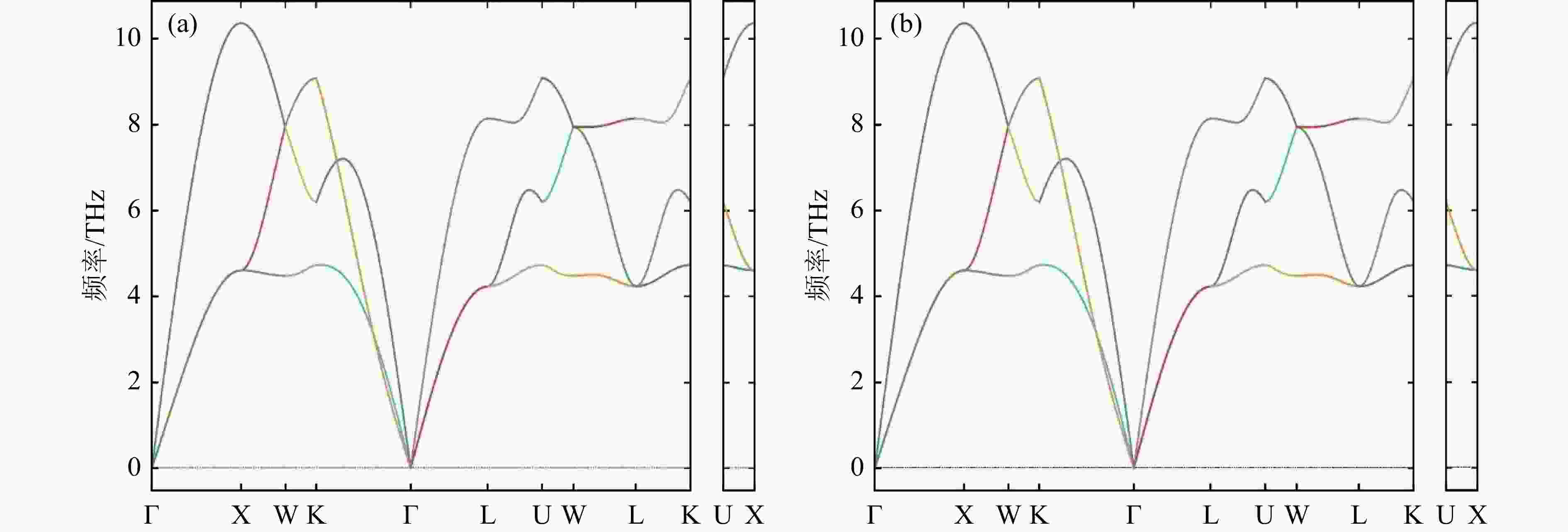
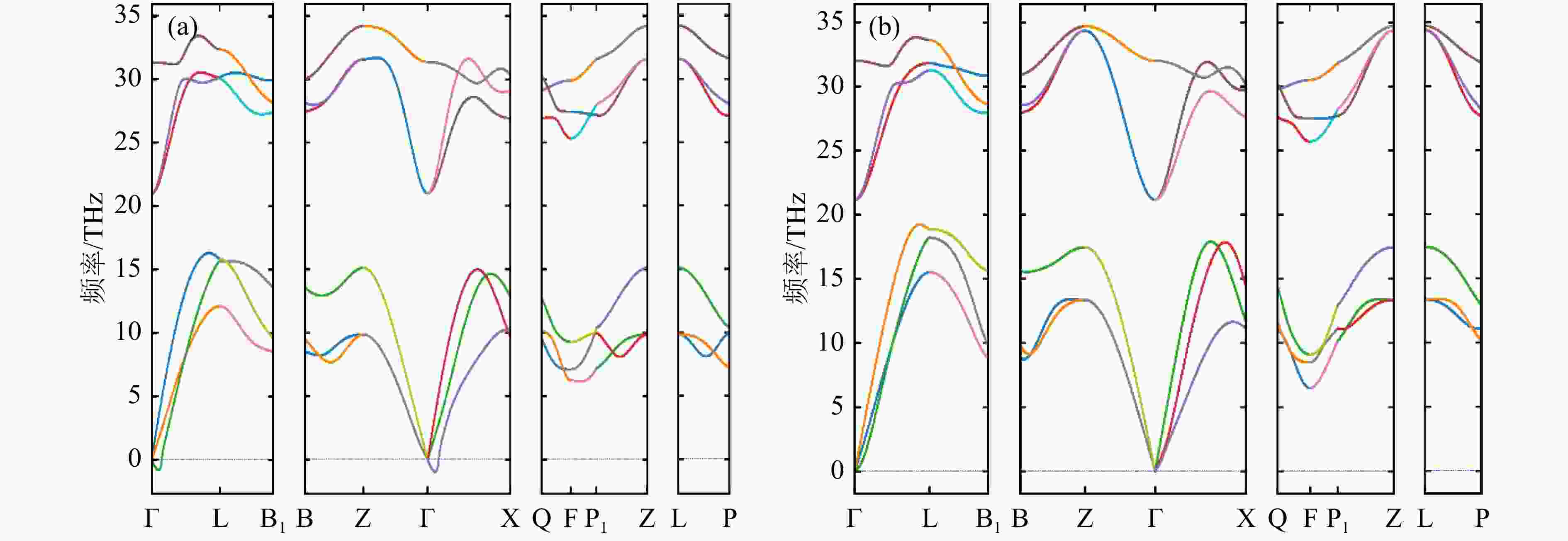
采用优化好的Al和Bi的晶格结构,本文利用了灵活性更强的PHONONPY开源软件结合VASP软件计算了Al和Bi的声子态密度,交换关联函数使用GGA-PBE,截断能量最终选取为400 eV,计算采用周期性超晶格方法,超晶胞大小为4 × 4 × 4,Al和Bi的布里渊区积分在3 × 3 × 3的K网格Monkhost-Pack格子中进行,本文分别采用了FP法和DFPT法计算了Al和Bi的声子色散关系,利用冷冻声子FP法和密度泛函微扰理论DFPT法得到Al声子色散关系在布里渊区不同方向的计算结果如图4、图5所示,较低的分支为声学项,较高的分支为光学项。从图中可以看出,对于Al晶体而言,DFPT和FP结果基本类似,均可以用来产生合理的声子态密度,进而得到热中子散射数据,对Bi晶体,用FP方法得到的色散关系在伽马点周围包含一些虚频,这可能是因为采用的超晶胞不够大或者原胞结构的原子弛豫不够,计算中要避免采用有虚频的结果, DFPT法得到的Bi色散曲线结果并没有虚频,下面将采用DFPT法的Bi声子计算结果进行热中子散射数据的研究。
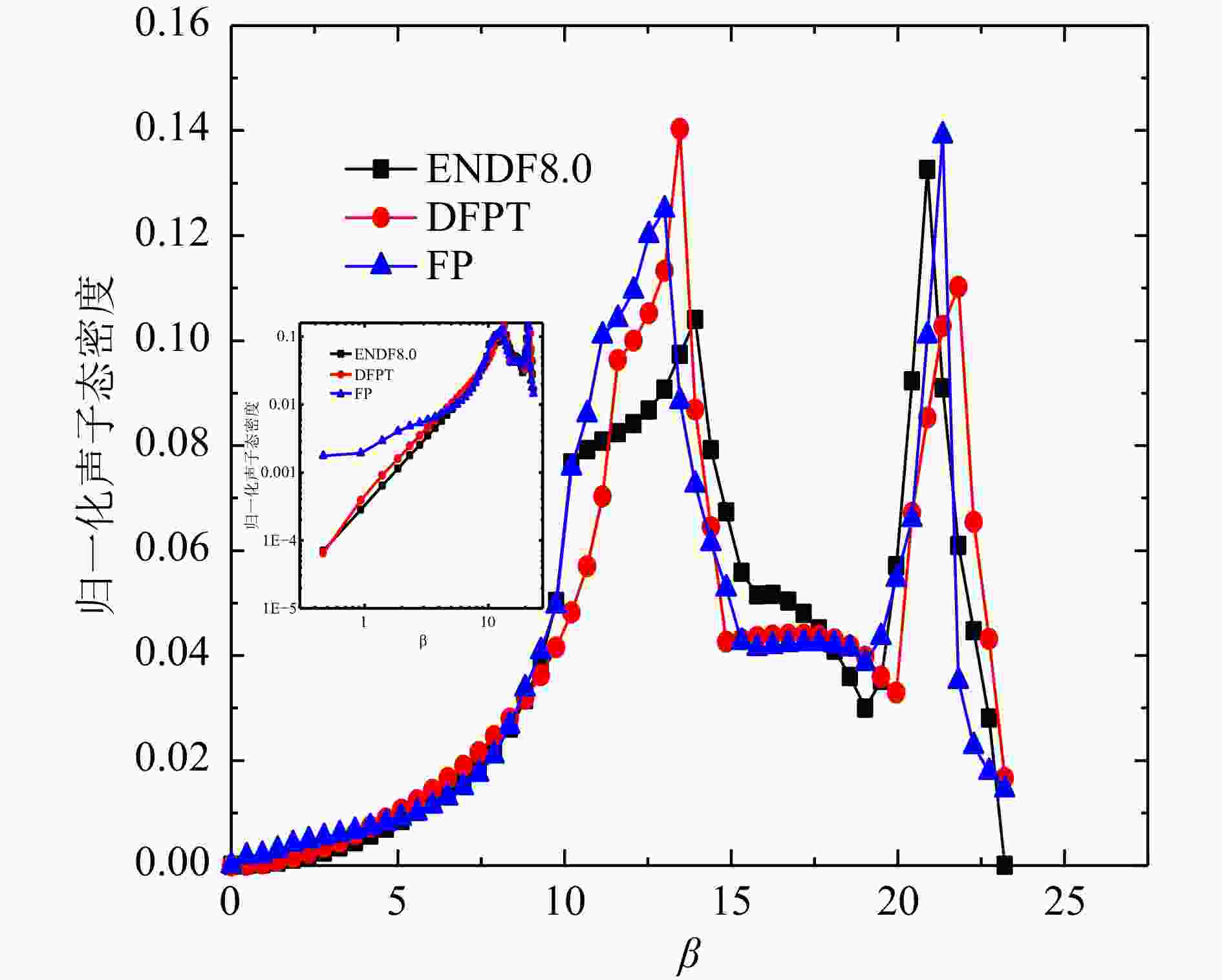
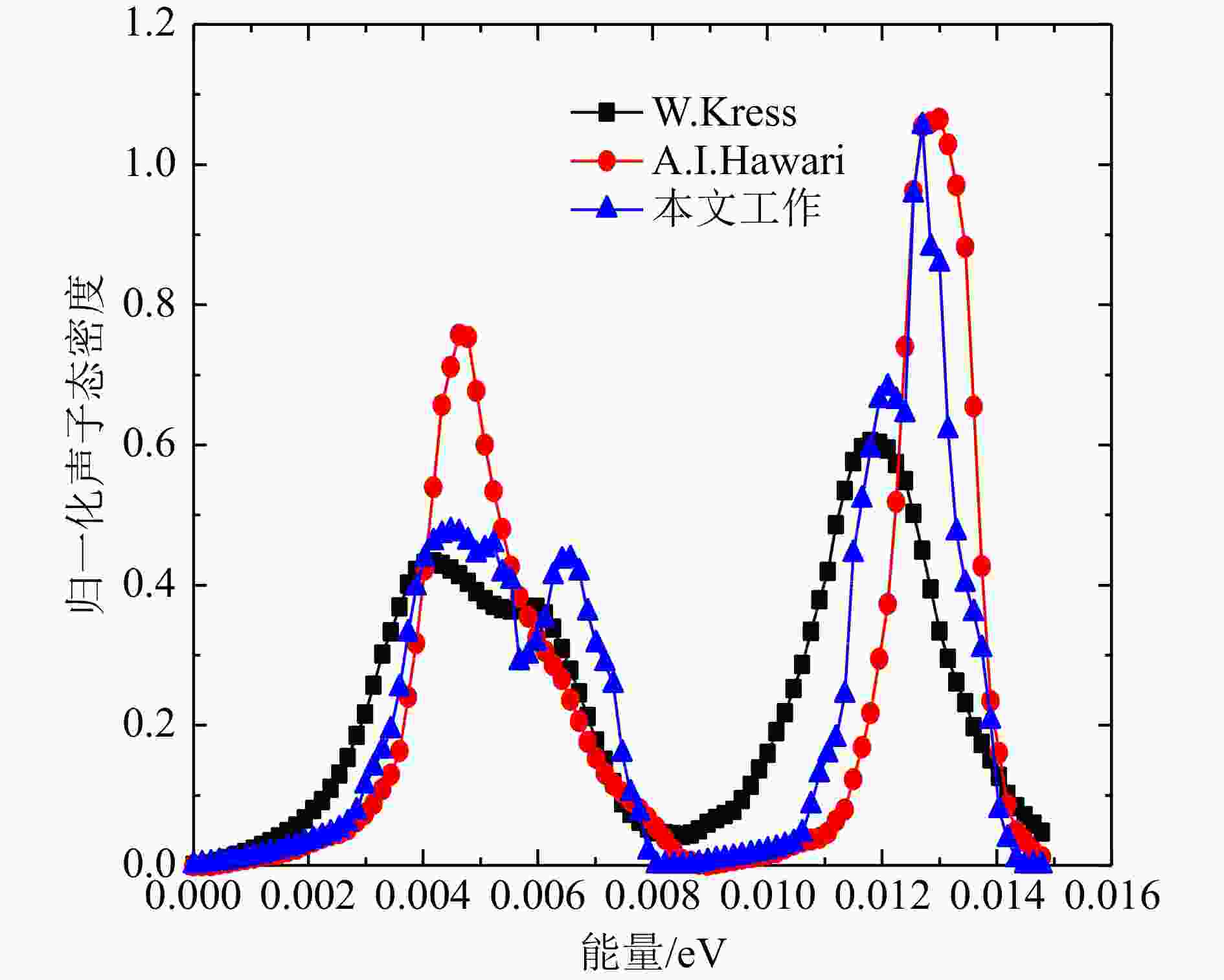
Al和Bi得到的声子态密度计算结果与文献对比如图6、图7所示。 由于ENDF8.0和FP法、DFPT法结果的声子态密度单位不统一,本文选取了β网格下的归一化的声子态密度进行对比,Al原子的FP法和DFPT法,以及ENDF8.0的声子态密度中数据基本趋势一致。从对数图的结果可以看出,低能区DFPT和ENDF8.0的符合更好,相较于Al原子,Bi的声学项和光学项分隔明显,计算值在0.008~0.009 eV区间态密度值为零,这主要归因于Bi的结构与简单的立方晶格的差异,本文Bi的DFPT计算结果相较于Hawari的计算在声学项上更接近W. Kress的实验声子态密度[13],光学项与Hawari的结果基本一致,但峰值数据偏低,并且有更小的展宽,两个计算值与实验值均稍微有偏差,出现偏差的原因可能是计算中原胞结构的原子弛豫不够以及实验本身测量的误差,整体来看,DFPT法的声子态密度产生方法更灵活和可靠。
-
分别基于FP法和DFPT法得到的Al声子态密度,利用NJOY完成了Al晶体不同下声子态密度模型热中子散射截面的对比,如图8所示。从图8(a)可以看出,FP的声子态密度得到的Al不相干非弹性散射截面比DFPT声子态密度结果偏高,DFPT模拟结果与ENDF8.0的结果更接近,主要差异体现在10−9~10−7 MeV之间。从图8(b)可以看出,相较于FP法,采用DFPT法得到的声子态密度与ENDF8.0不相干非弹性散射截面和相干弹性散射截面符合较好,并且随着能量的增加,FP法与DFPT法的截面差异越大,而DFPT法和ENDF8.0基本一致,说明DFPT法的声子态密度与ENDF8.0采用的声子态密度在热中子散射特性上更匹配。
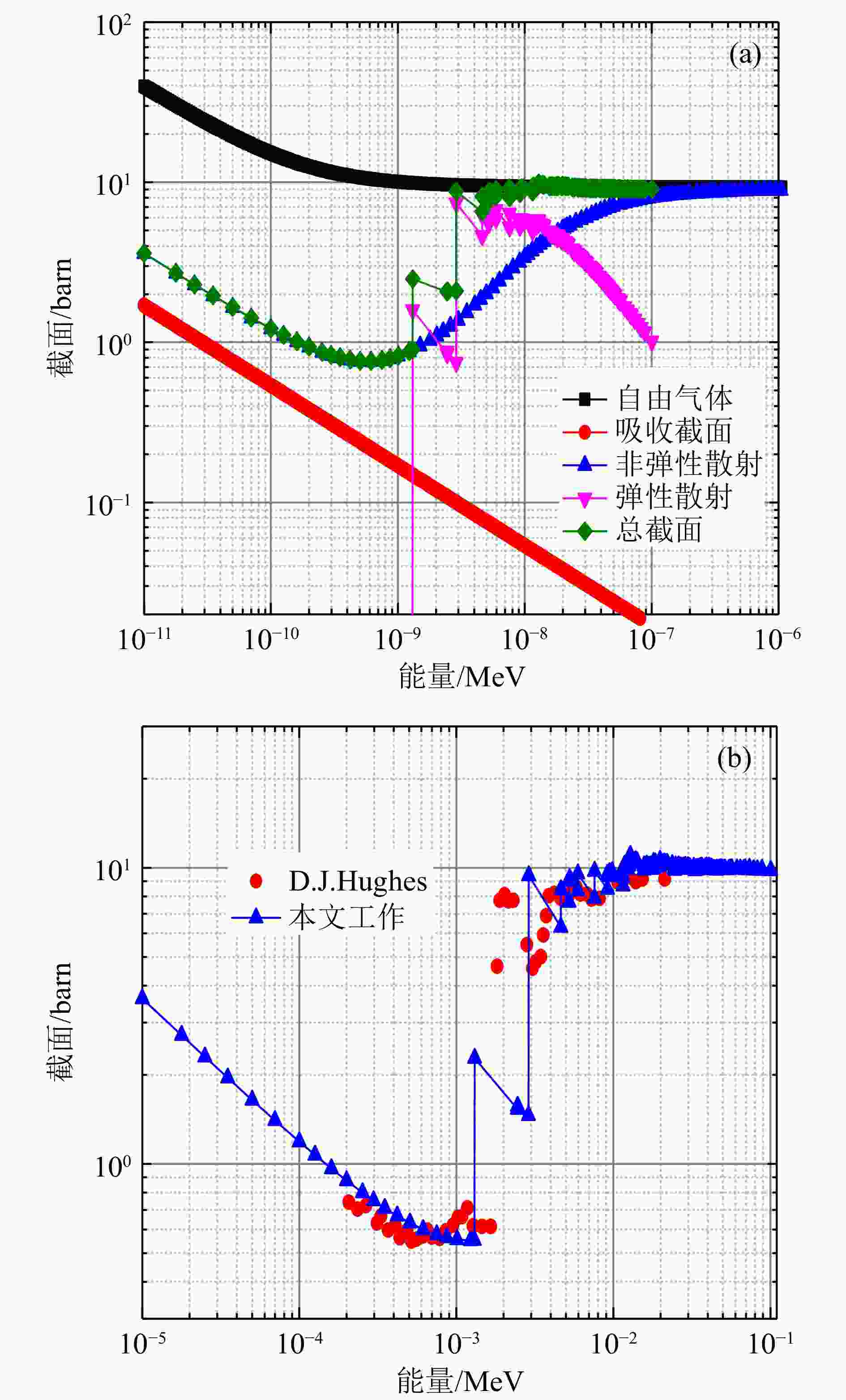
考虑到Bi的FP声子色散关系有虚频,本文采用DFPT法得到的Bi声子态密度计算了Bi原子300 K下热中子散射截面。由于目前国际公开核数据库中均没有Bi的热中子散射数据,因此本文将计算值与自由气体模型和实验值[14]进行了比较,如图9所示。从图9(a)可以看出,Bi原子自由气体模型在低能时,特别是能量在布拉格阈值以下,大大高估了Bi原子的中子总截面值,这时总截面主要是非弹性散射截面的贡献,如果单纯使用自由气体模型将会使得最终的结果与实际的误差比较大,热中子过滤器Bi对热中子的过滤效果没有体现出来。从图9(b)可以看出,本文的计算结果与实验值较为一致,能明显体现出Bi特定阈值下的布拉格效应,同时也能看出,在布拉格阈值以下,本文计算的非弹性散射截面与实验值也符合较好。因此,本文从实际需要出发,研究Bi的热化效应是有必要的。
-
本文以Al和Bi金属的热中子截面制作为例,分别基于冷冻声子FP法和密度泛函微扰理论DFPT法,采用VASP结合PHONONY程序计算了它们的声子色散关系和声子态密度,基于NJOY程序,在LEAPR中添加Bi相干散射处理,完成了Al和Bi的热中子散射截面库制作。结果表明:对于Al,相较于FP法,DFPT法的声子态密度得到的热中子散射截面与ENDF8.0符合更好;对于Bi,采用DFPT法消除了FP法的虚频现象,得到的热中子散射结果与实验值符合较好。本文从探索材料内部特征机理的角度提出了一种更基础、更有预见性的制作热中子截面的方法,为研究新型反应堆的核材料热化机理奠定了理论基础。
Application of First Principles in Calculation of Thermal Neutron Scattering Cross Section
-
摘要: 第一性原理被应用在核工程领域关注的热中子散射材料的热中子截面计算中。本工作以Al和Bi金属的热中子截面制作为例,分别基于第一性原理冷冻声子法和密度泛函微扰法,采用VASP结合PHONONY程序计算了它们的声子色散关系和声子态密度。基于NJOY程序,在LEAPR中添加Bi相干散射处理,制作了Al和Bi的热中子散射截面库。结果表明:对于Al,相较于冷冻声子法,密度泛函微扰理论的声子态密度得到的热中子散射截面与ENDF8.0符合更好,对于Bi,采用密度泛函微扰法消除了冷冻声子法的虚频现象,得到的热中子散射结果与实验值符合较好。本工作从探索材料内部特征机理的角度提出了一种更基础、更有预见性的制作热中子截面的方法,为研究新型反应堆的核材料热化机理奠定了理论基础。Abstract: The calculation of thermal neutron cross section for thermal neutron scattering materials in the field of nuclear engineering is based on the first principle. This study utilizes Al and Bi metals as examples for the determination of thermal neutron cross sections. The frozen phonon method and density functional perturbation method are applied to calculate the thermal neutron cross sections for Al and Bi, respectively. Phonon dispersion relation and phonon density of state are computed using VASP and PHONONY. Subsequently, coherent scattering for Bi is incorporated into LEAPR using NJOY to generate the thermal neutron scattering cross-section libraries for Al and Bi. The results reveal that, in the case of Al, the thermal neutron scattering cross section obtained using the density functional perturbation theory is in better agreement with ENDF8.0 compared to the frozen phonon method. Conversely, for Bi, the density functional perturbation method eliminates the imaginary frequency phenomenon observed in the frozen phonon method, resulting in thermal neutron scattering results that align well with experimental data. The paper proposes a more fundamental and predictable method for generating thermal neutron cross-sections by exploring the internal characteristic mechanism of the material, thus laying a theoretical foundation for studying the thermal mechanisms of new reactor nuclear materials..
-
表 1 Al和Bi核的不同反应的束缚截面
单位:b 原子 A $ {\sigma _{{\text{ab}}}} $ $ {\sigma _{{\text{coh}}}} $ $ {\sigma _{{\text{inc}}}} $ $ {\sigma _{\text{b}}} $ $ {\sigma _{{\text{free}}}} $ 27Al 26.75 0.231 0 1.495 0.008 2 1.503 1.396 6 209Bi 207.2 0.033 8 9.148 0.008 4 9.156 9.068 3 表 2 Al和Bi晶格参数的对比
材料 方法 GGA LDA Pearson数据库 值 误差/% 值 误差/% Al a = b = c 4.05 0.2 4.00 −1.2 4.04 Bi a 4.57 0.4 4.50 1.1 4.56 c 11.90 0.4 11.52 2.9 11.86 -
[1] BEYSTER J R, BROWN, J R, CORNGOLD N. Integral Neutron Thermalization GA-9036 [R]. San Diego, Calif: John Jay Hopkins Lab. for Pure and Applied Science, 1963. [2] HAWARI A I, QASIR I I, GILLETTE V H, et al. Ab Initio Generation of Thermal Neutron Scattering Cross Sections[C]//Proceedings of Physor, April 25–29, 2004, Pennsylvania State University, Pennsylvania. 2004. [3] 王立鹏, 江新标, 吴宏春, 等. 物理学报, 2018, 67(20): 202801. doi: 10.7498/aps.67.20180834 WANG L P, JIANG X B, WU H C, et al. Acta Physica Sinica, 2018, 67(20): 202801. (in Chinese) doi: 10.7498/aps.67.20180834 [4] 王佳, 胡泽华, 宋红州, 等. 核动力工程, 2018, 39(1): 34. WANG J, HU Z H, SONG H Z, et al. Nuclear Power Engineering, 2018, 39(1): 34. (in Chinese) [5] BROWN D A, CHADWICK M B, CAPOTE R, et al. Nuclear Data Sheets, 2018, 148: 1. doi: 10.1016/J.NDS.2018.02.001 [6] BELL G I, GASSTONE S. Nuclear Reactor Theory[M]. New York: Van Nostrand, 1970. [7] MACFARLANE R E. New Thermal Neutron Scattering Files for ENDF/B-VI, Release 2[R]. Los Alamos: LANL, 1994. [8] MACFARLANE R E, MUIR D W, New Thermal Neutron Scattering Files for ENDF/B-VI, Release 2[R]. Los Alamos: LANL, 1994. [9] MATTES M, KEINERT J. Thermal Neutron Scattering Data for the Moderator Materials H2O, D2O and ZrHx in ENDF-6 Format and as ACE Library for MCNP(X) Codes[R]. Vienna: IAEA, 2005. [10] SEGALL M D, LINDAN P, PROBET M J, et al. Journal of Physics: Condensed Matter, 2022, 14(11): 2717. doi: 10.1088/0953-8984/14/11/301 [11] KRESSE G, FURTHMULLER J. Vienna Ab-Initio Simulation Package; VASP the Guide[R]. Vienna: IAEA, 2002. [12] CHAPUT L, TOGO A, TANAKA I, et al. Phys Rev B, 2011, 84: 094302. doi: 10.1103/PhysRevB.84.094302 [13] KRESS W. Phonon Dispersion Curves, One-phonon Densities of States and Impurity Vibrations of Metallic Systems[M]. Karlsruhe: Fachinformationszentrum, 1987. [14] HUGHES D J, HARVEY J A. Neutron Cross Sections[R]. Washington D C: Brookhaven National Laboratory Report 325, 1955. -




 下载:
下载:



























































 甘公网安备 62010202000723号
甘公网安备 62010202000723号