Exactly solvable models have played a fundamental role in understanding the physics of strongly correlated quantum systems in condensed matter and nuclear physics. In nuclear physics, an exactly solvable model typically describes the dynamics of a particular nuclear shape phase by writing the Hamiltonian as a linear combination of the Casimir operators of subgroups in a group chain. Elliott showed that the nuclear shell model(SM) admits SU(3) symmetry, generating the collective rotational spectra of deformed nuclei^[1-2]. Additionally, the U(6) interacting boson model provides a good description of rotational nuclei in the SU(3) limit, vibrational nuclei in the U(5) limit, and gamma-unstable nuclei in the O(6) limit^[3–5]. These exactly solvable situations have been valuable in providing benchmarks for describing the complex collective phenomena that arise in nuclear systems.

Pairing correlation is a dominant residual correlation in atomic nuclei that plays a crucial role in describing ground-state properties, electromagnetic transition rates, moments of inertia^[6–8], nuclear reactions^[9], and particle decay^[10]. The Richardson-Gaudin method, based on the SU(2) quasi-spin symmetry, was first proposed by Richardson and provides a solvable pairing model^[11-12]. Compared to exact diagonalization, the Richardson-Gaudin model has no dimension limitation^[13-14]. Recently, the exactly solvable pairing model has been used to investigate fission barriers and static fission paths in Th, U, and Pu isotopes, with the new iterative algorithm^[15-16] indicating that the impact of the pairing correlation differs during the fission process^[17]. The calculated barrier heights of even-even nuclei in Th, U, and Pu isotopes show that the exactly solvable pairing model provides a better description of the corresponding experimental barrier heights than the BCS scheme, confirming that it can describe the static and dynamic properties of fissioning systems.

The main objective of this paper is to systematically analyze the fission barriers of Th, Pa, U, Np, Pu, Am, Cm, Bk, and Cf isotope chains within the exactly solvable pairing model, using the efficient new iterative algorithm^[15-16]. We investigate the effect of the pairing interaction strength on the fission barrier heights of the nuclei considered.

The Hamiltonian of the exactly solvable pairing model has the following expression

where the sums run overall given $ i $-double degeneracy levels of total number $ n $, the fermion number operator $ n_{i} = a^{\dagger}_{i\uparrow}a^{}_{i\uparrow}+a^{\dagger}_{i\downarrow}a^{}_{i\downarrow} $ for the $ i $-th double degeneracy level, the single-particle energies $ \{\varepsilon _{i}\} $ obtained from the deform mean field. $ G>0 $ is the overall pairing interaction strength, and $ S^{+}_{i} = a^{\dagger}_{i\uparrow}a^{\dagger}_{i\downarrow} \; [S^{-}_{i} = (S^{+}_{i})^{\dagger} = a_{i\downarrow}a_{i\uparrow}] $ is pair creation [annihilation] operator. The up and down arrows in these expressions refer to time-reversed states.

Based on the Richardson-Gaudin method^[11-12], the exact $ k $-pair eigenstates of (1) can be given as

where $ \vert \nu_{i^{\prime}}\rangle $ is the pairing vacuum state with the seniority $ \nu_{i^{\prime}} $, here $ \nu_{i^{\prime}} = 0 $ for even systems or $ \nu_{i^{\prime}} = 1 $ for odd systems, in which $ i^{\prime} $ is the label of the level that is occupied by an unpaired single particle, namely, $ S^{-}_{i}\vert \nu_{i^{\prime}}\rangle = 0 $ and $ \hat{n}_{i}\vert \nu_{i^{\prime}}\rangle = \delta_{i i^{\prime}} \nu_{i}\vert \nu_{i^{\prime}}\rangle $ for all $ i $. The additional quantum number $ \xi $ is used to distinguish different eigenvectors with the same quantum number $ k $.

where the spectral parameters $ x_{\mu}^{(\xi)} $ ($ \mu = 1, 2, \cdots, k $) are the roots of the following Bethe ansatz equations (BAEs):

where the first sum runs over all $ i $-levels and $ \Omega_{i} = 1-\delta_{i i^{\prime}}\nu_{i^{\prime}} $. For each solution, the corresponding eigenenergy is given by

Due to the presence of singularities, the non-linear coupled Eq. (4) are notoriously difficult to solve, which limits the application of the Richardson-Gaudin method^{[14, 18-19]}. As shown in Refs. [20–23], the solutions of Eq. (4) can be found by solving the second-order Fuchsian equation^[18]

$ A(x) = \prod_{i = 1}^{n}({ x_{\mu}^{(\xi)} }-2\varepsilon_{i}) $ is an $ n $-degree polynomial,

$ V(x) $ are $ n-1 $ degree Van Vleck polynomials^[18], which are determined by Eq. (6). It is defined as

The definition of the polynomials $ P(x) $ is given as

in which $ k $ is the number of pairs, $ a_{i} $ are the expansion coefficients. When we set $ a_{k} = 1 $ in $ P(x) $, the coefficient $ a_{k-1} $ equals to the negative sum of the $ P(x) $ zeros, $ a_{k-1} = -\sum_{i = 1}^{k}{{ x_{i}^{(\xi)} }} = -E^{(\xi)}_{k} $.

Moreover, when the value of $ x $ approaches twice of the single-particle energy of a given level $ \delta $, i.e., $ x = 2\varepsilon_{\delta} $, Eq. (6) can be rewrite as^[21-22]

However, it is also challenging to get the root of the degree $ k $ polynomial in Eq. (10). In Refs. [20-21], by using Monte Carlo sampling, random initial guesses of the coefficients $ a_{0}, \cdots, a_{k-1} $ within the boundaries have been used to obtain the roots of the degree $ k $ polynomial. It is efficient when the system is small, and few initial guesses $ a_{0}, \cdots, a_{k-1} $ need to be solved simultaneously.

In Ref. [15], a new iterative algorithm is established for the exactly solvable pairing model by solving the polynomial approach in Eq. (10). This algorithm provides an efficient and robust method for calculating the eigenenergies and eigenstates of Eq. (1) for both spherical and deformed systems on a large scale. The new iterative approach begins by guessing the initial values of $ a_{0, \cdots, k-1} $ in Eq. (10) from a simple system with $ k = 1 $ and $ n = 1 $. The real form of $ P^0_{1}(x) = (a_{0}+x) $ is then found using the Newton-Raphson (NR) algorithm. The initial values $ {a_0^0, a_{1}^0} $ for the $k = 2,\, n = 2$ case are determined as $ P^{0}{2}(x) = P{1}(x)(x-2\varepsilon_{\delta}+r) $, where the random number $ r $ is generated using a Monte Carlo sampling box. By iterating this procedure $ k $ times, $ P_{k}(x) $ for the system with $ k $ pairs and $ n = k $ levels can be determined. The remaining $ n-k $ single-particle levels are then added in the next step, and the exact pairing solutions of the $ n $-level and $ k $-pair system are obtained. Using this new iterative approach, the $ k $-dimensional Monte Carlo sampling procedure in previous work^[20-21] has been reduced to a one-dimensional sampling procedure. This allows us to handle systems with 50 pairs and more than 100 levels under existing computing conditions, which is sufficient to address nuclear pairing problems. As a result, the exactly solvable pairing model can now be applied to extensive systems such as super-heavy nuclei.

Our previous study has revealed the crucial role of pairing correlation in fission barriers of Th, U, and Pu isotopes^[17]. The exactly solvable pairing model has been shown to be effective in investigating the properties of fissioning systems. In this paper, we use the efficient new iterative algorithm to systematically analyze the fission barriers of Th, Pa, U, Np, Pu, Am, Cm, Bk, and Cf isotope chains using the exactly solvable pairing model. The potential energy is calculated in the macroscopic-microscopic frame, using the Cassini ovaloids shape parametrization combined with the liquid drop model + Woods-Saxon potential^[24].

Geometrically, the Cassini ovaloids which is proposed by Pashkevich^[24–30] are obtained by rotating the curve around the $ z $ axis

where $ z $ and $ \rho $ being cylindrical coordinates, $ R_{0} $ is the radius of the spherical nucleus. The constant $ a $ is determined by volume conservation, which means that the family of shapes in Eq. (11) is only related to the elongation deformation parameter $ \epsilon $.

The deviation of the nuclear surface from Cassini ovaloids is defined by expansion of $ R(x) $ in series in Legendre polynomials $ P_{m}(x) $^{[24, 26]},

In the mac-mic framework, the total energy of a nucleus can be written as the sum of macroscopic and microscopic terms as follows,

where the macroscopic term $ E_{\rm{LD}}(N, Z) $ is approximated by the standard liquid drop model with neutron number $ N $ and proton number $ Z $. When calculating the potential energy surface, we only consider the energy $ E_{\rm{B}}(N, Z, \epsilon, \alpha_{m}) $ with the shape parameter $ \{\epsilon, \alpha_{m}\} $.

Here, the deformation correction energy is defined as $ E_{\rm{def}}(N, Z, \epsilon, \alpha_{m}) = [B_{s}-1]E_{s}^{0}+[B_{c}-1]E_{c}^{0} $, where $ B_{s} $ and $ B_{c} $ are functions of the $ \{\epsilon, \alpha_{m}\} $^[24]. The spherical surface energy is written as $ E_{s}^{0} = \alpha_{s}A^{\frac{2}{3}} $ with $ \alpha_{s} = 16 $ MeV. $ E_{c}^{0} = \alpha_{c}\frac{Z^{2}}{A} $ with $ \alpha_{c} = 0.71 $ MeV, in which $ A $ is the mass number, is the spherical Coulomb energy. The microscopic terms consist of two terms, the shell correction energy $ E_{\rm{shell}}^{\nu(\pi)}(N, Z, \epsilon, \alpha_{m}) $ proposed by Strutinsky^[31-32]. Here, we consider $ 200 $ single-particle levels for the shell correction energy calculations. The pairing correction energy $ E_{\rm{pair}}^{\nu(\pi)}(N, Z, \epsilon, \alpha_{m}) $ is obtained from Eq. (1) with doubly-degenerate levels, $ \nu (\pi) $ denotes the neutron (proton) pairs. For the pairing correction energy, we perform $ 29 $ single-particle levels around the neutron Fermi level and $ 16 $ single-particle levels around the proton Fermi level. The multi-dimensional potential energy surface is minimized in the elongation parameter $ \epsilon $ and the multipole deformation parameters ($ \alpha_{m}, m = 3, 4, 5, 6 $) simultaneously.

Generally, the pairing interaction strength is determined by the empirical formula or by fitting the odd-even mass differences^[33-34]. The recent study^[17] reveals that pairing correlation plays an essential role in the fission barrier height. Therefore, the odd-even mass differences (ground-state property) and the height of barriers (excited states property) should be used as experimentally observable quantities to determine the values for pairing interaction strength in the fission process. In this work, realistic values of pairing interaction strengths for isotope chains considered are obtained by fitting the experimental odd-even mass differences and the heights of the inner and outer barriers. The odd-even mass difference is defined as follows:

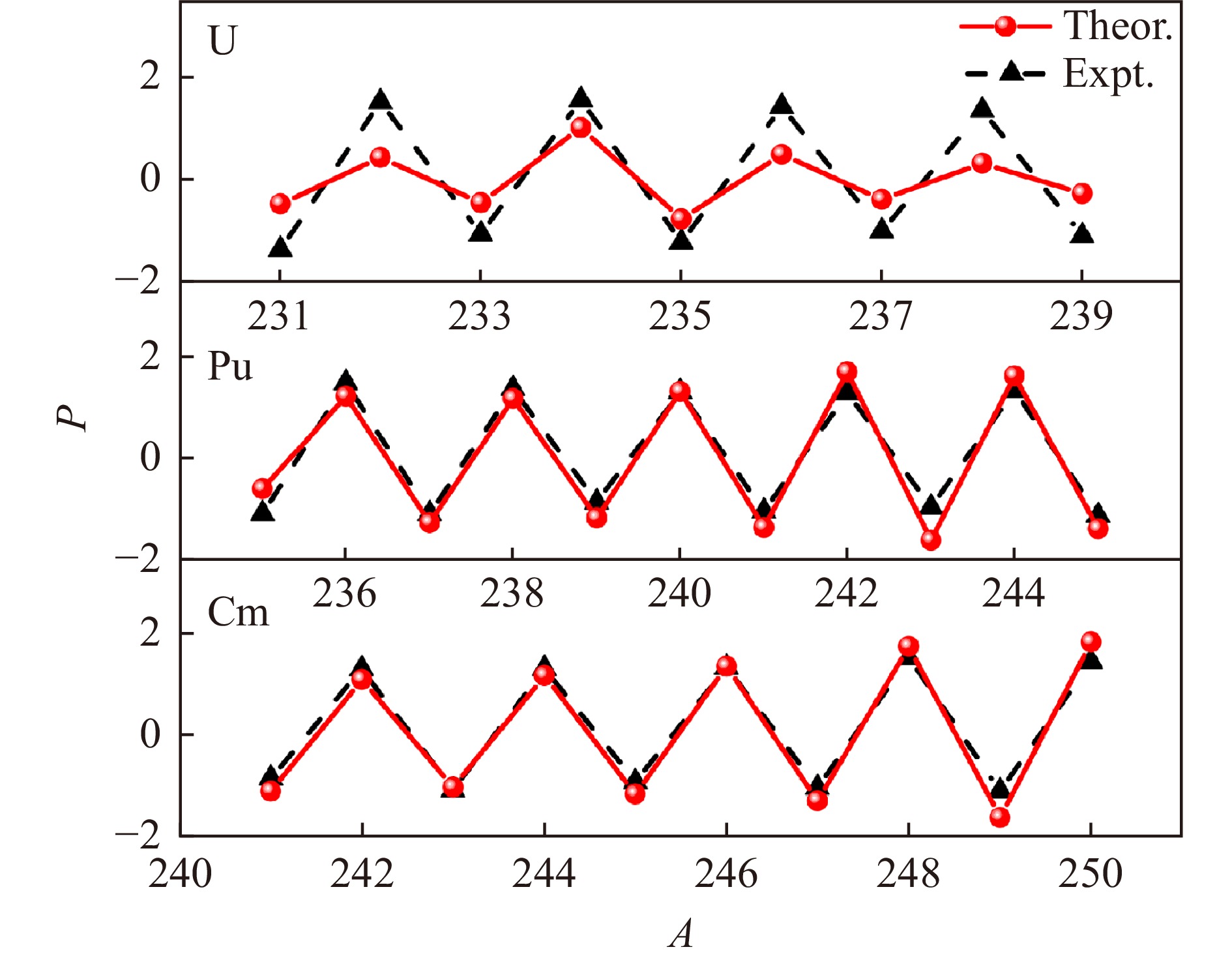
Figure 1 shows that our model calculations accurately reproduce the experimental odd-even mass differences for ^235-245Pu and ^241-250Cm isotopes with pairing strengths of $ G^{\nu} = 0.12 $ MeV and $ G^{\pi} = 0.18 $ MeV, respectively. However, for the ^231-239U isotopes, theoretical results show a deviation from the experimental data. To investigate this further, we analyzed the odd-even mass differences and the height of barriers for the ^231-239U isotopes using pairing interaction strengths of $ G^{\nu} = 0.12(G^{\pi} = 0.18) $ MeV and $ G^{\nu} = 0.15(G^{\pi} = 0.18) $ MeV, as shown in Fig. 2. We found that the odd-even mass differences for the ^224-238U isotopes were reproduced remarkably well by the model calculations with the pairing interaction strength $ G^{\nu} = 0.15 (G^{\pi} = 0.18) $ MeV, as shown in Fig. 2(a). On the other hand, as shown in Fig. 2(b) and (c), the results of the inner and outer fission barriers with $ G^{\nu} = 0.12(G^{\pi} = 0.18) $ MeV calculated in the current model are very close to the corresponding experimental values. In this work, taking into account the calculation results of the odd-even mass differences and the height of barriers in Fig. 2, we determined that the realistic values of pairing interaction strengths for the U isotope chains considered are $G^{\nu} = 0.12 (G^{\pi} = 0.18)$ MeV.

Figure 1.  The odd-even mass differences (in MeV) for ^231-239U^235-245Pu and ^241-250Cm. Experimental values are denoted as "Expt.", which are taken from Ref. [35], and theoretical values calculated in the exactly solvable pairing model are denoted as "Theor.". (color online)

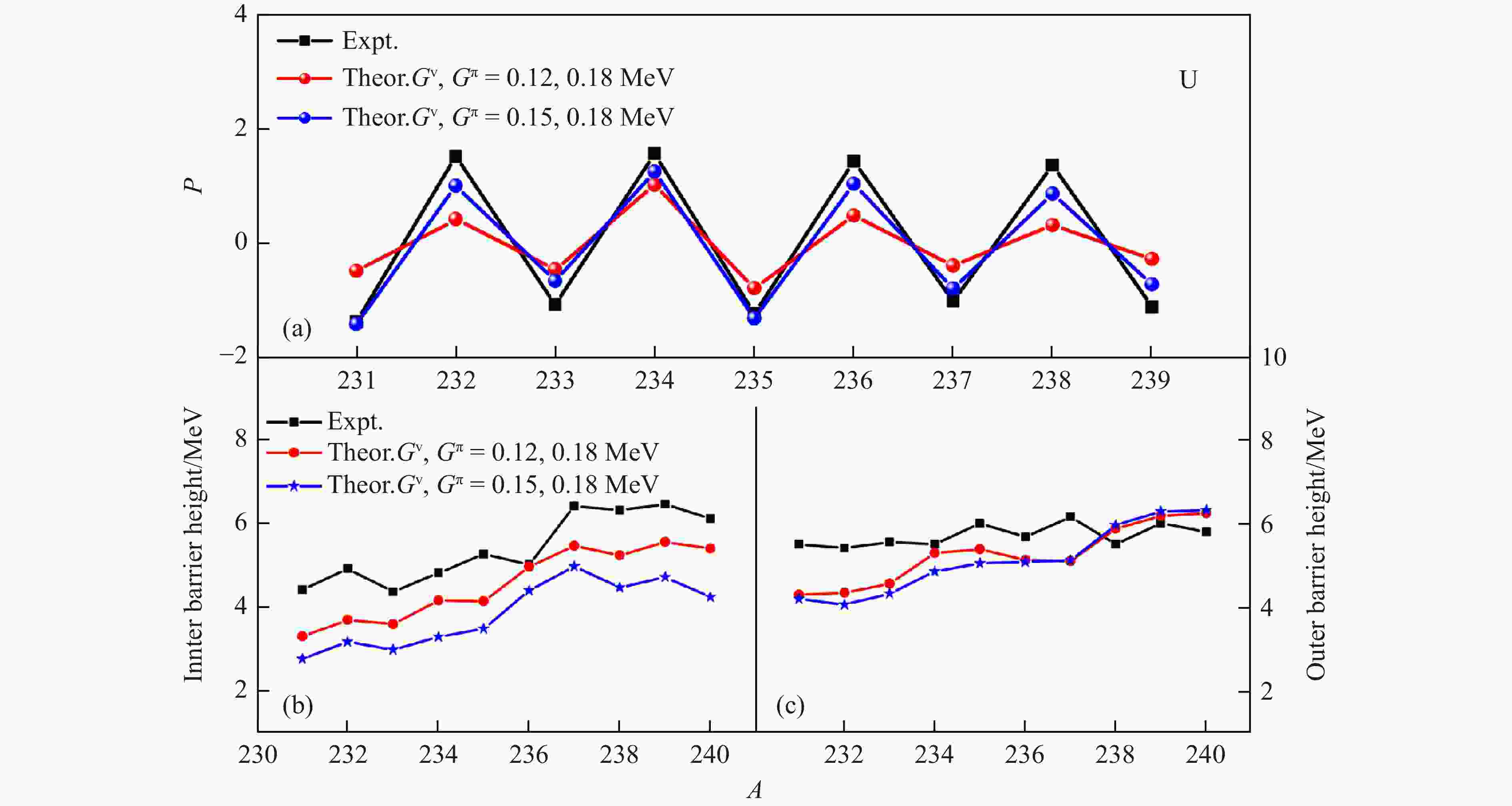
Figure 2.  The odd-even mass differences (in MeV), inner and outer fission barriers heights for U isotopes with given pairing interaction strengths. Experimental values are denoted as "Expt." and the theoretical values calculated in the present model are denoted as "Theor.". Experimental data are taken from Refs. [35, 36] (in MeV). A typical uncertainty in the experimental values, as suggested by the differences among various compilations, is of the order of ±0.5 MeV^[36]. (color online)

In this paper, we calculate the root-mean-square deviation $ \sigma $ (in MeV) of the odd-even mass differences to measure the overall variation in a data set. By analyzing the variation of $ \sigma $ caused by increasing pairing interaction strengths, we demonstrate that the odd-even mass difference can be used as an experimentally observable quantity to determine the realistic values of pairing interaction strength. The root-mean-square deviation $ \sigma $ is defined as

in which $ { E}_\mu^{\rm{Theor.}} $ are the theoretical values, $ {E}_\mu^{\rm{Expt.}} $ are the corresponding experimental estimates. $ {\cal{N}} $ is the number of the experimental data involved. Table 1 displays that the root-mean-square deviation decreasing from $\sigma_{\rm{U}} \sim 0.432$ MeV to $\sigma_{\rm{U}} \sim 0.329$ MeV by increasing the pairing strengths $ G^{\pi} $ from $ 0.10 $ to $ 0.12 $ MeV and $ G^{\nu} $ from $ 0.15 $ to $ 0.18 $ MeV. For Pu isotopes, when $ G^{\nu} = 0.15 $ MeV and $ G^{\pi} = 0.10 $ MeV, the theoretical value of the odd-even mass difference deviates from the experimental results with the root-mean-square deviation $ \sigma_{\rm{Pu}} = 0.223 $ MeV. By increasing the strengths to $ G^{\nu} = 0.12 $ MeV and $ G^{\pi} = 0.18 $ MeV, $ \sigma_{\rm{Pu}} $ decreases to $ 0.060 $ MeV. For Cm isotope chain, the value of $ \sigma_{\rm{Cm}} $ changes in a small region. $ G^{\nu} = 0.10 $ MeV and $ G^{\pi} = 0.18 $ MeV seem to yield a better result. The results in Table 1 observed that the odd-even mass difference can serve as one of the effective quantities to determine the neutron and proton pairing strengths.

In our study, published in Ref. [17], we conducted a systematic analysis of fission barriers and static fission paths in Th, U, and Pu isotopes using the deformed mean-field plus standard pairing model. Our results indicate that the pairing interaction plays different roles in different stages of the fission processes. Specifically, for ²²⁶Th, we found that the neutron pairing significantly affects the height of the inner barrier, while proton pairing has a greater effect on the outer barrier height. Building on this analysis, we extended our study to include a systematic investigation of fission barriers in nuclei spanning ^227-232Th, ^230-234Pa, ^231-240U, ^233-238Np, ^235-245Pu, ^239-245Am, ^244-249Bk, ^241-250Cm, and ^250-253Cf isotopes. By varying the pairing strength under our current model, we aimed to further elucidate the role of pairing interactions in the height of barrier. The results in Table 2 show that the height of the inner barrier is significantly affected by neutron pairing, while proton pairing affects the height of the outer barrier in Th, Pa, and U isotopes. For example, the root-mean-square deviation of the inner barrier changes by 30.9% in Th isotopes when the neutron pairing strengths $ G^{\nu} $ is varied by approximately 20%. In contrast, a variation of the proton pairing strengths $ G^{\pi} $ by the same amount results in a 10.3% change in the root-mean-square deviation of the inner barrier. For the outer barrier height, neutron pairing has a 5.9% effect on the root-mean-square deviation, while proton pairing has a 40.0% effect when varied by approximately 20%.

In contrast, for the Pu isotopes, we found that the height of the inner and outer barriers is affected equally by neutron and proton pairing. Specifically, a variation of approximately 20% in the pairing strengths $ G^{\nu} $ and $ G^{\pi} $ results in a 24.6% and 22.0% change in the height of the inner barrier, respectively, and a 6.52% and 10.9% change in the height of the outer barrier.

Interestingly, our analysis of the heavier isotopes of Cm and Cf shows that the role of neutron and proton pairing in fission barrier heights is reversed compared to the Th, Pa, U, and Pu isotopes. Specifically, our results indicate that neutron pairing has a greater influence on the height of the outer barrier, while proton pairing has a greater influence on the height of the inner barrier. For example, when the neutron pairing strength $ G^{\nu} $ is varied by approximately 20%, the root-mean-square deviation of the inner barrier height changes by 67.7% for Cm isotopes, while a variation of the proton pairing strength $ G^{\pi} $ by the same amount results in a 105.0% change in the height of the inner barrier for Cm isotopes.

These findings indicate that the role of neutron and proton pairing in fission barrier heights is not universal across all isotopes. Instead, the effect of pairing interactions can vary significantly depending on the specific isotopes being studied.

Following the previous analysis^[17], we advance a systematic study on fission barriers of nuclei ^227-232Th, ^230-234Pa, ^231-240U, ^233-238Np, ^235-245Pu, ^239-245Am, ^244-249Bk, ^241-250Cm and ^250-253Cf isotopes with the pairing strength parameters $ G^{\nu} = 0.12 $ MeV and $ G^{\pi} = 0.18 $ MeV under the current model. The root-mean-square deviation $ \sigma $ of the fission barrier height is used to measure the overall variation in theoretical values. As shown in Table 3, the deviations of the calculated inner barrier heights from the experimental estimates systematically less than 0.5 MeV $ \sigma_{\rm{inner}}<0.5 $ MeV, except for Th and Pa isotopes. While the calculated outer barrier heights yield an excellent agreement of the experimental data in those isotope chains, namely, $ \sigma_{\rm{outer}}<0.201 $ MeV.

Figures 3~5 shows that the theoretical barrier heights calculated by our model for the actinide isotope chains considered are close to the experimental estimates. The detailed results presented in Table 3 reveal that the deviations of the calculated inner barrier heights from the experimental estimates are systematically less than $ 0.5 $ MeV ($ \sigma_{\rm{inner}}<0.5 $ MeV), except for Th and Pa isotopes. Moverover, the calculated outer barrier heights show excellent agreement with the experimental data in those isotope chains, with $ \sigma_{\rm{outer}}<0.201 $ MeV.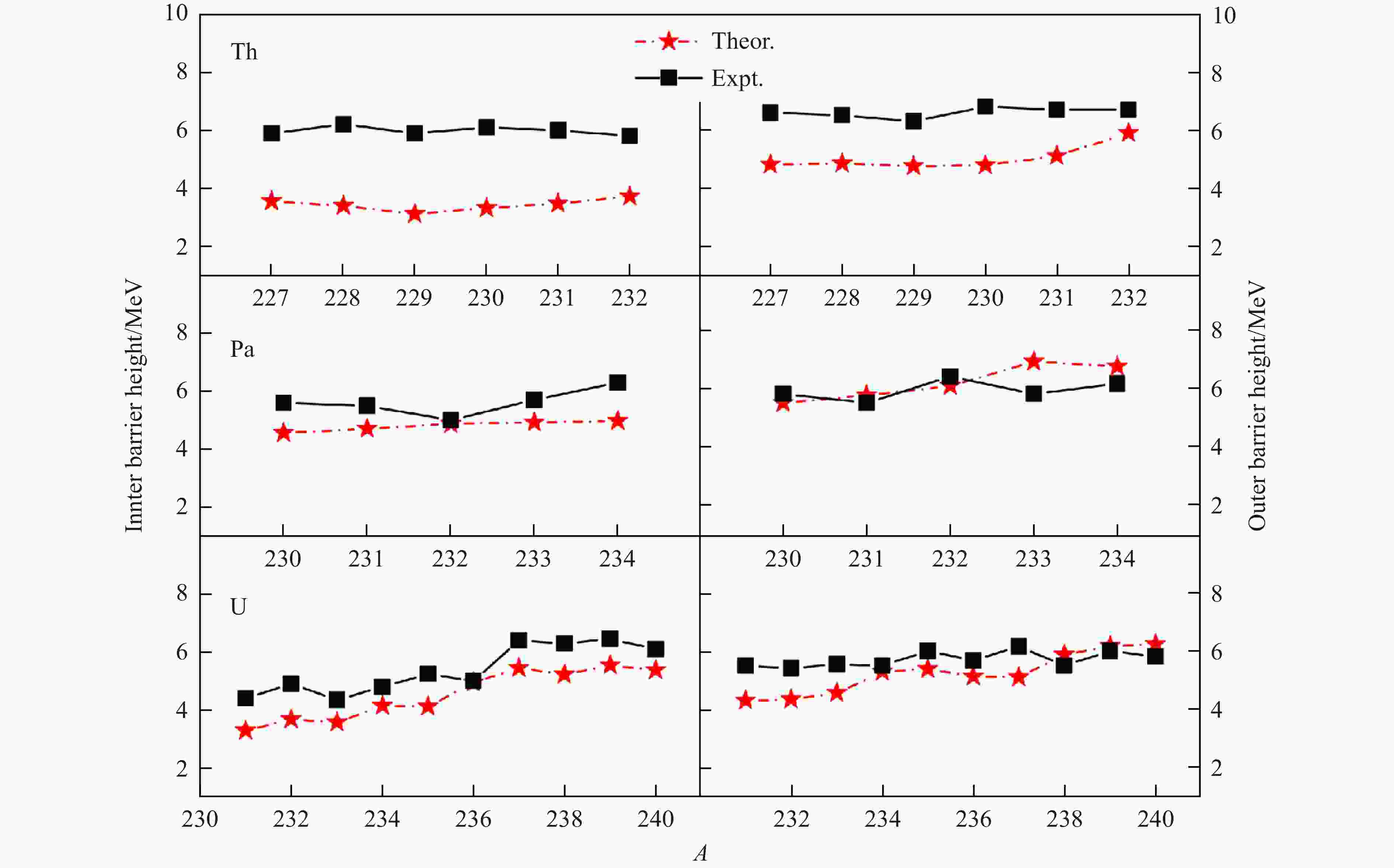

Figure 3.  Calculated inner and outer fission barrier heights for ^227-232Th, ^230-234Pa and ^231-240U. Theoretical values are compared to the experimental data in Ref. [36] (in MeV). (color online)

Figure 4.  Calculated inner and outer fission barrier heights for ^233-238Np, ^235-245Pu and ^239-245Am. Theoretical values are compared to the experimental data in Ref. [36] (in MeV). (color online)

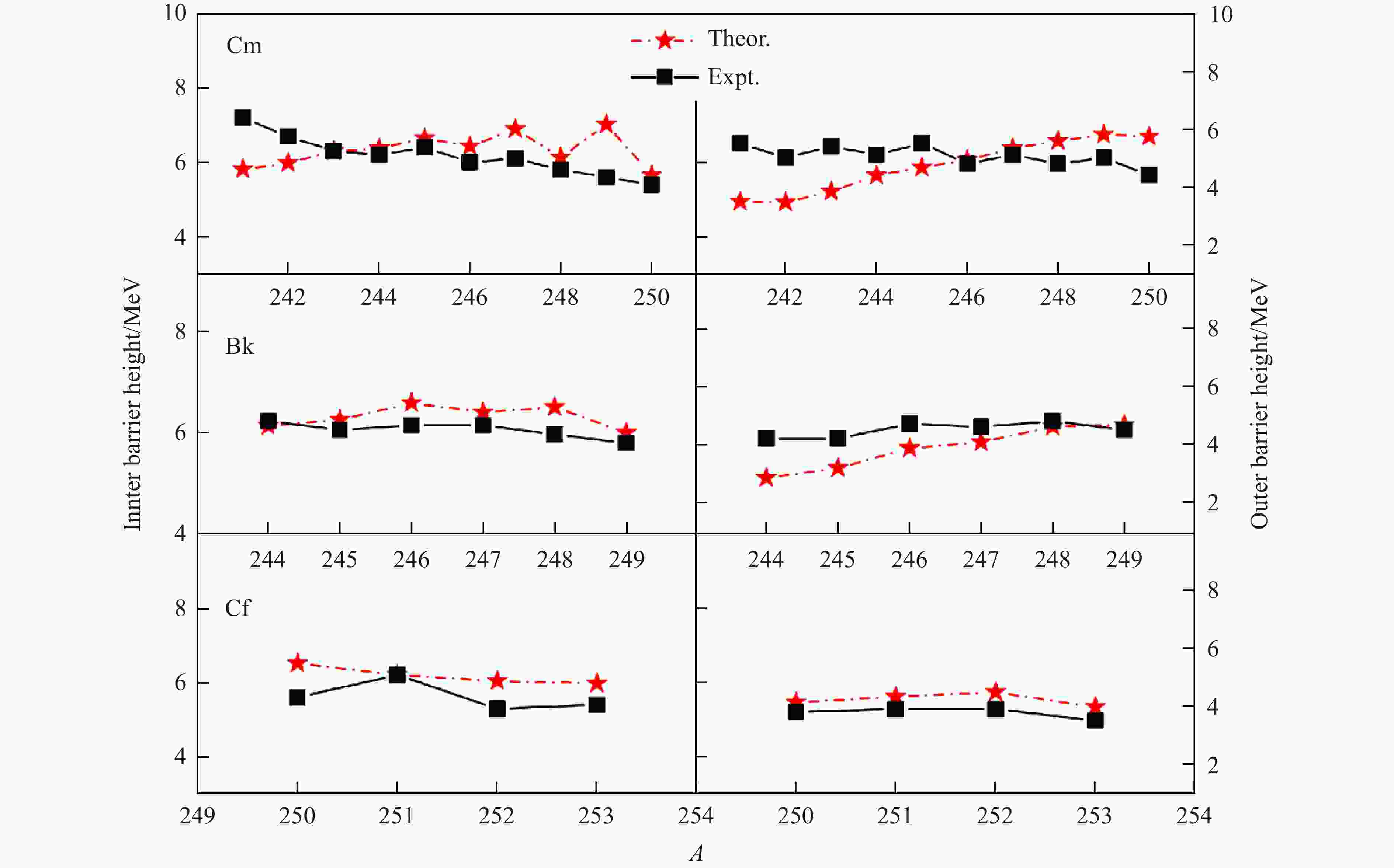
Figure 5.  Calculated inner and outer fission barrier heights for ^241-250Cm, ^244-249Bk and ^250-253Cf. Theoretical values are compared to the experimental data in Ref. [36] (in MeV). (color online)

In many other theoretical studies, the calculated inner barrier heights of light Th and Pa isotopes are also systematically lower than the experimental estimates^[36–40]. Based on the analysis above, we conclude that neutron pairing significantly impacts the inner barrier height for Th and Pa. The significant deviation in the inner barrier height of Th and Pa in Fig. 3 may be due to the strong neutron pairing interaction strength adopted. This observation may provide new insights and understanding of the mentioned anomaly for light actinides.

However, we acknowledge that there are conceptual difficulties in comparing calculated and experimental estimates due to the multi-dimensionality problem, i.e., the theoretical description of the fission process relates to a large number of deformation parameters. In addition, our study needs to provide more information on the effect of the proton and neutron correlation on the fission barrier height. Therefore, further verification of this hypothesis is necessary.

In particular, as shown in Fig. 4 for the Pu isotopes and Fig. 5 for the Cm isotopes, the theoretically calculated inner barrier heights exhibit odd-even staggering. Furthermore, as demonstrated in Fig. 6 (red points), the odd-even staggering vanishes when the pairing correction energy is neglected. This result confirms that the odd-even staggering of the inner barrier heights for Pu and Cm isotopes is indeed caused by the pairing interaction.

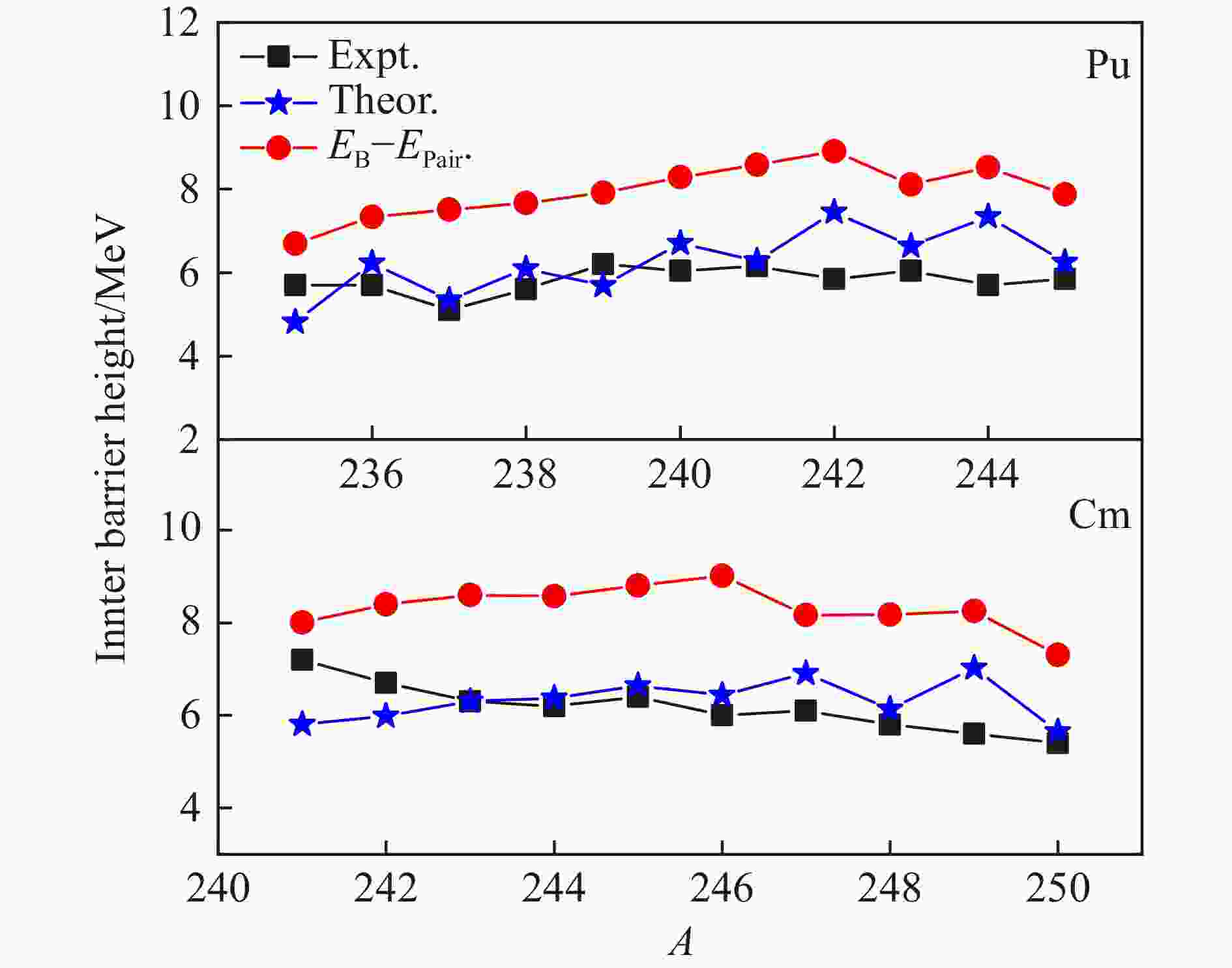
Figure 6.  Calculated inner fission barrier heights for ^235-245Pu and ^241-250Cm. Theoretical values and theoretical values without the pairing correction energy compared to the experimental data in Ref. [36] (in MeV). (color online)

Based on the results presented in this paper, we recommend using the odd-even mass differences (a ground-state property) and the height of barriers (an excited-state property) as experimentally observable quantities to determine the realistic values for pairing interaction strengths in the fission process. Numerical analysis of these observables can provide further insights into the impact of proton and neutron correlations on the fission barrier height.

The study investigates the impact of pairing correlations on the fission barriers of Th, Pa, U, Np, Pu, Am, Cm, Bk, and Cf isotope chains using the exactly solvable pairing model. The results show that pairing correlation is a significant factor in determining the fission barrier height, with varying impacts on different isotopes. For instance, in Th, Pa, and U isotopes, neutron pairing affects the height of the inner barrier, while proton pairing affects the outer barrier. On the other hand, in Pu isotopes, neutron and proton pairing affects both inner and outer barriers equally. Interestingly, the study finds that the role of neutron and proton pairing in fission barrier heights is reversed in heavier isotopes of Cm and Cf compared to lighter isotopes like Th and Pa. Specifically, neutron pairing influences the outer barrier height, while proton pairing affects the inner barrier height in Cm and Cf isotopes.

The study highlights the non-universal effect of pairing interactions on fission barriers across different isotopes, indicating that the exact nature of the interaction depends on the specific isotopes under study. The calculated barrier heights using the current model agree well with experimental data. The study suggests using odd-even mass differences and barrier heights as experimentally observable quantities to determine pairing interaction strengths in the fission process. However, the impact of self-consistent shell effects on fission barriers is not studied in this paper, which is an important consideration. Future work could explore an empirical formula for the pairing interaction strengths related to elongation deformation and fit experimentally observable quantities, such as odd-even mass differences, barrier heights, total kinetic energy distributions of fragments, and mass distributions, to further advance our understanding of fission barriers.