-
电荷半径是表征原子核大小的基本性质之一，原子核电荷半径的精确测量与预测对核结构的研究具有重要意义，例如它与原子核的同位旋[1-6]、壳层[7-10]以及形变效应[8]等有着密切的关联。对放射性核素电荷半径的观测研究发现了诸多奇特核物理现象，例如核的晕结构[11-18]、形状共存[19-23]、反转岛等奇特核物理现象[24]。此外，研究还发现了镜像核电荷半径之差与同位旋不对称度存在良好的线性关系[25]，这将有助于人们更精确地提取有关核物质在饱和密度附近的对称能信息[8, 26]。原子核电荷半径的研究不仅可以促进原子核相关理论的发展，而且也推动了实验上核激光谱学等多重技术的叠加发展。系统地研究原子核电荷半径对原子物理以及天体物理等相关学科也有重大意义。
实验上测量原子核电荷半径的方法一般分为两类[7]，其中一类是基于
$\mu$ 原子光谱或高能电子散射实验来测量电荷半径；另一类是基于激光光谱或$ K_{\alpha} $ X-射线测量一条同位素链上同位素位移进而得到原子核均方电荷半径之差。基于以上几种方法，目前实验上已经测量了超过1 000个核素的电荷半径[7, 25]。由于不稳定核素的产额以及电子散射靶等因素的限制，精密激光谱学成为了当前测量不稳定核素电荷半径的主要方法[27]。实验数据表明原子核的电荷半径与质量数$ A $ 有关，起初人们发现原子核的电荷半径可以用$ A^{1/3} $ 规律来描述，其最初的形式近似地表示为$ R=r_0A^{1/3} $ ，其中$r^{}_0$ 是电荷半径常数。国内科研人员研究发现$ Z^{1/3} $ 规律也可以很好地描述原子核的电荷半径[5-6, 28]。随着实验数据的不断增加，人们开始发现描述原子核电荷半径的公式还应该包含同位旋、壳效应以及形变等因素[1-10]。Wang等[29]结合Weizsäcker-Skyrme(WS*)核质量模型给出的壳修正能和形变参数，在文献[8]中基于$ A^{1/3} $ 规律考虑同位旋修正、壳修正以及形变修正提出了一个描述原子核电荷半径的四参数公式，其计算结果与实验测量结果的均方根偏差仅为0.022 fm。Sheng等[30]通过对比基于$ A^{1/3} $ 和$ Z^{1/3} $ 规律描述核电荷半径的精度发现，随着修正因素的增多，用$ A^{1/3} $ 规律描述核电荷半径呈现出了一定的优势。除了上述的一些经验公式可以较好地描述原子核电荷半径之外，基于密度泛函理论的微观原子核理论方法也可以描述核的电荷半径，例如Skyrme Hartree-Fock-Bogoliubov(HFB)[31-33]和Relativistic Mean Field(RMF)[34]模型等，其中HFB25模型[31]的计算结果与实验数据的均方根偏差为0.025 fm，这与文献[8]中的计算结果是可比拟的。除此之外，一些局域关系[35-37]也可以很好地预测原子核电荷半径，例如Garvey-Kelson(GK)关系，虽然这些局域关系可以更好地再现实验数据，但是随着外推距离的增加其不确定度会迅速增大。因此，寻找有效的方法来进一步提高理论方法预测原子核电荷半径的精度是极其重要的。最近，机器学习方法被广泛地应用于核物理的研究[38]。例如早在2011年Wang等[39]就已经将径向基函数方法用于提高原子核质量模型的预测精度，后来人们进一步发展了考虑奇偶效应的径向基函数方法来提高原子核质量模型的精度[40-43]，Ma等[44]基于径向基函数方法进一步提高了预测原子核
$ \alpha $ 衰变半衰期的精度。最近贝叶斯神经网络方法在核物理的研究中得到了更为广泛地应用，例如在原子核质量预测[45]、裂变产额评价[46-47]、$ \alpha $ 衰变半衰期预测[48]、原子核对称能[49]以及核反应[50]等研究中均都验证了贝叶斯神经网络方法的有效性。Wu等[51-52]发现核岭回归方法也可以有效提高原子核质量模型的预测精度。基于以上研究不难发现，机器学习在提高原子核理论模型的预言精度上可以起到至关重要的作用。因此，基于机器学习能否进一步提高理论模型预测原子核电荷半径的精度具有重要的研究意义。本文将基于径向基函数方法尝试进一步提高理论模型预言原子核电荷半径的精度，其中理论方法主要考虑HFB25模型以及基于WS*核质量模型给出的壳修正能和形变参数提出的原子核电荷半径公式。文中第二部分将介绍径向基函数方法的理论框架，第三部分是结果与讨论，最后给出总结。
-
径向基函数(Radial Basis Functions, RBF)方法被广泛地用于曲面重建与修复，在改善原子核质量模型预言能力方面也取得了非常好的效果。RBF的表达式通常写为
$$ S(X)=\sum\limits_{i=1}^{m} \omega_{i} \phi\left(\left\|X-X_{i}\right\|\right) \; {\rm{，}} $$ (1) 其中：
$ X_{i} $ 为测量数据点；$ \omega_{i} $ 是点$ X_{i} $ 的权重因子；$ \phi $ 是基函数；$ \left\|X-X_{i}\right\| $ 是欧几里得范数；$ m $ 是所有数据点的总数。给定$ m $ 个样本$(X_i,\, f_i)$ ，得到光滑函数$ S(X) $ ，使其满足$ S(X_i)=f_i $ 。RBF的权重因子可以通过矩阵求解得到，其形式如下：$$ \begin{array}{l} \left(\begin{array}{c}\omega_{1} \\ \omega_{2} \\ \cdots \\ \omega_{m}\end{array}\right)=\left(\begin{array}{cccc}\phi_{11} & \phi_{12} & \cdots & \phi_{1 m} \\ \phi_{21} & \phi_{22} & \cdots & \phi_{2 m} \\ \cdots & \cdots & \cdots & \cdots \\ \phi_{m 1} & \phi_{m 2} & \cdots & \phi_{m m}\end{array}\right)^{-1}\left(\begin{array}{c}f_{1} \\ f_{2} \\ \cdots \\ f_{m}\end{array}\right) \; {\rm{，}} \end{array} $$ (2) 其中
$ \phi_{i j}=\phi\left(\left\|X_{i}-X_{j}\right\|\right)(i, j=1, \ldots, m) $ ；本工作中采用线性基函数$ \phi(x)=x=\sqrt{\left(Z_{i}-Z_{j}\right)^{2}+\left(N_{i}-N_{j}\right)^{2}} $ ，Z表示质子数，N表示中子数。为了获得式(2)中的权重，实验测量值与理论计算结果的偏差$ \Delta r(Z, N)=r^{\exp }(Z, N)-r^{{\rm{th }}}(Z, N) $ 将作为被重建的对象。RBF改善后的模型预测值为$$ \begin{array}{l} r^{{\rm{RBF}}}(Z, N)=r^{{\rm{th }}}(Z, N)+S(Z, N) \; {\rm{，}} \end{array} $$ (3) 对于未知原子核电荷半径的预测可以看成是针对原子核电荷半径曲面的外推与内插问题。在本工作中，基于文献[7]给出的885个(
$Z \geqslant 8,~N \geqslant 8$ ) 原子核电荷半径实验数据，对WS*和HFB25两个模型的预言能力进行研究。为了区分，基于RBF修正的两个模型的预测结果分别表示为WS*+RBF和HFB25+RBF。采用均方根偏差来评价模型结合RBF方法预测原子核电荷半径的能力，其形式如下：$$ \sigma=\sqrt{\frac{1}{m} \sum\limits_{i=1}^{m}\Big[r_{i}^{\exp }(Z, N)-r_{i}^{{\rm{th}}}(Z, N)\Big]^{2}} \; {\rm{。}} $$ (4) 如果均方根偏差
$ \sigma $ 越小，就说明模型描述现有的实验数据越精确。 -
首先，本研究工作基于885个原子核电荷半径实验数据进行留一交叉验证，即某一个待预测原子核电荷半径是由除其本身之外其余所有实验数据基于RBF方法确定的光滑函数
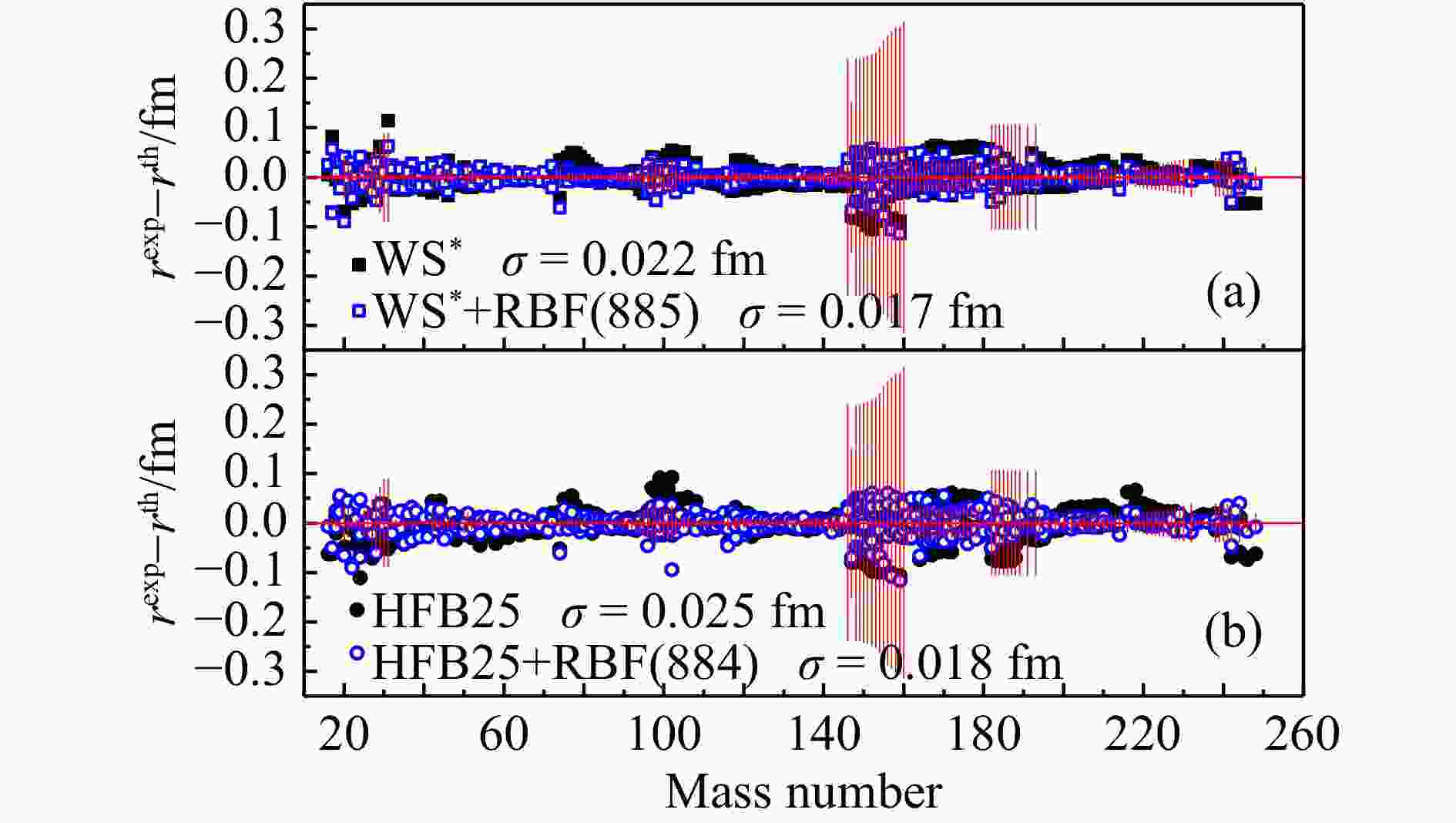
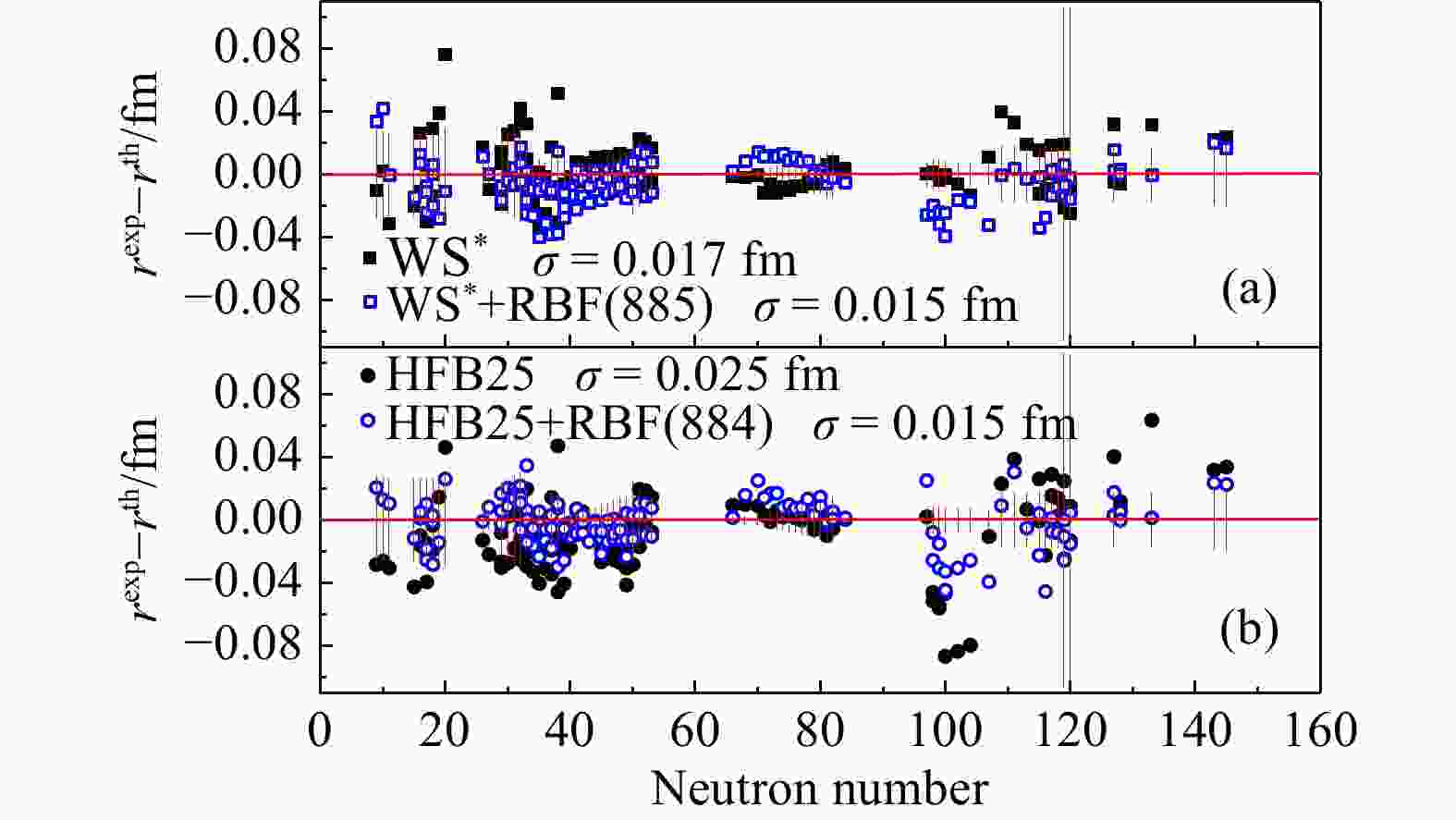
$S(N,\, Z)$ 来预言。换言之，从885个已测量的核电荷半径数据中选取884个数据获取$S(N,\, Z)$ ，用得到的$S(N,\, Z)$ 再计算目标核的电荷半径。图1 给出了RBF方法通过留一交叉验证来改善HFB25和WS*两个模型的计算结果与实验值的偏差，可以看到RBF方法大幅度地降低了两个模型结果与实验值的偏差，其中WS*模型计算结果的均方根偏差降低了22.7%，HFB25模型计算结果的均方根偏差降低了28.0%。其次，基于885个实验数据进行RBF拟合得到$S(N,\, Z)$ ，然后用得到的$S(N,\, Z)$ 值再预言144个新测量的原子核电荷半径，其中129个新的实验数据来自文献[25]，另外15个新的实验数据基于文献[25]中的式(1)和(2)结合参考文献[53-58]提供的均方电荷半径之差计算得到，其得到的均方根电荷半径和不确定度在表 1中列出。图2呈现了HFB25和WS*两个模型及其RBF方法改善后的预言结果与144个最新实验值的偏差。可以看出，不加RBF方法修正WS*模型的预言结果要稍好一些，而加了RBF方法修正后两个模型的预言结果普遍得到了改善，其中WS*模型预言结果的均方根偏差降低了11.8%，HFB25模型预言结果的均方根偏差降低了40.0%。从图2(a)可以看到，在中子数$N = 100$ 附近WS*+RBF的预言结果反而变差了，这可能是因为在其附近的$ ^{181, 183, 185}{\rm{Hg}} $ 等核素的形状共存现象导致的。由于WS*模型没有较好地再现这些形状共存核的电荷半径变化趋势，因此利用RBF方法训练这些奇特原子核获得的信息可能会对预言附近核素的电荷半径造成负面影响。
图 1 885个原子核电荷半径实验值与理论预测值的偏差(在线彩图)
表 1 15个新的原子核电荷半径实验数据及其误差*
$ Z $ $ A $ $ \delta<r^{2}>$$/{\rm{fm}}^2$ $ \Delta \delta<r^{2}> $$/{\rm{fm}}^2$ $ r^{\exp }$/fm $ \Delta r^{\exp }$/fm 19 52 0.790[53] 0.14 3.548 0 0.019 7 46 112 0.352[54] 0.012 4.594 8 0.003 0 46 114 0.475[54] 0.011 4.608 1 0.002 9 46 116 0.560[54] 0.020 4.617 3 0.003 5 46 118 0.632[54] 0.035 4.625 1 0.004 6 49 128 0.630[55] 0.090 4.683 3 0.009 7 49 129 0.691[55] 0.088 4.689 9 0.009 7 49 130 0.741[55] 0.098 4.695 2 0.010 7 49 131 0.747[55] 0.098 4.695 8 0.010 7 76 194 0.034[56] 0.035 5.415 7 0.003 6 76 196 0.177[56] 0.055 5.428 9 0.005 3 77 196 0.160[57] 0.030 5.411 6 0.105 8 77 197 0.230[57] 0.020 5.418 1 0.105 7 80 207 0.503[58] 0.035 5.492 3 0.004 4 80 208 0.624[58] 0.044 5.503 3 0.005 0 *第一列代表质子数，第二列代表质量数，第三列代表均方电荷半径之差，第四列代表均方电荷半径之差的误差，第五列代表原子核均方根电荷半径，第六列代表原子核均方根电荷半径的误差。 
图 2 144个最新的原子核电荷半径实验值与理论预测值的偏差(在线彩图)
虽然通过激光核谱学实验可以获取较多核素的同位素位移数据，进而可以得到相对的均方电荷半径之差，但是由于部分同位素链上缺少绝对的均方根电荷半径实验数据，因此得不到该同位素链上均方根电荷半径的实验值，例如At和Ac同位素链。所以要想基于At或Ac等同位素链的实验数据检验理论计算结果，就需要将理论计算的均方根电荷半径转换成均方电荷半径之差。图3呈现了
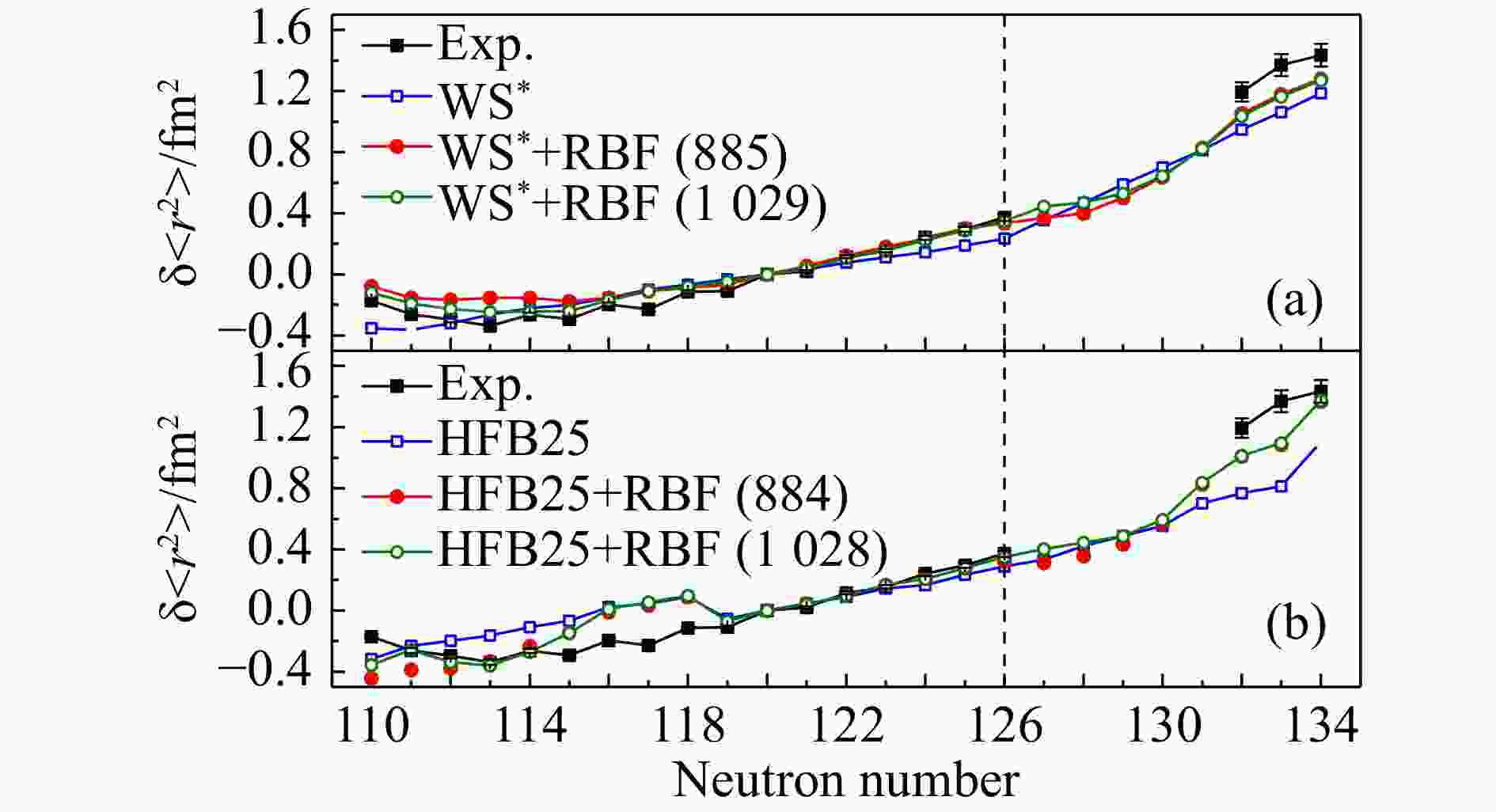
$ ^{195-219}{\rm{At}} $ 的均方电荷半径之差，其中实心方块代表基于同位素位移和原子核质量的实验值结合理论计算的质量位移和场位移系数确定的实验值。图3(a)中的空心方块代表WS*模型的计算值，实心圆代表基于RBF方法训练885个实验数据后WS*+RBF的结果，空心圆代表基于RBF方法训练1 029个实验数数据后WS*+RBF的结果；类似的，图3(b)中给出了HFB25模型及其结合RBF方法修正的结果。从图3中可以看到，WS*模型计算的结果可以较好地再现中子幻数$N = 126$ 引起的突变行为，然而这种突变行为在RBF方法修正后却消失，这可能是因为在$ {\rm{At}} $ 同位素链附近的其它同位素链上$N = 126$ 之后的实验数据缺失造成的；HFB25模型及其RBF方法修正后的结果都没能再现中子幻数$N = 126$ 引起的突变行为。从图3中还可以看到，在中子数$ = 110 \sim 118$ 附近WS*模型经过RBF方法训练1 029个实验数据修正后的结果要比训练885个实验数据的结果偏好，HFB25模型也呈现了类似的结果，这可能是因为实验数据中新增加了$ {\rm{Po}}^{109, 111, 113, 115, 117, 119} $ 的均方根电荷半径带来的有利影响。
图 3 At同位素链均方电荷半径之差的理论预测与实验值(在线彩图)
由于实验上很难测到超重区原子核的电荷半径，目前原子核电荷半径实验数据只包含到质子数
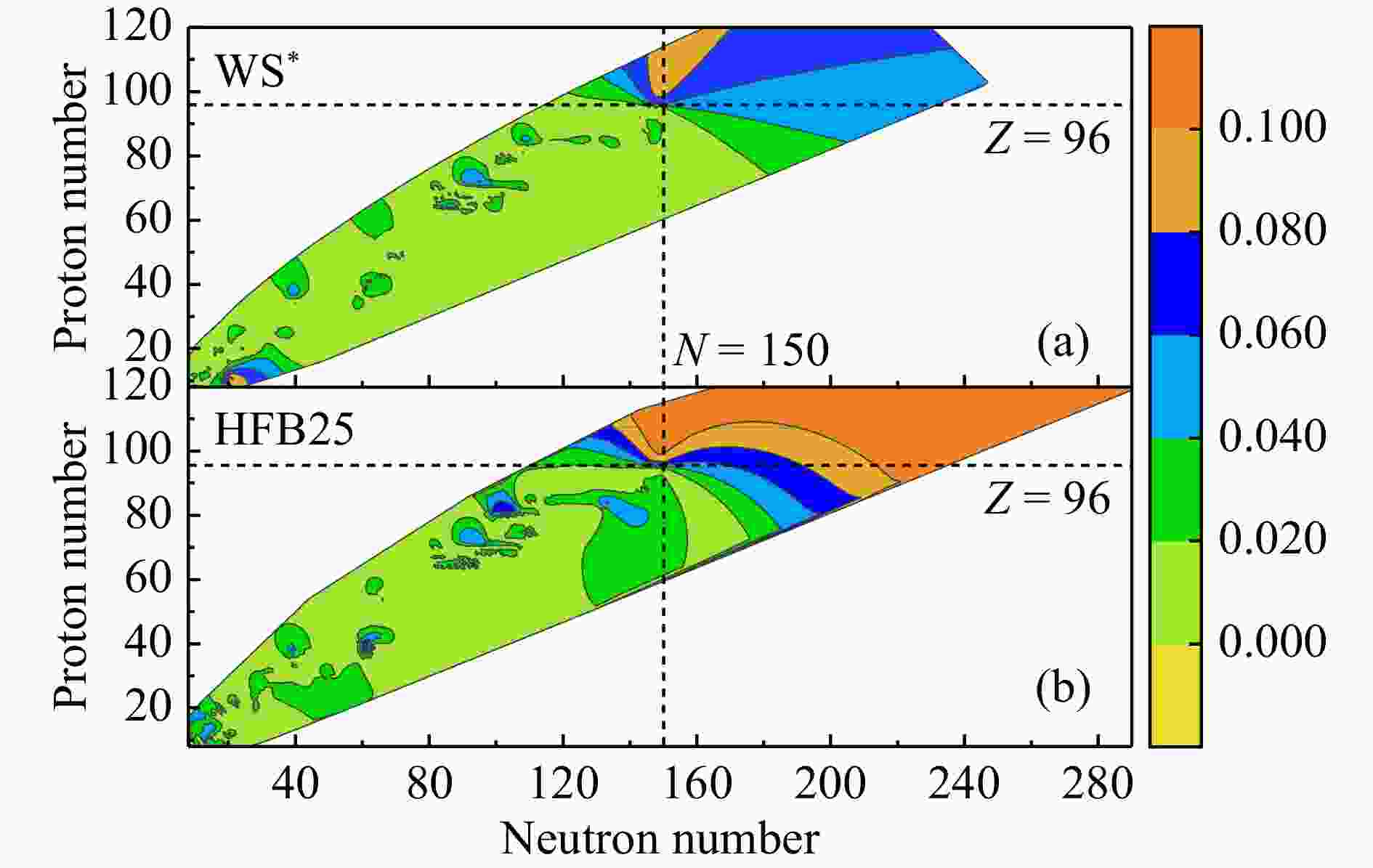
$Z = 96$ 的同位素链，因此基于理论模型预言超重区域原子核电荷半径显得尤为重要。图4给出了HFB25和WS*两个模型基于RBF方法训练1 029个原子核电荷半径实验数据($N \geqslant 8, \, Z \geqslant 8$ )后修正值的绝对值等高线图。从图4可以看出，RBF方法对于WS*模型在超重区域的修正值大部分可以保持在0.1 fm以内，而对于HFB25模型在超重区域的修正值大部分都超过了0.1 fm，这表明HFB25模型在描述超重核电荷半径方面有待进一步提高。这些信息对于分析模型误差以及进一步改善原子核电荷半径的预言精度非常有用。
图 4 HFB25和WS*两个模型基于RBF方法训练1 029个原子核电荷半径实验数据(
$N \geqslant 8,\,Z \geqslant 8$ )后修正值的绝对值等高线图(在线彩图) -
结合RBF方法，有效地提高了HFB25和WS*两个模型预言原子核电荷半径的精度。首先，基于885个原子核电荷半径实验数据进行留一交叉验证，使WS*模型计算结果的均方根偏差降低了22.7%，HFB25模型计算结果的均方根偏差降低了28.0%；其次，基于885个实验数据进行RBF拟合得到
$ S(N, \, Z) $ ，然后用得到$ S(N, \, Z) $ 的值再预言144个新测量的原子核电荷半径，其中WS*模型预言结果的均方根偏差降低了11.8%，HFB25模型预言结果的均方根偏差降低了40.0%。此外，基于$ {\rm{At}} $ 同位素链的均方电荷半径之差实验数据检验发现，在实验数据匮乏区域，使用RBF修正方法可能会降低模型的预言精度；而随着实验数据的增加，RBF修正方法会提高模型的预言精度。最后，本工作还研究了RBF方法对HFB25和WS*两个模型在超重区域预言值的修正程度，结果发现RBF方法对于WS*模型在超重区域的修正值大部分可以保持在0.1 fm以内，而对于HFB25模型在超重区域的修正值大部分都超过了0.1 fm，这表明HFB25模型在描述超重核电荷半径方面有待进一步提高。
-
摘要: 结合径向基函数方法有效地提高了两个全局模型预言原子核电荷半径的精度和能力。利用885个原子核电荷半径实验数据进行留一交叉验证，Skyrme Hartree-Fock-Bogoliubov(HFB25)模型的计算结果与实验测量结果的均方根偏差从0.025 fm降到了0.018 fm，基于Weizsäcker-Skyrme (WS*)核质量模型给出的壳修正能和形变参数提出的四参数公式的计算结果与实验测量结果的均方根偏差从0.022 fm降到了0.017 fm。两个模型结合径向基函数方法预言最新的144个实验值的均方根偏差仅为0.015 fm。通过研究径向基函数方法对HFB25和WS*两个模型在超重区域预言值的修正程度发现，径向基函数方法对于WS*模型在超重区域的修正值大部分可以保持在0.1 fm以内，而对于HFB25模型在超重区域的修正值大部分都超过了0.1 fm，这对于分析模型误差以及进一步改善原子核电荷半径的预言精度非常有用。Abstract: Accuracy and predictive power of two global models to predict nuclear charge radius are significantly improved combined with the radial basis function(RBF) approach. The root-mean-square(rms) deviation of Skyrme Hartree-fock-Bogoliubov(HFB25) model is reduced from 0.025 to 0.018 fm, using 885 experimental data of the nuclear charge radius to leave-one-out cross validation, the rms deviation of a formula proposed based on the shell correction energies and deformation parameters given by the Weizäcker-Skyrme(WS*) nuclear mass model is reduced from 0.022 to 0.017 fm. For the latest 144 experimental data, the rms deviations of HFB25 and WS* models combined with RBF approach are only 0.015 fm. With the RBF approach, by studying the correction degree of prediction values of HFB25 and WS* models in the superheavy region, it is found that the correction degree of WS* model in the superheavy region can be kept within 0.1 fm, while the correction degree of HFB25 model in the superheavy region is more than 0.1 fm. This is very useful for analyzing model errors and further improving the prediction accuracy of nuclear charge radius.
-
Key words:
- charge radius /
- radial basis function /
- root-mean-square deviation /
- superheavy nucleus
-
图 1 885个原子核电荷半径实验值与理论预测值的偏差(在线彩图)
(a) 为WS*模型及其RBF方法修正的结果，(b) 为HFB25模型及其RBF方法修正的结果，红色竖线表示实验值的测量误差。(备注：由于HFB25模型没有给出$ ^{17}{\rm{Ne}} $的计算结果，但是实验上测到了$ ^{17}{\rm{Ne}} $的电荷半径，因此HFB25模型结合径向基函数方法的训练集比WS*模型少了一个数据点。
图 2 144个最新的原子核电荷半径实验值与理论预测值的偏差(在线彩图)
(a) 为WS*模型及其RBF方法修正后的结果，(b) 为HFB25模型及其RBF方法修正后的结果，红色竖线表示实验值的测量误差。
图 4 HFB25和WS*两个模型基于RBF方法训练1 029个原子核电荷半径实验数据(
$N \geqslant 8,\,Z \geqslant 8$ )后修正值的绝对值等高线图(在线彩图)表 1 15个新的原子核电荷半径实验数据及其误差*
$ Z $ $ A $ $ \delta<r^{2}>$$/{\rm{fm}}^2$ $ \Delta \delta<r^{2}> $$/{\rm{fm}}^2$ $ r^{\exp }$/fm $ \Delta r^{\exp }$/fm 19 52 0.790[53] 0.14 3.548 0 0.019 7 46 112 0.352[54] 0.012 4.594 8 0.003 0 46 114 0.475[54] 0.011 4.608 1 0.002 9 46 116 0.560[54] 0.020 4.617 3 0.003 5 46 118 0.632[54] 0.035 4.625 1 0.004 6 49 128 0.630[55] 0.090 4.683 3 0.009 7 49 129 0.691[55] 0.088 4.689 9 0.009 7 49 130 0.741[55] 0.098 4.695 2 0.010 7 49 131 0.747[55] 0.098 4.695 8 0.010 7 76 194 0.034[56] 0.035 5.415 7 0.003 6 76 196 0.177[56] 0.055 5.428 9 0.005 3 77 196 0.160[57] 0.030 5.411 6 0.105 8 77 197 0.230[57] 0.020 5.418 1 0.105 7 80 207 0.503[58] 0.035 5.492 3 0.004 4 80 208 0.624[58] 0.044 5.503 3 0.005 0 *第一列代表质子数，第二列代表质量数，第三列代表均方电荷半径之差，第四列代表均方电荷半径之差的误差，第五列代表原子核均方根电荷半径，第六列代表原子核均方根电荷半径的误差。 
下载: 导出CSV
-
[1] NERLO-POMORSKA B, POMORSKI K. Z Phys A, 1993, 344: 359. doi: 10.1007/BF01283190 [2] NERLO-POMORSKA B, POMORSKI K. Z Phys A, 1994, 348: 169. doi: 10.1007/BF01291913 [3] ANGELI I, APH N S. Heavy Ion Physics, 2001, 13: 149. doi: 10.1556/APH.13.2001.1-3.17 [4] LI R H, HU Y M, LI M C. Chin Phys C, 2009, 33(Suppl. I): 123. [5] ZHANG S Q, MENG J. Eur Phys J A, 2002, 13: 285. doi: 10.1007/s10050-002-8757-6 [6] LEI Y A, ZHANG Z H, ZENG J Y. Commun Theor Phys, 2009, 51: 123. doi: 10.1088/0253-6102/51/1/23 [7] ANGELI I, MARINOVA K P. At Data Nucl Data Tables, 2013, 99: 69. doi: 10.1016/j.adt.2011.12.006 [8] WANG N, LI T. Phys Rev C, 2013, 88: 011301(R). doi: 10.1103/PhysRevC.88.011301 [9] ANGELI I, MARINOVA P. J Phys G: Nucl Part Phys, 2015, 42: 055108. doi: 10.1088/0954-3899/42/5/055108 [10] SHENG Z Q, FAN G W, QIAN J F, et al. Eur Phys J A, 2015, 51: 40. doi: 10.1140/epja/i2015-15040-1 [11] WANG L B, MUELLER P, BAILEY K, et al. Phys Rev Lett, 2004, 93: 142501. doi: 10.1103/PhysRevLett.93.142501 [12] MUELLER P, SULAI I A, VILLARI A C C, et al. Phys Rev Lett, 2007, 99: 252501. doi: 10.1103/PhysRevLett.99.252501 [13] LU Z T, MUELLER P, DRAKE G W F, et al. Rev Mod Phys, 2013, 85: 1383. doi: 10.1103/RevModPhys.85.1383 [14] SÁNCHEZ R, NÖRTERSHÄUSER W, EWALD G, et al. Phys Rev Lett, 2006, 96: 033002. doi: 10.1103/PhysRevLett.96.033002 [15] NÖRTERSHÄUSER W, SÁNCHEZ R, EWALD G, et al. Phys Rev A, 2011, 83: 012516. doi: 10.1103/PhysRevA.83.012516 [16] NÖRTERSHÄUSER W, TIEDEMANN D, ŽÁKOVÁ M, et al. Phys Rev Lett, 2009, 102: 062503. doi: 10.1103/PhysRevLett.102.062503 [17] GEITHNER W, NEFF T, AUDI G, et al. Phys Rev Lett, 2008, 101: 252502. doi: 10.1103/PhysRevLett.101.252502 [18] MARINOVA K, GEITHNER W, KOWALSKA M, et al. Phys Rev C, 2011, 84: 034313. doi: 10.1103/PhysRevC.84.034313 [19] ULM G, BHATTACHERJEE S K, DABKIEWICZ P, et al. Z Phys A, 1986, 325: 247. doi: 10.1007/BF01294605 [20] MARSH B A, DAY GOODACRE T, SELS S, et al. Nat Phys, 2018, 14: 1163. doi: 10.1038/s41567-018-0292-8 [21] SELS S, DAY GOODACRE T, MARSH B A, et al. Phys Rev C, 2019, 99: 044306. doi: 10.1103/PhysRevC.99.044306 [22] COCOLIOS T E. Hyperfine Interact, 2017, 238: 16. doi: 10.1007/s10751-016-1391-5 [23] YANG X F, WRAITH C, XIE L, et al. Phys Rev Lett, 2016, 116: 182502. doi: 10.1103/PhysRevLett.116.182502 [24] 白世伟, 杨晓菲. 原子核物理评论, 2018, 35(4): 382. doi: 10.11804/NuclPhysRev.35.04.382 BAI S W, YANG X F. Nuclear Physics Review, 2018, 35(4): 382. (in Chinese) doi: 10.11804/NuclPhysRev.35.04.382 [25] LI T, LUO Y N, WANG N. At Data Nucl Data Tables, 2021, 140: 101440. doi: 10.1016/j.adt.2021.101440 [26] ALEX BROWN B. Phys Rev Lett, 2017, 119: 122502. doi: 10.1103/PhysRevLett.119.122502 [27] 刘永超, 白世伟, 杨晓菲. 原子核物理评论, 2019, 36(2): 161. doi: 10.11804/NuclPhysRev.36.02.161 LIU Y C, BAI S W, YANG X F. Nuclear Physics Review, 2019, 36(2): 161. (in Chinese) doi: 10.11804/NuclPhysRev.36.02.161 [28] 曾谨言. 物理学报, 1975, 24(2): 151. doi: 10.7498/aps.24.151 ZENG J Y. Acta Phys Sin, 1975, 24(2): 151. (in Chinese) doi: 10.7498/aps.24.151 [29] WANG N, LIANG Z Y, LIU M, et al. Phys Rev C, 2010, 82: 044304. doi: 10.1103/PhysRevC.82.044304 [30] 圣宗强, 樊广伟, 钱建发. 物理学报, 2015, 64(11): 112101. doi: 10.7498/aps.64.112101 SHENG Z Q, FAN G W, QIAN J F. Acta Phys Sin, 2015, 64(11): 112101. (in Chinese) doi: 10.7498/aps.64.112101 [31] GORIELY S, CHAMEL N, PEARSON J M. Phys Rev C, 2013, 88: 024308. doi: 10.1103/PhysRevC.88.024308 [32] GORIELY S, CHAMEL N, PEARSON J M. Phys Rev C, 2013, 88: 061302. doi: 10.1103/PhysRevC.88.061302 [33] GORIELY S, CHAMEL N, PEARSON J M. Phys Rev C, 2016, 93: 034337. doi: 10.1103/PhysRevC.93.034337 [34] GENG L, TOKI H, MENG J. Prog Theor Phys, 2005, 113(4): 785. [35] PIEKAREWICZ J, CENTELLES M, ROCA-MAZA X, et al. Eur Phys J A, 2010, 46: 379. doi: 10.1140/epja/i2010-11051-8 [36] SUN B H, LU Y, PENG J P, et al. Phys Rev C, 2014, 90: 054318. doi: 10.1103/PhysRevC.90.054318 [37] BAO M, LU Y, ZHAO Y M, et al. Phys Rev C, 2016, 94: 064315. doi: 10.1103/PhysRevC.94.064315 [38] 庞龙刚, 周凯, 王新年. 原子核物理评论, 2020, 37(3): 720. doi: 10.11804/NuclPhysRev.37.2019CNPC41(inChinese PANG L G, ZHOU K, WANG X N. Nuclear Physics Review, 2020, 37(3): 720. (in Chinese) doi: 10.11804/NuclPhysRev.37.2019CNPC41(inChinese [39] WANG N, LIU M. Phys Rev C, 2011, 84: 051303. doi: 10.1103/PhysRevC.84.051303 [40] NIU Z M, ZHU Z L, NIU Y F, et al. Phys Rev C, 2013, 88: 024325. doi: 10.1103/PhysRevC.88.024325 [41] ZHENG J S, WANG N Y, WANG Z Y, et al. Phys Rev C, 2014, 90: 014303. doi: 10.1103/PhysRevC.90.014303 [42] NIU Z M, SUN B H, LIANG H Z, et al. Phys Rev C, 2016, 94: 054315. doi: 10.1103/PhysRevC.94.054315 [43] SHI M, NIU Z M, LIANG H Z. Chin Phys C, 2019, 43: 074104. doi: 10.1088/1674-1137/43/7/074104 [44] MA N N, BAO X J, ZHANG H F. Chin Phys C, 2021, 45: 024105. doi: 10.1088/1674-1137/45/2/abcc5c [45] NIU Z M, LIANG H Z. Phys Lett B, 2018, 778: 48. doi: 10.1016/j.physletb.2018.01.002 [46] WANG Z A, PEI J C, LIU Y, et al. Phys Rev Lett, 2019, 123: 122501. doi: 10.1103/PhysRevLett.123.122501 [47] QIAO C Y, PEI J C, WANG Z A, et al. Phys Rev C, 2021, 103: 034621. doi: 10.1103/PhysRevC.103.034621 [48] RODRÍGUEZ U B, VARGAS C Z. J Phys G: Nucl Part Phys, 2019, 46: 115109. doi: 10.1088/1361-6471/ab2c86 [49] XU J, XIE W, LI B A. Phys Rev C, 2020, 102: 044316. doi: 10.1103/PhysRevC.102.044316 [50] YANG L, LIN C J, ZHANG Y X, et al. Phys Lett B, 2020, 807: 135540. doi: 10.1016/j.physletb.2020.135540 [51] WU X H, ZHAO P W. Phys Rev C, 2020, 101: 051301. doi: 10.1103/PhysRevC.101.051301 [52] WU X H, GUO L H, ZHAO P W. Phys Lett B, 2021, 819: 136387. doi: 10.1016/j.physletb.2021.136387 [53] KOSZORÚS Á, YANG X F, JIANG W G, et al. Nat Phys, 2021, 17: 439. doi: 10.1038/s41567-020-01136-5 [54] GELDHOF S. Developments for High-Resolution Laser Spectroscopy and Application to Palladium Isotopes[D]. Jyväskylä: University of Jyväskylä, 2020: 59. [55] VERNON A R. Collinear Resonance Ionization Spectroscopy of Neutron-Rich Indium Isotopes[D]. Manchester: University of Manchester, 2019: 147. [56] CHOI H, HIRAYAMA Y, CHOI S, et al. Phys Rev C, 2020, 102: 034309. doi: 10.1103/PhysRevC.102.034309 [57] MUKAI M, HIRAYAMA Y, WATANABE Y X, et al. Phys Rev C, 2020, 102: 054307. doi: 10.1103/PhysRevC.102.054307 [58] DAY GOODACRE T, AFANASJEV A V, BARZAKH A E, et al. Phys Rev Lett, 2021, 126: 032502. doi: 10.1103/PhysRevLett.126.032502 -
点击查看大图
图(4) / 表 (1)
计量
- 文章访问数: 482
- HTML全文浏览量: 121
- PDF下载量: 334
- 被引次数: 0
甘公网安备 62010202000723号